2022~2023学年沪科版数学七年级上册期末考试试卷（一）

试卷更新日期：2023-01-03 类型：期末考试

进入出卷网下载

一、单选题（每题4分，共40分）

1. 下列说法中正确的个数为（）
①符号不同的两个数互为相反数；
②倒数等于它本身的数是±1，任何有理数都有倒数；
③绝对值等于它本身的数是正数和0；
④所有的有理数都能用数轴上的点表示．

A、1个 B、2个 C、3个 D、4个

查看试题解析
2. 下列说法正确的是（）

A、3a-5的项是3a，5 B、 $2 x^{2} y + x y^{2} + z^{2}$ 是二次三项式 C、 $2 x^{2} y$ 与 $- 5 y x^{2}$ 是同类项 D、单项式 $- 3 π y x^{2}$ 的系数是-3

查看试题解析
3. 我国领土辽阔广大，陆地总面积约为 $9600000 k m^{2}$ ，位居世界第三，仅次于俄罗斯和加拿大，用科学记数法表示 $9600000$ ，正确的选项是（）

A、 $96 \times 1 0^{5}$ B、 $9.6 \times 1 0^{5}$ C、 $9.6 \times 1 0^{6}$ D、 $0.96 \times 1 0^{7}$

查看试题解析
4. 设a，b互为相反数，c，d互为倒数，则 $2022 a - \frac{21}{c d} + 2022 b$ 的值是（）

A、2001 B、4023 C、-21 D、21

查看试题解析
5. 下列四个图中，能用∠1、∠AOB、∠O三种方法表示同一个角的是（）

A、 B、 C、 D、

查看试题解析
6. 下列各式中不能表示图中阴影部分面积的是（）

A、 $3 (x + 2) + x^{2}$ B、 $x^{2} + 5 x$ C、 $(x + 3) (x + 2) - 2 x$ D、 $x (x + 3) + 6$

查看试题解析
7. 一文具店的装订机的价格比文具盒的价格的3倍少1元，购买2把装订机和6个文具盒共需70元，问装订机与文具盒价格各是多少元？设文具盒的价格为x元，装订机的价格为y元，依题意可列方程组为（　　）

A、 $\{\begin{matrix} 3 x - y = 1 \\ 6 x + 2 y = 70 \end{matrix}$ B、 $\{\begin{matrix} y - 3 x = 1 \\ 6 x + 2 y = 70 \end{matrix}$ C、 $\{\begin{matrix} y - 3 x = 1 \\ 2 x + 6 y = 70 \end{matrix}$ D、 $\{\begin{matrix} 3 x - y = 1 \\ 2 x + 6 y = 70 \end{matrix}$

查看试题解析
8. 下列调查方式合适的是（）

A、为了解市民对电影《平凡英雄》的感受，小明在某校随机采访了8名初三学生 B、为了解全校学生国庆节假期做实践作业的时间，小莹同学在网上向3位好友做了调查 C、为了解全国青少年儿童的睡眠时间，统计人员采用了普查的方式 D、为了解“神舟十四号”载人飞船发射前零部件的状况，检测人员采用了普查的方式

查看试题解析
9. 如图，把 $△ A B C$ 沿EF翻折，叠合后的图形如图，若 $∠ A = 60 °$ ， $∠ 1 = 95 °$ ，则 $∠ 2$ 的度数是（）

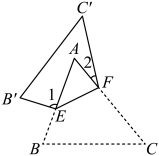A、15° B、20° C、25° D、35°

查看试题解析
10. 按照如图所示的方法排列黑色小正方形地砖，则第14个图案中黑色小正方形地砖的数量是（）

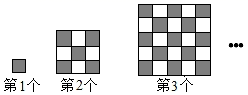A、360 B、363 C、365 D、369

查看试题解析

二、填空题（每题5分，共25分）

11. 近似数3.06×10⁴精确到位．

查看试题解析
12. 已知单项式 $2 a^{m} b$ 与 $\frac{1}{2} a^{2} b^{n + 2}$ 是同类项，那么 $m^{n} =$ ．

查看试题解析
13. 有理数a，b，c在数轴上对应的点如下图所示，则下列结论：

①a＞b；②|b+c|＝b+c；③|a－c|＝c－a；④－b＜c＜－a．

其中正确的是．（只填序号）

查看试题解析
14. 时钟在14点30分时，这时刻钟面上时针与分针夹角的度数为．

查看试题解析
15. 对于两个数a，b，我们规定用 $M {a ， b}$ 表示这两个数的平均数，用 $m i n {a ， b}$ 表示这两个数中最小的数，例如： $M {- 1 ， 2} = \frac{- 1 + 2}{2} = \frac{1}{2}$ ， $m i n {- 1 ， 2} = - 1$ ，如果 $M {3 ， 2 x + 3} = m i n {2 ， 3}$ ，那么 $x =$ ．

查看试题解析

三、计算题（共2题，共19分）

16. 计算

(1)、 $7 \frac{1}{9} \times (1 \frac{1}{2} - 1 \frac{1}{8} + 3 \frac{1}{4}) \times (- 2 \frac{1}{4})$

(2)、 $- 1^{4} + (1 - 0.5) \times \frac{1}{3} \times [2 - {(- 3)}^{2}]$

(3)、 $80 ° 1 0^{'} 3 5^{″} - 15 ° 2 8^{'} 2 5^{″} \times 3$

查看试题解析
17. 如图，∠AOB=120°，OC、OE、OF是∠AOB内的三条射线，且∠COE=60°，OF平分∠AOE，∠COF=20°，求∠BOE的度数．

查看试题解析

四、综合题（共6题，共66分）

18. 化简

(1)、已知多项式： $A = a^{2} - b^{2}$ ， $B = 2 a^{2} - 3 b^{2}$ ，求 $3 A - B$ ；

(2)、先化简，再求值： $(4 a - 5 b) - (8 a - 7 b)$ ，其中 $a = - 1 ， b = 1$ ．

查看试题解析
19. 如图，线段AB，C是线段AB上一点，M是AB的中点，N是AC的中点．

(1)、若AB＝8cm，AC＝3.2cm，求线段MN的长；

(2)、若BC＝a，试用含a的式子表示线段MN的长．

查看试题解析
20. 已知方程 $3 (x - \frac{1}{3}) = 2 x + 7$ 与关于 x 的方程3a-8=2（x+a）-a的解相同．

(1)、求 a 的值；

(2)、若 a、b在数轴上对应的点在原点的两侧，且到原点的距离相等，c 是倒数等于本身的数，求（a + b - c）²⁰²²的值．

查看试题解析
21. 某校为了了解本校七年级学生课外阅读的喜好，随机抽取该校七年级部分学生进行问卷调查（每人只选一种书籍）．下图是整理数据后绘制的两幅不完整的统计图，请你根据图中提供的信息解答下列问题：

(1)、这次活动一共调查了名学生；

(2)、在扇形统计图中，“其他”所在扇形的圆心角等于度；

(3)、补全条形统计图；

(4)、若该年级有600名学生，请你估计该年级喜欢“科普常识”的学生人数约是．

查看试题解析
22. 卡塔尔世界杯正在火热进行中，在购买足球赛门票时，设购买门票张数为 a（张），现有两种购买方案：方案一：若单位赞助广告费 10000 元，则该单位购买门票的价格为60元（总费用＝广告赞助费+门票费）．方案二：若购买的门票数不超过 100 张，每张 100 元，若所购门票超过 100 张，则超出部分按八折计算．解答下列问题：

(1)、方案一中，用含 a 的代数式来表示总费用为．方案二中，当购买的门票数 a 不超过 100 张时，用含 x 的代数式来表示总费用为 .当所购门票数 a 超过 100 张时，用含 x 的代数式来表示总费用为．

(2)、甲、乙两单位分别采用方案一、方案二购买本次足球赛门票，合计 700 张，花去的总费用计 58000元，求甲、乙两单位各购买门票多少张？

查看试题解析
23. 已知点M在数轴上对应的数为a，点N在数轴上对应的数为b，M、N之间的距离记为 $| M N | = | a - b | 或 | b - a |$ ，请回答下列问题：

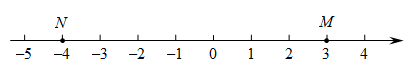(1)、如图：当 $a = 3 ， b = - 4$ 时， $| M N | =$ ；

(2)、在（1）的条件下，动点P表示的数为y，若点P在点M，N之间，则 $| y - 3 | + | y + 4 | =$ ；

(3)、在（1）的条件下，若点P表示的数是-8，现有一虫子从点P出发，以每秒1个单位长度的速度向右运动，当经过多少秒时，虫子所在的点到点M，点N的距离之和是10？

查看试题解析