2023年中考数学精选真题实战测试5 因式分解A

试卷更新日期：2023-01-03 类型：二轮复习

进入出卷网下载

一、单选题（每题3分，共30分）

1. 下面各式从左到右的变形，属于因式分解的是（）

A、 $x^{2} - x - 1 = x (x - 1) - 1$ B、 $x^{2} - 1 = (x - 1)^{2}$ C、 $x^{2} - x - 6 = (x - 3) (x + 2)$ D、 $x (x - 1) = x^{2} - x$

查看试题解析
2. 因式分解： $x^{3} - 4 x =$ （）

A、 $x (x^{2} - 4 x)$ B、 $x (x + 4) (x - 4)$ C、 $x (x + 2) (x - 2)$ D、 $x (x^{2} - 4)$

查看试题解析
3. 把多项式 $a^{2} + 2 a$ 分解因式得（）

A、 $a (a + 2)$ B、 $a (a - 2)$ C、 ${(a + 2)}^{2}$ D、 $(a + 2) (a - 2)$

查看试题解析
4. 多项式 $x^{2} ﹣ 4 x + 4$ 因式分解的结果是（）

A、x（x﹣4）+4 B、（x+2）（x﹣2） C、（x+2）² D、（x﹣2）²

查看试题解析
5. 多项式 $39 x^{2} + 5 x - 14$ 可因式分解成 $(3 x + a) (b x + c)$ ，其中 $a$ 、 $b$ 、 $c$ 均为整数，求 $a + 2 c$ 之值为何？（）

A、-12 B、-3 C、3 D、12

查看试题解析
6. 下列因式分解正确的是（）

A、 $a x + a y = a (x + y) + 1$ B、 $3 a + 3 b = 3 (a + b)$ C、 $a^{2} + 4 a + 4 = {(a + 4)}^{2}$ D、 $a^{2} + b = a (a + b)$

查看试题解析
7. 图2是图1中长方体的三视图，若用S表示面积，S_主＝x²+2x ， S_左＝x²+x ，则S_俯＝（）

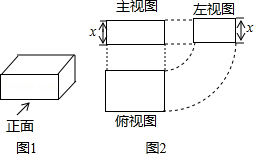A、x²+3x+2 B、x²+2 C、x²+2x+1 D、2x²+3x

查看试题解析
8. 对于① $x - 3 x y = x (1 - 3 y)$ ，② $(x + 3) (x - 1) = x^{2} + 2 x - 3$ ，从左到右的变形，表述正确的是（）

A、都是因式分解 B、都是乘法运算 C、①是因式分解，②是乘法运算 D、①是乘法运算，②是因式分解

查看试题解析
9. 下列多项式中，能用平方差公式进行因式分解的是（）

A、a²﹣b² B、﹣a²﹣b² C、a²+b² D、a²+2ab+b²

查看试题解析
10. 如果 $m + n = 1$ ，那么代数式 $(\frac{2 m + n}{m^{2} - m n} + \frac{1}{m}) \cdot (m^{2} - n^{2})$ 的值为（）

A、-3 B、-1 C、1 D、3

查看试题解析

二、填空题（每空3分，共18分）

11. 因式分解： $a^{2} - 16 =$ ．

查看试题解析
12. 分解因式： $3 a^{2} - 21 a b =$

查看试题解析
13. 已知m，n同时满足2m+n＝3与2m﹣n＝1，则4m²﹣n²的值是．

查看试题解析
14. 已知 $a b = 2$ ， $a + b = 3$ ，则 $a^{2} b + a b^{2}$ 的值为．

查看试题解析
15. 分解因式： $2022 x^{2} - 4044 x + 2022 =$ .

查看试题解析
16. 已知 $m^{2} + n^{2} + 10 = 6 m - 2 n$ ，则 $m - n =$ .

查看试题解析

三、解答题（共9题，共72分）

17. 因式分解：mx²﹣my² ．

查看试题解析
18. 分解因式：（x-1）²+2（x-5）.

查看试题解析
19. 已知 $x - y = 2 ， \frac{1}{x} - \frac{1}{y} = 1$ ，求 $x^{2} y - x y^{2}$ 的值.

查看试题解析
20. 已知非零实数a，b满足a+b=3， $\frac{1}{a}$ + $\frac{1}{b}$ = $\frac{3}{2}$ ，求代数式a²b+ab²的值．

查看试题解析
21. 阅读材料：运用公式法分解因式，除了常用的平方差公式和完全平方公式以外，还可以应用其他公式，如立方和与立方差公式，其公式如下：
立方和公式： $x^{3} + y^{3} = (x + y) (x^{2} - x y + y^{2})$ ；

立方差公式： $x^{3} - y^{3} = (x - y) (x^{2} + x y + y^{2})$ ；

根据材料和已学知识，先化简，再求值： $\frac{3 x}{x^{2} - 2 x} - \frac{x^{2} + 2 x + 4}{x^{3} - 8}$ ，其中 $x = 3$ ．

查看试题解析
22. 如图，学校劳动实践基地有两块边长分别为 $a$ ， $b$ 的正方形秧田 $A$ ， $B$ ，其中不能使用的面积为 $M$ ．

(1)、用含 $a$ ， $M$ 的代数式表示 $A$ 中能使用的面积；

(2)、若 $a + b = 10$ ， $a - b = 5$ ，求 $A$ 比 $B$ 多出的使用面积．

查看试题解析
23. 我们知道，任意一个正整数n都可以进行这样的分解：n=p×q（p，q是正整数，且p≤q），在n的所有这种分解中，如果p，q两因数之差的绝对值最小，我们就称p×q是n的最佳分解．并规定：F（n）= $\frac{p}{q}$ ．
例如12可以分解成1×12，2×6或3×4，因为12﹣1＞6﹣2＞4﹣3，所以3×4是12的最佳分解，所以F（12）= $\frac{3}{4}$ ．
（Ⅰ）如果一个正整数m是另外一个正整数n的平方，我们称正整数m是完全平方数．
求证：对任意一个完全平方数m，总有F（m）=1；
（Ⅱ）如果一个两位正整数t，t=10x+y（1≤x≤y≤9，x，y为自然数），交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差为36，那么我们称这个数t为“吉祥数”，求所有“吉祥数”；
（Ⅲ）在（2）所得“吉祥数”中，求F（t）的最大值．

查看试题解析
24. 发现任意五个连续整数的平方和是5的倍数．

(1)、验证
①（﹣1）²+0²+1²+2²+3²的结果是5的几倍？
②设五个连续整数的中间一个为n，写出它们的平方和，并说明是5的倍数．

(2)、延伸
任意三个连续整数的平方和被3除的余数是几呢？请写出理由．

查看试题解析
25. 八年级课外兴趣小组活动时，老师提出了如下问题：
将 $2 a - 3 a b - 4 + 6 b$ 因式分解．
【观察】经过小组合作交流，小明得到了如下的解决方法：
解法一：原式 $= (2 a - 3 a b) - (4 - 6 b) = a (2 - 3 b) - 2 (2 - 3 b) = (2 - 3 b) (a - 2)$
解法二：原式 $= (2 a - 4) - (3 a b - 6 b) = 2 (a - 2) - 3 b (a - 2) = (a - 2) (2 - 3 b)$
【感悟】对项数较多的多项式无法直接进行因式分解时，我们可以将多项式分为若干组，再利用提公因式法、公式法达到因式分解的目的，这就是因式分解的分组分解法．分组分解法在代数式的化简、求值及方程、函数等学习中起着重要的作用．（温馨提示：因式分解一定要分解到不能再分解为止）

(1)、【类比】
请用分组分解法将 $x^{2} - a^{2} + x + a$ 因式分解；

(2)、【挑战】
请用分组分解法将 $a x + a^{2} - 2 a b - b x + b^{2}$ 因式分解；

(3)、【应用】
“赵爽弦图”是我国古代数学的骄傲，我们利用它验证了勾股定理．如图，“赵爽弦图”是由四个全等的直角三角形围成的一个大正方形，中间是一个小正方形．若直角三角形的两条直角边长分别是a和 $b (a > b)$ ，斜边长是3，小正方形的面积是1．根据以上信息，先将 $a^{4} - 2 a^{3} b + 2 a^{2} b^{2} - 2 a b^{3} + b^{4}$ 因式分解，再求值．

查看试题解析