2012年高考理数真题试卷（四川卷）

试卷更新日期：2016-09-26 类型：高考真卷

进入出卷网下载

一、选择题：每小题给出的四个选项中，只有一项是符合题目要求的．

1. （1+x）⁷的展开式中x²的系数是（）

A、42 B、35 C、28 D、21

查看试题解析
2. 复数 $\frac{{(1 - i)}^{2}}{2 i}$ =（）

A、1 B、﹣1 C、i D、﹣i

查看试题解析
3. 函数 $f (x) = {\begin{matrix} \frac{x^{2} - 9}{x - 3} ， x < 3 \\ \ln (x - 2) ， x \geq 3 \end{matrix}$ 在x=3处的极限是（）

A、不存在 B、等于6 C、等于3 D、等于0

查看试题解析
4.
如图，正方形ABCD的边长为1，延长BA至E，使AE=1，连接EC、ED则sin∠CED=（）

A、 $\frac{3 \sqrt{10}}{10}$ B、 $\frac{\sqrt{10}}{10}$ C、 $\frac{\sqrt{5}}{10}$ D、 $\frac{\sqrt{5}}{15}$

查看试题解析
5. 函数y=a^x﹣ $\frac{1}{a}$ （a＞0，a≠1）的图象可能是（）

A、 B、 C、 D、

查看试题解析
6. 下列命题正确的是（）

A、若两条直线和同一个平面所成的角相等，则这两条直线平行 B、若一个平面内有三个点到另一个平面的距离相等，则这两个平面平行 C、若一条直线平行于两个相交平面，则这条直线与这两个平面的交线平行 D、若两个平面都垂直于第三个平面，则这两个平面平行

查看试题解析
7. 设 $\vec{a}$ 、 $\vec{b}$ 都是非零向量，下列四个条件中，使 $\frac{\vec{a}}{| \vec{a} |} = \frac{\vec{b}}{| \vec{b} |}$ 成立的充分条件是（）

A、 $\vec{a} = - \vec{b}$ B、 $\vec{a} ∥ \vec{b}$ C、 $\vec{a} = 2 \vec{b}$ D、 $\vec{a} ∥ \vec{b}$ 且 $| \vec{a} | = | \vec{b} |$

查看试题解析
8. 已知抛物线关于x轴对称，它的顶点在坐标原点O，并且经过点M（2，y₀）．若点M到该抛物线焦点的距离为3，则|OM|=（）

A、 $2 \sqrt{2}$ B、 $2 \sqrt{3}$ C、4 D、 $2 \sqrt{5}$

查看试题解析
9. 某公司生产甲、乙两种桶装产品．已知生产甲产品1桶需耗A原料1千克、B原料2千克；生产乙产品1桶需耗A原料2千克，B原料1千克．每桶甲产品的利润是300元，每桶乙产品的利润是400元．公司在生产这两种产品的计划中，要求每天消耗A、B原料都不超过12千克．通过合理安排生产计划，从每天生产的甲、乙两种产品中，公司共可获得的最大利润是（）

A、1800元 B、2400元 C、2800元 D、3100元

查看试题解析
10.
如图，半径为R的半球O的底面圆O在平面α内，过点O作平面α的垂线交半球面于点A，过圆O的直径CD作平面α成45°角的平面与半球面相交，所得交线上到平面α的距离最大的点为B，该交线上的一点P满足∠BOP=60°，则A、P两点间的球面距离为（）

A、 $R ar \cos \frac{\sqrt{2}}{4}$ B、 $\frac{π R}{4}$ C、 $R ar \cos \frac{\sqrt{3}}{3}$ D、 $\frac{π R}{3}$

查看试题解析
11. 方程ay=b²x²+c中的a，b，c∈{﹣3，﹣2，0，1，2，3}，且a，b，c互不相同，在所有这些方程所表示的曲线中，不同的抛物线共有（）

A、60条 B、62条 C、71条 D、80条

查看试题解析
12. 设函数f（x）=2x﹣cosx，{a_n}是公差为 $\frac{π}{8}$ 的等差数列，f（a₁）+f（a₂）+…+f（a₅）=5π，则 ${[f (a_{3})]}^{2} - a_{1} a_{3}$ =（）

A、0 B、 $\frac{1}{16} π^{2}$ C、 $\frac{1}{8} π^{2}$ D、 $\frac{13}{16} π^{2}$

查看试题解析

二、填空题（把答案填在答题纸的相应位置上．）

13. 设全集U={a，b，c，d}，集合A={a，b}，B={b，c，d}，则（∁_UA）∪（∁_UB）= ．

查看试题解析
14. 如图，在正方体ABCD﹣A₁B₁C₁D₁中，M、N分别是CD、CC₁的中点，则异面直线A₁M与DN所成的角的大小是．

查看试题解析
15. 椭圆 $\frac{x^{2}}{4} + \frac{y^{2}}{3} = 1$ 的左焦点为F，直线x=m与椭圆相交于点A、B，当△FAB的周长最大时，△FAB的面积是．

查看试题解析
16. 记[x]为不超过实数x的最大整数，例如，[2]=2，[1.5]=1，[﹣0.3]=﹣1．设a为正整数，数列{x_n}满足x₁=a， $x_{n + 1} = [\frac{x_{n} + [\frac{a}{x_{n}}]}{2}] (x \in N^{*})$ ，现有下列命题：
①当a=5时，数列{x_n}的前3项依次为5，3，2；
②对数列{x_n}都存在正整数k，当n≥k时总有x_n=x_k；
③当n≥1时， $x_{n} > \sqrt{a} - 1$ ；
④对某个正整数k，若x_k+1≥x_k ，则 $x_{k} = [\sqrt{a}]$ ．
其中的真命题有．（写出所有真命题的编号）

查看试题解析

三、解答题（解答应写出必要的文字说明，证明过程或演算步骤．）

17. 某居民小区有两个相互独立的安全防范系统（简称系统）A和B，系统A和B在任意时刻发生故障的概率分别为 $\frac{1}{10}$ 和p．

(1)、若在任意时刻至少有一个系统不发生故障的概率为 $\frac{49}{50}$ ，求p的值；

(2)、设系统A在3次相互独立的检测中不发生故障的次数为随机变量ξ，求ξ的概率分布列及数学期望Eξ．

查看试题解析
18. 函数f（x）=6cos² $\frac{ω x}{2} + \sqrt{3}$ sinωx﹣3（ω＞0）在一个周期内的图象如图所示，A为图象的最高点，B、C为图象与x轴的交点，且△ABC为正三角形．

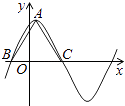(1)、求ω的值及函数f（x）的值域；

(2)、若f（x₀）= $\frac{8 \sqrt{3}}{5}$ ，且x₀∈（﹣ $\frac{10}{3} ， \frac{2}{3}$ ），求f（x₀+1）的值．

查看试题解析
19. 如图，在三棱锥P﹣ABC中，∠APB=90°，∠PAB=60°，AB=BC=CA，平面PAB⊥平面ABC．

(1)、求直线PC与平面ABC所成角的大小；

(2)、求二面角B﹣AP﹣C的大小．

查看试题解析
20. 已知数列{a_n}的前n项和为S_n ，且a₂a_n=S₂+S_n对一切正整数n都成立．

(1)、求a₁ ， a₂的值；

(2)、设a₁＞0，数列{lg $\frac{10 a_{1}}{a_{n}}$ }的前n项和为T_n ，当n为何值时，T_n最大？并求出T_n的最大值．

查看试题解析
21. 如图，动点M到两定点A（﹣1，0）、B（2，0）构成△MAB，且∠MBA=2∠MAB，设动点M的轨迹为C．

(1)、求轨迹C的方程；

(2)、设直线y=﹣2x+m与y轴交于点P，与轨迹C相交于点Q、R，且|PQ|＜|PR|，求 $\frac{| P R |}{| P Q |}$ 的取值范围．

查看试题解析
22. 已知a为正实数，n为自然数，抛物线 $y = - x^{2} + \frac{a^{n}}{2}$ 与x轴正半轴相交于点A，设f（n）为该抛物线在点A处的切线在y轴上的截距．

(1)、用a和n表示f（n）；

(2)、求对所有n都有 $\frac{f (n) - 1}{f (n) + 1} \geq \frac{n^{3}}{n^{3} + 1}$ 成立的a的最小值；

(3)、当0＜a＜1时，比较 $\sum_{k = 1}^{n} \frac{1}{f (k) - f (2 k)}$ 与 $\frac{27}{4} \cdot \frac{f (1) - f (n)}{f (0) - f (1)}$ 的大小，并说明理由．

查看试题解析