2023年中考数学精选真题实战测试4 整式B

试卷更新日期：2023-01-02 类型：二轮复习

进入出卷网下载

一、单选题（每题3分，共30分）

1. 为落实“双减”政策，某校利用课后服务开展了主题为“书香满校园”的读书活动.现需购买甲，乙两种读本共100本供学生阅读，其中甲种读本的单价为10元/本，乙种读本的单价为8元/本，设购买甲种读本x本，则购买乙种读本的费用为（）

A、 $8 x$ 元 B、 $10 (100 - x)$ 元 C、 $8 (100 - x)$ 元 D、 $(100 - 8 x)$ 元

查看试题解析
2. 生物学中，描述、解释和预测种群数量的变化，常常需要建立数学模型.在营养和生存空间没有限制的情况下，某种细胞可通过分裂来繁殖后代，我们就用数学模型2ⁿ来表示.即：2¹＝2，2²＝4，2³＝8，2⁴＝16，2⁵＝32，……，请你推算2²⁰²²的个位数字是（）

A、8 B、6 C、4 D、2

查看试题解析
3. 下列运算正确的是（）

A、 $\sqrt{(- 2)^{2}} = - 2$ B、 ${(\frac{1}{3})}^{- 1} = - \frac{1}{3}$ C、 ${(a^{2})}^{3} = a^{6}$ D、 $a^{8} \div a^{4} = a^{2} (a \neq 0)$

查看试题解析
4. 下列计算正确的是（）

A、 $2 a + 3 b = 5 a b$ B、 $(a + b)^{2} = a^{2} + b^{2}$ C、 $a^{2} \times a = a^{3}$ D、 ${(a^{2})}^{3} = a^{5}$

查看试题解析
5. 下列运算正确的是（）

A、3a²﹣a²＝3 B、a³÷a²＝a C、（﹣3ab²）²＝﹣6a²b⁴ D、（a+b）²＝a²+ab+b²

查看试题解析
6. 已知实数a，b满足 $b - a = 1$ ，则代数式 $a^{2} + 2 b - 6 a + 7$ 的最小值等于（）

A、5 B、4 C、3 D、2

查看试题解析
7. 下列运算正确的是（）

A、 $\sqrt{\frac{1}{2}} \times \sqrt{8} = \pm 2$ B、 $(m + n)^{2} = m^{2} + n^{2}$ C、 $\frac{1}{x - 1} - \frac{2}{x} = - \frac{1}{x}$ D、 $3 x y \div \frac{- 2 y^{2}}{3 x} = - \frac{9 x^{2}}{2 y}$

查看试题解析
8. 已知 $(x + 2) (x - 2) - 2 x = 1$ ，则 $2 x^{2} - 4 x + 3$ 的值为（）

A、13 B、8 C、－3 D、5

查看试题解析
9. 若 $1 0^{x} = N$ ，则称 $x$ 是以10为底 $N$ 的对数.记作： $x = l g N$ .例如： $1 0^{2} = 100$ ，则 $2 = l g 100$ ； $1 0^{0} = 1$ ，则 $0 = l g 1$ .对数运算满足：当 $M > 0$ ， $N > 0$ 时， $l g M + l g N = l g (M N)$ ，例如： $l g 3 + l g 5 = l g 15$ ，则 ${(l g 5)}^{2} + l g 5 \times l g 2 + l g 2$ 的值为（）

A、5 B、2 C、1 D、0

查看试题解析
10. 如图，已知矩形ABCD的边长分别为a，b，进行如下操作：第一次，顺次连接矩形ABCD各边的中点，得到四边形 $A_{1} B_{1} C_{1} D_{1}$ ；第二次，顺次连接四边形 $A_{1} B_{1} C_{1} D_{1}$ 各边的中点，得到四边形 $A_{2} B_{2} C_{2} D_{2}$ ；…如此反复操作下去，则第n次操作后，得到四边形 $A_{n} B_{n} C_{n} D_{n}$ 的面积是（）

A、 $\frac{a b}{2^{n}}$ B、 $\frac{a b}{2^{n - 1}}$ C、 $\frac{a b}{2^{n + 1}}$ D、 $\frac{a b}{2^{2 n}}$

查看试题解析

二、填空题（每空3分，共21分）

11. 规定：在平面直角坐标系中，一个点作“0”变换表示将它向右平移一个单位，一个点作“1”变换表示将它绕原点顺时针旋转90°，由数字0和1组成的序列表示一个点按照上面描述依次连续变换．例如：如图，点 $O (0 ， 0)$ 按序列“011…”作变换，表示点O先向右平移一个单位得到 $O_{1} (1 ， 0)$ ，再将 $O_{1} (1 ， 0)$ 绕原点顺时针旋转90°得到 $O_{2} (0 ， - 1)$ ，再将 $O_{2} (0 ， - 1)$ 绕原点顺时针旋转90°得到 $O_{3} (- 1 ， 0)$ …依次类推．点 $(0 ， 1)$ 经过“011011011”变换后得到点的坐标为．

查看试题解析
12. 若一个多项式加上 $3 x y + 2 y^{2} - 8$ ，结果得 $2 x y + 3 y^{2} - 5$ ，则这个多项式为．

查看试题解析
13. 如图，某链条每节长为 $2.8 cm$ ，每两节链条相连接部分重叠的圆的直径为 $1 cm$ ，按这种连接方式，50节链条总长度为 $cm$ .

查看试题解析
14. 已知 $x + y = 4$ ， $x - y = 6$ ，则 $x^{2} - y^{2} =$ .

查看试题解析
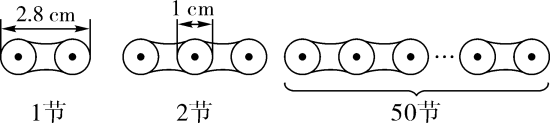15. 正偶数2，4，6，8，10，…，按如下规律排列，
则第27行的第21个数是 .

查看试题解析
16. 观察下列一组数：2， $\frac{1}{2}$ ， $\frac{2}{7}$ ， …，它们按一定规律排列，第n个数记为 $a_{n}$ ，且满足 $\frac{1}{a_{n}} + \frac{1}{a_{n + 2}} = \frac{2}{a_{n + 1}}$ .则 $a_{4} =$ ， $a_{2022} =$ .

查看试题解析

三、解答题（共8题，共69分）

17. 先化简，再求值：4xy－2xy－（－3xy），其中x＝2，y＝－1.

查看试题解析
18. 先化简，再求值：（1+x）（1﹣x）+x（x+2），其中x = $\frac{1}{2}$ ．

查看试题解析
19. 先化简，再求值：（x+1）²+（2+x）（2﹣x），其中x＝1.

查看试题解析
20. 观察下面的等式： $\frac{1}{2} = \frac{1}{3} + \frac{1}{6}$ ， $\frac{1}{3} = \frac{1}{4} + \frac{1}{12}$ ， $\frac{1}{4} = \frac{1}{5} + \frac{1}{20}$ ，……

(1)、按上面的规律归纳出一个一般的结论(用含n的等式表示，n为正整数)．

(2)、请运用分式的有关知识，推理说明这个结论是正确的。

查看试题解析
21. 对于一个各数位上的数字均不为 0 的三位自然数 N，若 N 能被它的各数位上的数字之和 m 整除，则称 N 是 m 的“和倍数”．
例如：∵247÷(2+4+7)= 247÷13=19，∴247是13的“和倍数”.

又如： ∵214÷(2+1+4)=214÷7=30……4，∴214不是“和倍数”.

(1)、判断 357，441 是否是“和倍数”？说明理由；

(2)、三位数 A是12的“和倍数”，a，b，c 分别是数 A其中一个数位上的数字，且 a>b>c在 a，b，c 中任选两个组成两位数，其中最大的两位数记为 F (A)，最小的两位数记为 G(A)，若 $\frac{F (A) + G (A)}{16}$ 为整数，求出满足条件的所有数 A．

查看试题解析
22. 设 $\bar{a 5}$ 是一个两位数，其中a是十位上的数字（1≤a≤9）．例如，当a＝4时， $\bar{a 5}$ 表示的两位数是45．

(1)、尝试：
①当a＝1时，15²＝225＝1×2×100＋25；

②当a＝2时，25²＝625＝2×3×100＋25；

③当a＝3时，35²＝1225＝；

……

(2)、归纳： ${\bar{a 5}}^{2}$ 与100a(a＋1)＋25有怎样的大小关系？试说明理由．

(3)、运用：若 ${\bar{a 5}}^{2}$ 与100a的差为2525，求a的值．

查看试题解析
23. 若关于x的函数y，当 $t - \frac{1}{2} \leq x \leq t + \frac{1}{2}$ 时，函数y的最大值为M，最小值为N，令函数 $h = \frac{M - N}{2}$ ，我们不妨把函数h称之为函数y的“共同体函数”.

(1)、①若函数 $y = 4044 x$ ，当 $t = 1$ 时，求函数y的“共同体函数”h的值；
②若函数 $y = k x + b$ （ $k \neq 0$ ， k，b为常数），求函数y的“共同体函数”h的解析式；

(2)、若函数 $y = \frac{2}{x} （ x \geq 1 ）$ ，求函数y的“共同体函数”h的最大值；

(3)、若函数 $y = - x^{2} + 4 x + k$ ，是否存在实数k，使得函数y的最大值等于函数y的“共同体函数”h的最小值.若存在，求出k的值；若不存在，请说明理由.

查看试题解析

24. 问题提出：

最长边长为128的整数边三角形有多少个？（整数边三角形是指三边长度都是整数的三角形．）

问题探究：

为了探究规律，我们先从最简单的情形入手，从中找到解决问题的方法，最后得出一般性的结论．

①如表①，最长边长为1的整数边三角形，显然，最短边长是1，第三边长也是1.按照（最长边长，最短边长，第三边长）的形式记为 $(1 ， 1 ， 1)$ ，有1个，所以总共有 $1 \times 1 = 1$ 个整数边三角形．

表①

最长边长	最短边长	（最长边长，最短边长，第三边长）	整数边三角形个数	计算方法	算式
1	1	$(1 ， 1 ， 1)$	1	1个1	$1 \times 1$

②如表②，最长边长为2的整数边三角形，最短边长是1或2.根据三角形任意两边之和大于第三边，当最短边长为1时，第三边长只能是2，记为 $(2 ， 1 ， 2)$ ，有1个；当最短边长为2时，显然第三边长也是2，记为 $(2 ， 2 ， 2)$ ，有1个，所以总共有 $1 + 1 = 1 \times 2 = 2$ 个整数边三角形．

表②

最长边长	最短边长	（最长边长，最短边长，第三边长）	整数边三角形个数	计算方法	算式
2	1	$(2 ， 1 ， 2)$	1	2个1	$1 \times 2$
2	2	$(2 ， 2 ， 2)$	1	2个1	$1 \times 2$

③下面在表③中总结最长边长为3的整数边三角形个数情况：

表③

最长边长	最短边长	（最长边长，最短边长，第三边长）	整数边三角形个数	计算方法	算式
3	1	$(3 ， 1 ， 3)$	1	2个2	$2 \times 2$
	2	$(3 ， 2 ， 2)$ ， $(3 ， 2 ， 3)$	2
	3	$(3 ， 3 ， 3)$	1

④下面在表④中总结最长边长为4的整数边三角形个数情况：

表④

最长边长	最短边长	（最长边长，最短边长，第三边长）	整数边三角形个数	计算方法	算式
4	1	$(4 ， 1 ， 4)$	1	3个2	$2 \times 3$
	2	$(4 ， 2 ， 3)$ ， $(4 ， 2 ， 4)$	2
	3	$(4 ， 3 ， 3)$ ， $(4 ， 3 ， 4)$	2
	4	$(4 ， 4 ， 4)$	1

(1)、请在表⑤中总结最长边长为5的整数边三角形个数情况并填空：

表⑤

最长边长	最短边长	（最长边长，最短边长，第三边长）	整数边三角形个数	计算方法	算式
5	1	$(5 ， 1 ， 5)$	1	.......	.......
	2	$(5 ， 2 ， 4)$ ， $(5 ， 2 ， 5)$	2
	3	......	......
	4	$(5 ， 4 ， 4)$ ， $(5 ， 4 ， 5)$	2
	5	$(5 ， 5 ， 5)$	1

(2)、问题解决：

最长边长为6的整数边三角形有个．

(3)、在整数边三角形中，设最长边长为

n

，总结上述探究过程，当

n

为奇数或

n

为偶数时，整数边三角形个数的规律一样吗？请写出最长边长为

n

的整数边三角形的个数．

(4)、最长边长为128的整数边三角形有个．

(5)、拓展延伸：

在直三棱柱中，若所有棱长均为整数，则最长棱长为9的直三棱柱有个．

查看试题解析