2023年中考数学精选真题实战测试3 整式A

试卷更新日期：2023-01-02 类型：二轮复习

进入出卷网下载

一、单选题（每题2分，共20分）

1. 计算 $a^{2} \cdot a^{3}$ ，结果正确的是（）

A、 $a^{2}$ B、 $a^{3}$ C、 $a^{5}$ D、 $a^{6}$

查看试题解析
2. 下列计算正确的是（）

A、2ab﹣ab＝ab B、2ab+ab＝2a²b² C、4a³b²﹣2a＝2a²b D、﹣2ab²﹣a²b＝﹣3a²b²

查看试题解析
3. 计算： ${(x + 2 y)}^{2} =$ （）

A、 $x^{2} + 4 x y + 4 y^{2}$ B、 $x^{2} + 2 x y + 4 y^{2}$ C、 $x^{2} + 4 x y + 2 y^{2}$ D、 $x^{2} + 4 x^{2}$

查看试题解析
4. 如图，是利用割补法求图形面积的示意图，下列公式中与之相对应的是（）

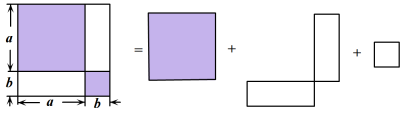A、 $(a + b)^{2} = a^{2} + 2 a b + b^{2}$ B、 $(a - b)^{2} = a^{2} - 2 a b + b^{2}$ C、 $(a + b) (a - b) = a^{2} - b^{2}$ D、 $(a b)^{2} = a^{2} b^{2}$

查看试题解析
5. 按一定规律排列的一组数据： $\frac{1}{2}$ ， $- \frac{3}{5}$ ， $\frac{1}{2}$ ， $- \frac{7}{17}$ ， $\frac{9}{26}$ ， $- \frac{11}{37}$ ， …．则按此规律排列的第10个数是（）

A、 $- \frac{19}{101}$ B、 $\frac{21}{101}$ C、 $- \frac{19}{82}$ D、 $\frac{21}{82}$

查看试题解析
6. 已知实数m，n满足 $m^{2} + n^{2} = 2 + m n$ ，则 ${(2 m - 3 n)}^{2} + (m + 2 n) (m - 2 n)$ 的最大值为（）

A、24 B、 $\frac{44}{3}$ C、 $\frac{16}{3}$ D、-4

查看试题解析
7. 已知 ${(x + y)}^{4} = a_{1} x^{4} + a_{2} x^{3} y + a_{3} x^{2} y^{2} + a_{4} x y^{3} + a_{5} y^{4}$ ，则 $a_{1} + a_{2} + a_{3} + a_{4} + a_{5}$ 的值是（）

A、4 B、8 C、16 D、12

查看试题解析
8. 已知 $x_{1}$ ， $x_{2}$ 是方程 $x^{2} - x - 2022 = 0$ 的两个实数根，则代数式 $x_{1}^{3} - 2022 x_{1} + x_{2}^{2}$ 的值是（）

A、4045 B、4044 C、2022 D、1

查看试题解析
9. 若 $2^{4} \times 2^{2} = 2^{m}$ ，则m的值为（）

A、8 B、6 C、5 D、2

查看试题解析
10. 如图，用相同的圆点按照一定的规律拼出图形．第一幅图4个圆点，第二幅图7个圆点，第三幅图10个圆点，第四幅图13个圆点……按照此规律，第一百幅图中圆点的个数是（）

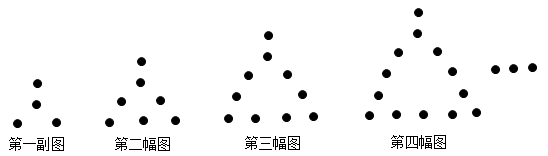A、297 B、301 C、303 D、400

查看试题解析

二、填空题（每空3分，共18分）

11. 已知a+b=1，则代数式a²﹣b² +2b+9的值为.

查看试题解析
12. 按一定规律排列的数据依次为 $\frac{1}{2}$ ， $\frac{4}{5}$ ， $\frac{7}{10}$ ， $\frac{10}{17}$ ……按此规律排列，则第30个数是．

查看试题解析
13. 对于非零实数a，b，规定a⊕b＝ $\frac{1}{a} - \frac{1}{b}$ ，若（2x﹣1）⊕2＝1，则x的值为 .

查看试题解析
14. 在反比例函数 $y = \frac{k - 1}{x}$ 的图象的每一支上，y都随x的增大而减小，且整式 $x^{2} - k x + 4$ 是一个完全平方式，则该反比例函数的解析式为.

查看试题解析
15. 已知 $a + b = 4$ ， $a - b = 2$ ，则 $a^{2} - b^{2}$ 的值为.

查看试题解析
16. 阅读材料：整体代值是数学中常用的方法.例如“已知 $3 a - b = 2$ ，求代数式 $6 a - 2 b - 1$ 的值.”可以这样解： $6 a - 2 b - 1 = 2 (3 a - b) - 1 = 2 \times 2 - 1 = 3$ .根据阅读材料，解决问题：若 $x = 2$ 是关于x的一元一次方程 $a x + b = 3$ 的解，则代数式 $4 a^{2} + 4 a b + b^{2} + 4 a + 2 b - 1$ 的值是.

查看试题解析

三、解答题（共9题，共82分）

17. 先化简，再求值：（a+2b）²+（a+2b）（a-2b）+2a（b-a），其中a＝ $\sqrt{3}$ - $\sqrt{2}$ ， b＝ $\sqrt{3}$ + $\sqrt{2}$ ．

查看试题解析
18. 先化简，再求值： $(x + 4) (x - 4) + {(x - 3)}^{2}$ ，其中 $x^{2} - 3 x + 1 = 0$ ．

查看试题解析
19. 先化简，再求值 $x (x + y) (x - y) + (x y^{2} - 2 x y) + x$ ，其中 $x = 1 ， y = \frac{1}{2}$ .

查看试题解析
20. 先化简，再求值： $4 x y - 2 x y - (- 3 x y)$ ，其中 $x = 2$ ， $y = - 1$ .

查看试题解析
21. 如图，学校劳动实践基地有两块边长分别为 $a$ ， $b$ 的正方形秧田 $A$ ， $B$ ，其中不能使用的面积为 $M$ ．

(1)、用含 $a$ ， $M$ 的代数式表示 $A$ 中能使用的面积；

(2)、若 $a + b = 10$ ， $a - b = 5$ ，求 $A$ 比 $B$ 多出的使用面积．

查看试题解析
22. 健康生技公司培养绿藻以制作「绿藻粉」，再经过后续的加工步骤，制成绿藻相关的保健食品.已知该公司制作每1公克的「绿藻粉」需要60亿个绿藻细胞.
请根据上述信息回答下列问题，完整写出你的解题过程并详细解释：

(1)、假设在光照充沛的环境下，1个绿藻细胞每20小时可分裂成4个绿藻细胞，且分裂后的细胞亦可继续分裂.今从1个绿藻细胞开始培养，若培养期间绿藻细胞皆未死亡且培养环境的光照充沛，经过15天后，共分裂成4^k个绿藻细胞，则k之值为何？

(2)、承（1），已知60亿介于 $2^{32}$ 与 $2^{33}$ 之间，请判断4^k个绿藻细胞是否足够制作8公克的「绿藻粉」？

查看试题解析
23. 整式 $3 (\frac{1}{3} - m)$ 的值为P ．

(1)、当m＝2时，求P的值；

(2)、若P的取值范围如图所示，求m的负整数值．

查看试题解析
24. 定义：对于一次函数 $y_{1} = a x + b 、 y_{2} = c x + d$ ，我们称函数 $y = m (a x + b) + n (c x + d) (m a + n c \neq 0)$ 为函数 $y_{1} 、 y_{2}$ 的“组合函数”.

(1)、若m=3，n=1，试判断函数 $y = 5 x + 2$ 是否为函数 $y_{1} = x + 1 ， y_{2} = 2 x - 1$ 的“组合函数”，并说明理由；

(2)、设函数 $y_{1} = x - p - 2$ 与 $y_{2} = - x + 3 p$ 的图象相交于点P.
①若 $m + n > 1$ ，点P在函数 $y_{1} 、 y_{2}$ 的“组合函数”图象的上方，求p的取值范围；

②若p≠1，函数 $y_{1} 、 y_{2}$ 的“组合函数”图象经过点P.是否存在大小确定的m值，对于不等于1的任意实数p，都有“组合函数”图象与x轴交点Q的位置不变?若存在，请求出m的值及此时点Q的坐标；若不存在，请说明理由.

查看试题解析
25. 《几何原本》是古希腊数学家欧几里得的一部不朽著作，是数学发展史的一个里程碑.在该书的第2幕“几何与代数”部分，记载了很多利用几何图形来论证的代数结论，利用几何给人以强烈印象将抽象的逻辑规律体现在具体的图形之中.

(1)、我们在学习许多代数公式时，可以用几何图形来推理，观察下列图形，找出可以推出的代数公式，（下面各图形均满足推导各公式的条件，只需填写对应公式的序号）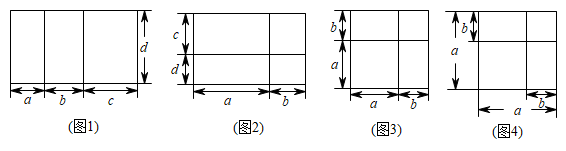

公式①： $(a + b + c) d = a d + b d + c d$

公式②： $(a + b) (c + d) = a c + a d + b c + b d$

公式③： ${(a - b)}^{2} = a^{2} - 2 a b + b^{2}$

公式④： ${(a + b)}^{2} = a^{2} + 2 a b + b^{2}$

图1对应公式，图2对应公式，图3对应公式，图4对应公式；

(2)、《几何原本》中记载了一种利用几何图形证明平方差公式 $(a + b) (a - b) = a^{2} - b^{2}$ 的方法，如图5，请写出证明过程；（已知图中各四边形均为矩形）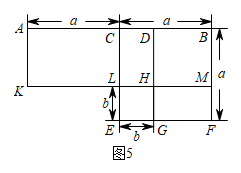

(3)、如图6，在等腰直角三角形ABC中， $∠ B A C = 90 °$ ， D为BC的中点，E为边AC上任意一点（不与端点重合），过点E作 $E G ⊥ B C$ 于点G，作 $E H ⊥ A D$ F点H过点B作BF//AC交EG的延长线于点F.记△BFG与△CEG的面积之和为 $S_{1}$ ， △ABD与△AEH的面积之和为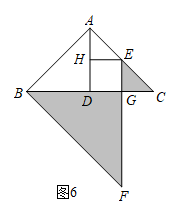 $S_{2}$ .

①若E为边AC的中点，则 $\frac{S_{1}}{S_{2}}$ 的值为 ▲ ；

②若E不为边AC的中点时，试问①中的结论是否仍成立？若成立，写出证明过程；若不成立，请说明理由.

查看试题解析