2023年中考数学精选真题实战测试1 实数A

试卷更新日期：2023-01-02 类型：二轮复习

进入出卷网下载

一、单选题（每题3分，共30分）

1. 实数a、b在数轴.上的对应点位置如图所示，下列结论中正确的是（）

A、 $b > - 2$ B、 $| b | > a$ C、 $a + b > 0$ D、 $a - b < 0$

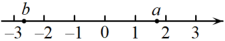查看试题解析
2. 2022年十三届全国人大五次会议审议通过的政府工作报告中提出，今年城镇新增就业目标为11000000人以上.数据11000000用科学记数法表示应为（）

A、 $0.11 \times 1 0^{8}$ B、 $1.1 \times 1 0^{7}$ C、 $11 \times 1 0^{6}$ D、 $1.1 \times 1 0^{6}$

查看试题解析
3. -2的相反数是（）

A、 $- \frac{1}{2}$ B、-2 C、 $\frac{1}{2}$ D、2

查看试题解析
4. 计算结果等于2的是（）

A、 $| - 2 |$ B、 $- | 2 |$ C、 $2^{- 1}$ D、 ${(- 2)}^{0}$

查看试题解析
5. 下列各数是负数的是（）

A、 $(- 1)^{2}$ B、 $| - 3 |$ C、 $- (- 5)$ D、 $\sqrt[3]{- 8}$

查看试题解析
6. 下列运算正确的是（）

A、 $- 2 - 2 = 0$ B、 $\sqrt{8} - \sqrt{2} = \sqrt{6}$ C、 $x^{3} + x^{3} = 2 x^{6}$ D、 $(- x^{3})^{2} = x^{6}$

查看试题解析
7. 已知实数 $a$ ， $b$ 在数轴上的位置如图所示，则 $\frac{a}{| a |} + \frac{b}{| b |}$ 的值是（）

A、-2 B、-1 C、0 D、2

查看试题解析
8. 若气温零上 $2 ℃$ 记作 $+ 2 ℃$ ，则气温零下 $3 ℃$ 记作（）

A、 $- 3 ℃$ B、 $- 1 ℃$ C、 $+ 1 ℃$ D、 $+ 5 ℃$

查看试题解析
9. 如图，数轴上的点A和点B分别在原点的左侧和右侧，点A、B对应的实数分别是a、b，下列结论一定成立的是（）

A、 $a + b < 0$ B、 $b - a < 0$ C、 $2 a > 2 b$ D、 $a + 2 < b + 2$

查看试题解析
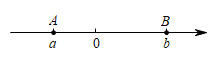10. 如图，M、N、P、Q是数轴上的点，那么 $\sqrt{3}$ 在数轴上对应的点可能是（）

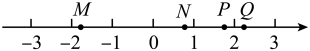A、点A B、点N C、点P D、点Q

查看试题解析

二、填空题（每空3分，共18分）

11. 已知 $a$ ， $b$ 都是实数，若 $| a + 1 | + {(b - 2022)}^{2} = 0$ ，则 $a^{b} =$ ．

查看试题解析
12. “五月天山雪，无花只有寒”，反映出地形对气温的影响．大致海拔每升高100米，气温约下降 $0.6 ° C$ ．有一座海拔为2350米的山，在这座山上海拔为350米的地方测得气温是 $6 ° C$ ，则此时山顶的气温约为 $° C$ ．

查看试题解析
13. 小明和同学们玩扑克牌游戏．游戏规则是：从一副扑克牌（去掉“大王”“小王”）中任意抽取四张，根据牌面上的数字进行混合运算（每张牌上的数字只能用一次），使得运算结果等于24．小明抽到的牌如图所示，请帮小明列出一个结果等于24的算式．

查看试题解析
14. 已知 $a = 2 m^{2} - m n ， b = m n - 2 n^{2} ， c = m^{2} - n^{2} (m \neq n)$ 用“＜”表示 $a 、 b 、 c$ 的大小关系为.

查看试题解析
15. 若 $x = - 3$ ，则 $| x |$ 的值为.

查看试题解析
16. 当今大数据时代，“二维码”具有存储量大.保密性强、追踪性高等特点，它己被广泛应用于我们的日常生活中，尤其在全球“新冠”疫情防控期间，区区“二维码”已经展现出无穷威力.看似“码码相同”，实则“码码不同”.通常，一个“二维码”由1000个大大小小的黑白小方格组成，其中小方格专门用做纠错码和其他用途的编码，这相当于1000个方格只有200个方格作为数据码.根据相关数学知识，这200个方格可以生成 $2^{200}$ 个不同的数据二维码，现有四名网友对 $2^{200}$ 的理解如下：
YYDS（永远的神）： $2^{200}$ 就是200个2相乘，它是一个非常非常大的数；

DDDD（懂的都懂）： $2^{200}$ 等于 $20 0^{2}$ ；

JXND（觉醒年代）： $2^{200}$ 的个位数字是6；

QGYW（强国有我）：我知道 $2^{10} = 1024 ， 1 0^{3} = 1000$ ，所以我估计 $2^{200}$ 比 $1 0^{60}$ 大.

其中对 $2^{200}$ 的理解错误的网友是（填写网名字母代号）.

查看试题解析

三、解答题（共8题，共72分）

17. 计算： ${(- 2)}^{3} + \sqrt{12} + {(\frac{1}{3})}^{- 1}$ ．

查看试题解析
18. 计算： $3 \times (- 1) + 2^{2} + | - 4 |$ ．

查看试题解析
19. 计算： $| - 2 \sqrt{2} | - 3^{- 1} - \sqrt{4} \times \sqrt{2} + (π - 5)^{0}$ .

查看试题解析
20. 计算：（﹣2022）⁰+6×（﹣ $\frac{1}{2}$ ）+ $\sqrt{8}$ ÷ $\sqrt{2}$ ．

查看试题解析
21. 在“-”“×”两个符号中选一个自己想要的符号，填入 $2^{2} + 2 \times (1 □ \frac{1}{2})$ 中的□，并计算.

查看试题解析
22.

(1)、a，b两个实数在数轴上的对应点如图所示.
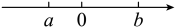
用“<”或“>”填空：ab，ab0；

(2)、在初中阶段我们已经学习了一元二次方程的三种解法，他们分别是配方法、公式法和因式分解法，请从下列一元二次方程中任选两个，并解这两个方程.
①x²+2x−1=0；②x²−3x=0；③x²−4x=4；④x²−4=0.

查看试题解析
23. 第十四届国际数学教育大会（ICME-14）会徽的主题图案有着丰富的数学元素，展现了我国古代数学的文化魅力，其右下方的“卦”是用我国古代的计数符号写出的八进制数3745.八进制是以8作为进位基数的数字系统，有0~7共8个基本数字.八进制数3745换算成十进制数是 $3 \times 8^{3} + 7 \times 8^{2} + 4 \times 8^{1} + 5 \times 8^{0} = 2021$ ，表示ICME-14的举办年份.

(1)、八进制数3746换算成十进制数是；

(2)、小华设计了一个 $n$ 进制数143，换算成十进制数是120，求 $n$ 的值.

查看试题解析
24. 对于任意一个四位数m，若千位上的数字与个位上的数字之和是百位上的数字与十位上的数字之和的2倍，则称这个四位数m为“共生数”例如： $m = 3507$ ，因为 $3 + 7 = 2 \times (5 + 0)$ ，所以3507是“共生数”： $m = 4135$ ，因为 $4 + 5 \neq 2 \times (1 + 3)$ ，所以4135不是“共生数”；

(1)、判断5313，6437是否为“共生数”？并说明理由；

(2)、对于“共生数”n，当十位上的数字是千位上的数字的2倍，百位上的数字与个位上的数字之和能被9整除时，记 $F (n) = \frac{n}{3}$ .求满足 $F (n)$ 各数位上的数字之和是偶数的所有n.

查看试题解析