第二十八章 锐角三角函数 章末测试 人教版九年级下册同步练习
试卷更新日期:2023-01-01 类型:单元试卷
一、单选题
-
1. 已知在Rt△ABC中,∠C=90°,AB=7,BC=5,则sinA=( )A、 B、 C、 D、2. 如图,河坝横断面迎水坡的坡比为: , 坝高m,则的长度为( )
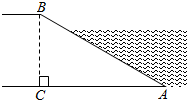 A、6m B、m C、9m D、m3. 已知在中, , , 则的度数是( )A、 B、 C、 D、4. 如图,的顶点在格点(网格线的交点)上,则的值为( )
A、6m B、m C、9m D、m3. 已知在中, , , 则的度数是( )A、 B、 C、 D、4. 如图,的顶点在格点(网格线的交点)上,则的值为( ) A、 B、 C、 D、15. 已知△ABC 中, ∠C=90°,tanA= ,D 是 AC 上一点, ∠CBD=∠A, 则 cos∠CDB的值为( )
A、 B、 C、 D、15. 已知△ABC 中, ∠C=90°,tanA= ,D 是 AC 上一点, ∠CBD=∠A, 则 cos∠CDB的值为( ) A、 B、 C、 D、26. 如图①,在钝角三角形ABC中,AB=AC,D为边AB上一动点(B点除外),以CD为一边作正方形CDEF,连结BE,设BD= , SΔBDE=.若关于的函数图象如图②所示,则sin∠ABC的值为( )
A、 B、 C、 D、26. 如图①,在钝角三角形ABC中,AB=AC,D为边AB上一动点(B点除外),以CD为一边作正方形CDEF,连结BE,设BD= , SΔBDE=.若关于的函数图象如图②所示,则sin∠ABC的值为( )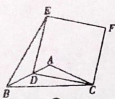
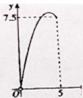
① ②
A、 B、 C、 D、7. 如图,在边长为3的正方形中,点是边上的点,且 , 过点作的垂线交正方形外角的平分线于点 , 交边于点 , 连接交边于点 , 则的长为( )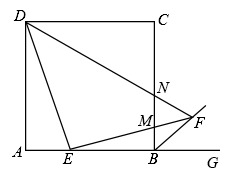 A、 B、 C、 D、1
A、 B、 C、 D、1二、填空题
-
8. 在中,若 , 则9. 在半径为1的圆中,长度等于的弦所对的圆周角是度10. 如图,将一个Rt△ABC形状的楔子从木桩的底点P沿水平方向打入木桩底下,使木桩向上移动.已知楔子斜面的倾斜角为15°,若楔子沿水平方向前进6cm(如箭头所示),则木桩上升了 .(结果可含有三角函数)
 11. 如图1是吊车的实物图,图2是吊车工作示意图,车顶BM与车身CN平行于地面,已知BM到地面的距离为2米,AD=4.8米,∠MBC=3∠BCN.吊车作业时是通过液压杆CD的伸缩使起重臂AB绕点B转动的,从而使得起重臂升降作业.在某次起重作业中,学习兴趣小组经过测量发现:液压杆CD为2米时,∠DCN=120°,∠MBD=150°,则∠CBD=度,此时点A到地面的距离为 米.
11. 如图1是吊车的实物图,图2是吊车工作示意图,车顶BM与车身CN平行于地面,已知BM到地面的距离为2米,AD=4.8米,∠MBC=3∠BCN.吊车作业时是通过液压杆CD的伸缩使起重臂AB绕点B转动的,从而使得起重臂升降作业.在某次起重作业中,学习兴趣小组经过测量发现:液压杆CD为2米时,∠DCN=120°,∠MBD=150°,则∠CBD=度,此时点A到地面的距离为 米. 12. 如图,图中提供了一种求的方法,作 , 使 , , 再延长到点 , 使 , 联结 , 即可得 , 如果设 , 则可得 , 那么 , 运用以上方法,可求得的值是 .
12. 如图,图中提供了一种求的方法,作 , 使 , , 再延长到点 , 使 , 联结 , 即可得 , 如果设 , 则可得 , 那么 , 运用以上方法,可求得的值是 .
三、解答题
-
13. 如图,在中,于点D, , , , 求的长.
 14. 为加强疫情防控工作,某学校决定安装红外线体温检测仪,该设备通过探测人体红外辐射能量对进入测温区域的人员进行快速测温,无需人员停留和接触,安装说明书的部分内容如下表:
14. 为加强疫情防控工作,某学校决定安装红外线体温检测仪,该设备通过探测人体红外辐射能量对进入测温区域的人员进行快速测温,无需人员停留和接触,安装说明书的部分内容如下表:名称
红外线体温检测仪
安装示意图

技术参数
最大探测角:
安装要求
本设备需要安装在垂直于水平地面的支架上,且
问题解决:学校要求测温区域的宽度为4m,师生身高设定为 . 当师生从A走到B时,即可测出人体温度.请你帮助学校确定该设备的安装高度 . (结果精确到m;参考数据 , )
四、综合题
-
15. 如图,在矩形中, , 对角线、交于点O,点M为对角线上一点,连接 , 在内部做射线与线段交于点N(不与点A、点O重合)、与线段交于点P,且 .
 (1)、当 , 求的正切值;(2)、射线交射线与点Q,若 , 求的长;(3)、设线段 , , 写出y关于x的函数关系式,并写出取值范围.
(1)、当 , 求的正切值;(2)、射线交射线与点Q,若 , 求的长;(3)、设线段 , , 写出y关于x的函数关系式,并写出取值范围.