浙教版备考2023年中考数学一轮复习85.数据分析

试卷更新日期：2023-01-01 类型：一轮复习

进入出卷网下载

一、单选题（每题3分，共30分）

1. 某公司对25名营销人员4月份销售某种商品的情况统计如下：
销售量（件）
60
50
40
35
30
20
人数
1
4
4
6
7
3
则这25名营销人员销售量的众数是（）

A、50 B、40 C、35 D、30

查看试题解析
2. 一组数据-2，0，3，1，-1的极差是（）

A、2 B、3 C、4 D、5

查看试题解析
3. 射击比赛中，某队员的10次射击成绩如图所示，则下列结论错误的是（）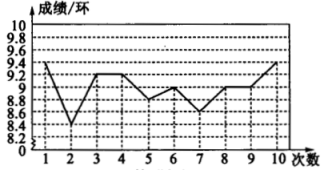

A、平均数是9环 B、中位数是9环 C、众数是9环 D、方差是0.8

查看试题解析
4. 为深入落实“立德树人”的根本任务，坚持德、智、体、美、劳全面发展，某学校积极推进学生综合素质评价改革，某同学在本学期德智体美劳的评价得分如图所示，则该同学五项评价得分的众数，中位数，平均数分别为（）

A、8，8，8 B、7，7，7.8 C、8，8，8.6 D、8，8，8.4

查看试题解析
5. 一组数据：3，4，4，6，若添加一个数据6，则不发生变化的统计量是（）

A、平均数 B、中位数 C、众数 D、方差

查看试题解析
6. 我市某校开展共创文明班，一起向未来的古诗文朗诵比赛活动，有10位同学参加了初赛，按初赛成绩由高到低取前5位进入决赛．如果小王同学知道了自己的成绩后，要判断能否进入决赛，他需要知道这10位同学成绩的（）

A、平均数 B、众数 C、中位数 D、方差

查看试题解析
7. 甲、乙、丙、丁四人进行射击测试，每人10次射击的平均成绩恰好都是9.2环，方差分别是s_甲²＝0.12，s_乙²＝0.59，s_丙²＝0.33，s_丁²＝0.46，在本次射击测试中，这四个人成绩最稳定的是（）

A、甲 B、乙 C、丙 D、丁

查看试题解析
8. 希望中学规定学生的学期体育成绩满分为100，其中体育课外活动占20%，期中考试成绩占30%，期末考试成绩占50%.若小强的三项成绩（百分制）依次是95，90，91.则小强这学期的体育成绩是（）

A、92 B、91.5 C、91 D、90

查看试题解析
9. 第1组数据为：0、0、0、1、1、1，第2组数据为： $\overset{m 个 0}{\overset{︷}{0 ， 0 ， \dots ， 0}}$ 、 $\overset{n 个 1}{\overset{︷}{1 ， 1 ， \dots ， 1}}$ ，其中 $m$ 、 $n$ 是正整数．下列结论：①当 $m = n$ 时，两组数据的平均数相等；②当 $m > n$ 时，第1组数据的平均数小于第2组数据的平均数；③当 $m < n$ 时，第1组数据的中位数小于第2组数据的中位数；④当 $m = n$ 时，第2组数据的方差小于第1组数据的方差．其中正确的是（）

A、①② B、①③ C、①④ D、③④

查看试题解析
10. 家务劳动是劳动教育的一个重要方面，教育部基础教育司发布通知要求家长引导孩子力所能及地做一些家务劳动．某校为了解七年级学生平均每周在家的劳动时间，随机抽取了部分七年级学生进行调查，根据调查结果，绘制了如下频数分布表：
组别
一
二
三
四
劳动时间x/h
$0 \leq x < 1$
$1 \leq x < 2$
$2 \leq x < 3$
$x \geq 3$
频数
10
20
12
8
根据表中的信息，下列说法正确的是（）

A、本次调查的样本容量是50人 B、本次调查七年级学生平均每周在家劳动时间的中位数落在二组 C、本次调查七年级学生平均每周在家劳动时间的众数落在四组 D、若七年级共有500名学生，估计平均每周在家劳动时间在四组的学生大约有100人

查看试题解析

二、填空题（每题4分，共24分）

11. 某书店与一所中学建立帮扶关系，连续6个月向该中学赠送书籍的数量（单位：本）分别为：200，300，400，200，500，550，则这组数据的中位数是本．

查看试题解析
12. 一组2，2x，y，12中，唯一的众数是12，平均数是10，这数据的中位数是．

查看试题解析
13. 学校运动会上，共有15名同学参加了男子100米预赛，参赛选手要想知道自己是否能进入前8名，从而取得决赛资格，只需要了解自己的成绩以及全部成绩的．

查看试题解析
14. 已知一组数据的方差为4，这组数据的标准差是.

查看试题解析
15. 为落实立德树人，发展素质教育，加强美育，需要招聘两位艺术老师，从学历、笔试、上课和现场答辩四个项目进行测试，以最终得分择优录取，甲、乙、丙三位应聘者的测试成绩（10分制）如表所示，如果四项得分按照“1：1：1：1”比例确定每人的最终得分，丙得分最高，甲与乙得分相同，分不出谁将被淘汰；鉴于教师行业应在“上课“项目上权重大一些（其他项目比例相同），为此设计了新的计分比例，你认为三位应聘者中（填：甲、乙或丙）将被淘汰.
成绩
应聘者

甲

乙

丙
学历
9
8
9
笔试
8
7
9
上课
7
8
8
现场答辩
8
9
8

查看试题解析
16. 下表记录了甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数与方差：要从中选择一名发挥稳定的运动员去参加比赛，应该选择．

甲
乙
丙
丁
平均数（cm）
183
183
183
183
方差
5.7
3.5
6.7
8.6

查看试题解析

三、解答题（共8题，共66分）

17. 如图，下列装在相同的透明密封盒内的古钱币，其密封盒上分别标有古钱币的尺寸及质量，例如：钱币“文星高照”密封盒上所标“ $45.4 * 2.8 m m ， 24.4 g$ ”是指该枚古钱币的直径为 $45.4 m m$ ，厚度为 $2.8 m m$ ，质量为 $24.4 g$ ．已知这些古钱币的材质相同．
根据图中信息，解决下列问题．

(1)、这5枚古钱币，所标直径的平均数是 $m m$ ，所标厚度的众数是 $m m$ ，所标质量的中位数是 g；

(2)、由于古钱币无法从密封盒内取出，为判断密封盒上所标古钱币的质量是否有错，桐桐用电子秤测得每枚古钱币与其密封盒的总质量如下：
名称
文星高照
状元及第
鹿鹤同春
顺风大吉
连中三元
总质量/g
58.7
58.1
55.2
54.3
55.8
请你应用所学的统计知识，判断哪枚古钱币所标的质量与实际质量差异较大，并计算该枚古钱币的实际质量约为多少克．

查看试题解析
18. 合理的膳食可以保证青少年体格和智力的正常发育．综合实践小组为了解某校学生膳食营养状况，从该校1380名学生中调查了100名学生的膳食情况，调查数据整理如下：
中国营养学会推荐的三大营养素供能比参考值
蛋白质
10%~15%
脂肪
20%~30%
碳水化合物
50%~65%
注：供能比为某物质提供的能量占人体所需总能量的百分比．

(1)、本次调查采用的调查方法；（填“普查”或“抽样调查”）

(2)、通过对调查数据的计算，样本中的蛋白质平均供能比约为14.6%，请计算样本中的脂肪平均供能比和碳水化合物平均供能比；

(3)、结合以上的调查和计算，对照下表中的参考值，请你针对该校学生膳食状况存在的问题提一条建议．

查看试题解析
19. 2022年5月，W市从甲、乙两校各抽取10名学生参加全市语文素养水平监测．

(1)、【学科测试】每名学生从3套不同的试卷中随机抽取1套作答，小亮、小莹都参加测试，请用树状图或列表法求小亮、小莹作答相同试卷的概率．
样本学生语文测试成绩（满分100分）如下表：

样本学生成绩
平均数
方差
中位数
众数
甲校
50
66
66
66
78
80
81
82
83
94
74.6
141.04
a
66
乙校
64
65
69
74
76
76
76
81
82
83
74.6
40.84
76
b
表中 $a =$ ▲ ； $b =$ ▲ ．
请从平均数、方差、中位数、众数中选择合适的统计量，评判甲、乙两校样本学生的语文测试成绩．

(2)、【问卷调查】对样本学生每年阅读课外书的数量进行问卷调查，根据调查结果把样本学生分为3组，制成频数直方图，如图所示．
A组： $0 < x \leq 20$ ；B组： $20 < x \leq 40$ ；C组： $40 < x \leq 60$ ．
请分别估算两校样本学生阅读课外书的平均数量（取各组上限与下限的中间值近似表示该组的平均数）．

(3)、【监测反思】
①请用【学科测试】和【问卷调查】中的数据，解释语文测试成绩与课外阅读量的相关性；
②若甲、乙两校学生都超过2000人，按照W市的抽样方法，用样本学生数据估计甲、乙两校总体语文素养水平可行吗？为什么？

查看试题解析

20. 综合与实践

【问题情境】数学活动课上，老师带领同学们开展“利用树叶的特征对树木进行分类”的实践活动，

【实践发现】同学们随机收集芒果树、荔枝树的树叶各10片，通过测量得到这些树叶的长y（单位：cm），宽x（单位：cm）的数据后，分别计算长宽比，整理数据如下：

	1	2	3	4	5	6	7	8	9	10
芒果树叶的长宽比	3.8	3.7	3.5	3.4	3.8	4.0	3.6	4.0	3.6	4.0
荔枝树叶的长宽比	2.0	2.0	2.0	2.4	1.8	1.9	1.8	2.0	1.3	1.9

【实践探究】分析数据如下：

	平均数	中位数	众数	方差
芒果树叶的长宽比	3.74	m	4.0	0.0424
荔枝树叶的长宽比	1.91	1.95	n	0.0669

【问题解决】

(1)、上述表格中，

m =

，

n =

；

(2)、①A同学说：“从树叶的长宽比的方差来看，我认为芒果树叶的形状差别大.”

②B同学说：“从树叶的长宽比的平均数、中位数和众数来看，我发现荔枝树叶的长约为宽的两倍.”

上面两位同学的说法中，合理的是（填序号）

(3)、现有一片长

11cm

，宽

5 .6cm

的树叶，请判断这片树叶更可能来自于芒果、荔枝中的哪种树?并给出你的理由.

查看试题解析

21. 为庆祝中国共产主义青年团成立100周年，学校团委在八、九年级各抽取50名团员开展团知识竞赛，为便于统计成绩，制定了取整数的计分方式，满分10分．竞赛成绩如图所示：

众数
中位数
方差
八年级竞赛成绩
7
8
1.88
九年级竞赛成绩
a
8
b

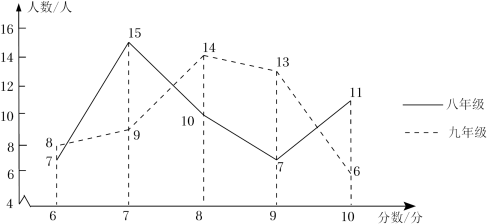(1)、你能用成绩的平均数判断哪个年级的成绩比较好吗？通过计算说明；

(2)、请根据图表中的信息，回答下列问题．
①表中的 $a =$ ▲ ， $b =$ ▲ ；
②现要给成绩突出的年级颁奖，如果分别从众数和方差两个角度来分析，你认为应该给哪个年级颁奖？

(3)、若规定成绩10分获一等奖，9分获二等奖，8分获三等奖，则哪个年级的获奖率高？

查看试题解析
22. 某校举办“歌唱祖国”演唱比赛，十位评委对每位同学的演唱进行现场打分，对参加比赛的甲、乙、丙三位同学得分的数据进行整理、描述和分析，下面给出了部分信息．
a．甲、乙两位同学得分的折线图：
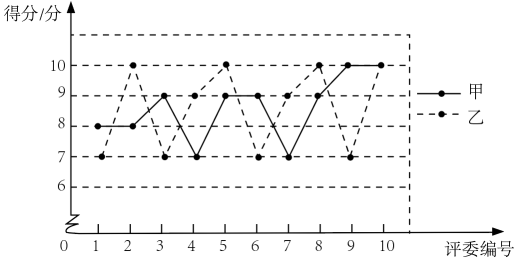
b．丙同学得分：
10，10，10，9，9，8，3，9，8，10
c．甲、乙、丙三位同学得分的平均数：
同学
甲
乙
丙
平均数
8.6
8.6
m
根据以上信息，回答下列问题：

(1)、求表中m的值；

(2)、在参加比赛的同学中，如果某同学得分的10个数据的方差越小，则认为评委对该同学演唱的评价越一致．据此推断：甲、乙两位同学中，评委对的评价更一致（填“甲”或“乙”）；

(3)、如果每位同学的最后得分为去掉十位评委打分中的一个最高分和一个最低分后的平均分，最后得分越高，则认为该同学表现越优秀．据此推断：在甲、乙、丙三位同学中，表现最优秀的是（填“甲”“乙”或“丙”）。

查看试题解析

23. 2022年3月23日下午，“天宫课堂”第二课在中国空间站开讲，神舟十三号乘组航天员翟志刚、王亚平、叶光富相互配合进行授课，这是中国空间站的第二次太空授课，被许多中小学生称为“最牛网课”.某中学为了解学生对“航空航天知识”的掌握情况，随机抽取50名学生进行测试，并对成绩（百分制）进行整理，信息如下：

a.成绩频数分布表：

成绩x（分）	$50 \leq x < 60$	$60 \leq x < 70$	$70 \leq x < 80$	$80 \leq x < 90$	$90 \leq x \leq 100$
频数	7	9	12	16	6

b.成绩在 $70 \leq x < 80$ 这一组的是（单位：分）：

70 71 72 72 74 77 78 78 78 79 79 79

根据以上信息，回答下列问题：

(1)、在这次测试中，成绩的中位数是分，成绩不低于80分的人数占测试人数的百分比为.

(2)、这次测试成绩的平均数是76.4分，甲的测试成绩是77分.乙说：“甲的成绩高于平均数，所以甲的成绩高于一半学生的成绩.”你认为乙的说法正确吗？请说明理由.

(3)、请对该校学生“航空航天知识”的掌握情况作出合理的评价.

查看试题解析

24. 在“双减”政策实施两个月后，某市“双减办”面向本市城区学生，就“‘双减’前后参加校外学科补习班的情况”进行了一次随机问卷调查（以下将“参加校外学科补习班”简称“报班”），根据问卷提交时间的不同，把收集到的数据分两组进行整理，分别得到统计表1和统计图1：

整理描述

表1：“双减”前后报班情况统计表（第一组）

	0	1	2	3	4及以上	合计
“双减”前	102	48	75	51	24	m
“双减”后	255	15	24	n	0	m

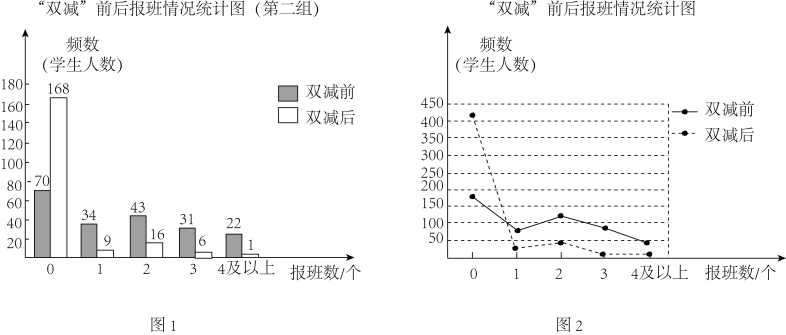(1)、根据表1，m的值为，

\frac{n}{m}

的值为；

(2)、分析处理：请你汇总表1和图1中的数据，求出“双减”后报班数为3的学生人数所占的百分比；

(3)、“双减办”汇总数据后，制作了“双减”前后报班情况的折线统计图（如图2）．请依据以上图表中的信息回答以下问题：

①本次调查中，“双减”前学生报班个数的中位数为， “双减”后学生报班个数的众数为；

②请对该市城区学生“双减”前后报班个数变化情况作出对比分析（用一句话来概括）．

查看试题解析

组别	一	二	三	四
劳动时间x/h	$0 \leq x < 1$	$1 \leq x < 2$	$2 \leq x < 3$	$x \geq 3$
频数	10	20	12	8

成绩应聘者	甲	乙	丙
学历	9	8	9
笔试	8	7	9
上课	7	8	8
现场答辩	8	9	8

名称	文星高照	状元及第	鹿鹤同春	顺风大吉	连中三元
总质量/g	58.7	58.1	55.2	54.3	55.8

中国营养学会推荐的三大营养素供能比参考值
蛋白质	10%~15%
脂肪	20%~30%
碳水化合物	50%~65%

	样本学生成绩										平均数	方差	中位数	众数
甲校	50	66	66	66	78	80	81	82	83	94	74.6	141.04	a	66
乙校	64	65	69	74	76	76	76	81	82	83	74.6	40.84	76	b

销售量（件）	60	50	40	35	30	20
人数	1	4	4	6	7	3

	甲	乙	丙	丁
平均数（cm）	183	183	183	183
方差	5.7	3.5	6.7	8.6

	众数	中位数	方差
八年级竞赛成绩	7	8	1.88
九年级竞赛成绩	a	8	b