浙教版备考2023年中考数学一轮复习83.投影与视图
试卷更新日期:2023-01-01 类型:一轮复习
一、单选题(每题3分,共30分)
-
1. 如图,哪一个是太阳光下形成的影子?( )A、
 B、
B、 C、
C、 D、
D、 2. 由5个大小相同的小正方体搭成的几何体如图所示,它的主视图是( )
2. 由5个大小相同的小正方体搭成的几何体如图所示,它的主视图是( )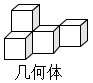 A、
A、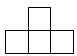 B、
B、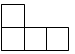 C、
C、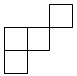 D、
D、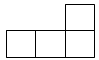 3. 如图,几何体是由六个相同的立方体构成的,则该几何体三视图中面积最大的是( )
3. 如图,几何体是由六个相同的立方体构成的,则该几何体三视图中面积最大的是( )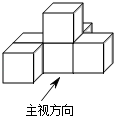 A、主视图 B、左视图 C、俯视图 D、主视图和左视图4. 如图是某一几何体的主视图、左视图、俯视图,该几何体是( )
A、主视图 B、左视图 C、俯视图 D、主视图和左视图4. 如图是某一几何体的主视图、左视图、俯视图,该几何体是( )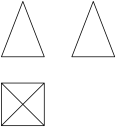 A、四棱柱 B、四棱锥 C、三棱柱 D、三棱锥5. 由一些大小相同的小正方体搭成的几何体的主视图、左视图和俯视图都是如图所示的“田”字形,则搭成该几何体的小正方体的个数最少为( )
A、四棱柱 B、四棱锥 C、三棱柱 D、三棱锥5. 由一些大小相同的小正方体搭成的几何体的主视图、左视图和俯视图都是如图所示的“田”字形,则搭成该几何体的小正方体的个数最少为( )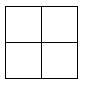 A、4个 B、5个 C、6个 D、7个6. 甲和乙两个几何体都是由大小相同的小立方块搭成,它们的俯视图如图,小正方形中数字表示该位置上的小立方块个数( )
A、4个 B、5个 C、6个 D、7个6. 甲和乙两个几何体都是由大小相同的小立方块搭成,它们的俯视图如图,小正方形中数字表示该位置上的小立方块个数( )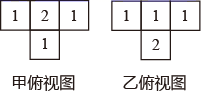 A、甲和乙左视图相同,主视图相同 B、甲和乙左视图不相同,主视图不相同 C、甲和乙左视图相同,主视图不相同 D、甲和乙左视图不相同,主视图相同7. 如图,电灯在横杆的正上方,在灯光下的影长为 , , , , 点到的距离是 , 则点到的距离是( )
A、甲和乙左视图相同,主视图相同 B、甲和乙左视图不相同,主视图不相同 C、甲和乙左视图相同,主视图不相同 D、甲和乙左视图不相同,主视图相同7. 如图,电灯在横杆的正上方,在灯光下的影长为 , , , , 点到的距离是 , 则点到的距离是( ) A、 B、 C、 D、8. 如图,小颖身高为 ,在阳光下影长 ,当她走到距离墙角(点 ) 的 处时,她的部分影子投射到墙上,则投射在墙上的影子 的长度为( )
A、 B、 C、 D、8. 如图,小颖身高为 ,在阳光下影长 ,当她走到距离墙角(点 ) 的 处时,她的部分影子投射到墙上,则投射在墙上的影子 的长度为( ) A、 B、 C、 D、9. 一个直棱柱,主视图是边长为2 的正方形,俯视图是边长为2 的正三角形,则左视图的面积为 ( )A、12 B、12 C、6 D、310. 若干个相同的正方体组成一个几何体,从不同方向看可以得到如图所示的形状,则这个几何体最多可由多少个这样的正方体组成?( )
A、 B、 C、 D、9. 一个直棱柱,主视图是边长为2 的正方形,俯视图是边长为2 的正三角形,则左视图的面积为 ( )A、12 B、12 C、6 D、310. 若干个相同的正方体组成一个几何体,从不同方向看可以得到如图所示的形状,则这个几何体最多可由多少个这样的正方体组成?( )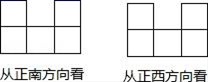 A、12个 B、13个 C、14个 D、18个
A、12个 B、13个 C、14个 D、18个二、填空题(每空3分,共21分)
-
11. 如图所示的4个几何体中,正投影可能是四边形的几何体共有个.
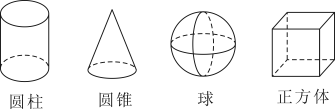 12. 三棱柱的三视图如图所示,在俯视图△EFG中,FG=18cm,EG=14cm,∠EGF=30°,则左视图中AB的长为cm.
12. 三棱柱的三视图如图所示,在俯视图△EFG中,FG=18cm,EG=14cm,∠EGF=30°,则左视图中AB的长为cm. 13. 用小立方体搭一个几何体,分别从它的正面、上面看到的形状如图所示.这样的几何体最少需个小立方体;最多需要个小立方体.
13. 用小立方体搭一个几何体,分别从它的正面、上面看到的形状如图所示.这样的几何体最少需个小立方体;最多需要个小立方体.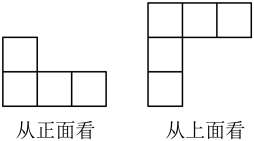 14. 如图,数学兴趣小组下午测得一根长为1m的竹竿影长是0.8m,同一时刻测量树高时发现树的影子有一部分落在教学楼的墙壁上,测得留在墙壁上的影高为1.2m,地面上的影长为2.6m,请你帮算一下,树高是m.
14. 如图,数学兴趣小组下午测得一根长为1m的竹竿影长是0.8m,同一时刻测量树高时发现树的影子有一部分落在教学楼的墙壁上,测得留在墙壁上的影高为1.2m,地面上的影长为2.6m,请你帮算一下,树高是m.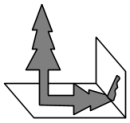 15. 一个由16个完全相同的小立方块搭成的几何体,其最下面一层摆放了9个小立方块,它的主视图和左视图如图所示,那么这个几何体的搭法共有种.
15. 一个由16个完全相同的小立方块搭成的几何体,其最下面一层摆放了9个小立方块,它的主视图和左视图如图所示,那么这个几何体的搭法共有种.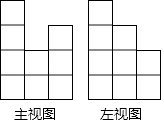
三、解答题(共11题,共66分)
-
16. 请从正面、左面、上面观察, 画出该几何体的三视图




从正面看 从左面看 从上面看
17. 如图,某同学想测量旗杆的高度,他在某一时刻测得1米长的竹竿竖直放置时影长为1.5米,在同一时刻测量旗杆的影长时,因旗杆靠近一楼房,影子不全落在地面上,有一部分落在墙上,他测得落在地面上的影长为21米,落在墙上的影高为6米,求旗杆的高度. 18. 如图,这是一个由小立方块搭成的几何体的俯视图,小正方形中的数字表示该位置的小立方块的个数请你画出它的主视图与左视图.
18. 如图,这是一个由小立方块搭成的几何体的俯视图,小正方形中的数字表示该位置的小立方块的个数请你画出它的主视图与左视图. 19. 为了测量学校旗杆(垂直于水平地面)的高度,班里三个兴趣小组设计了三种不同的测量方案,如下表所示.
19. 为了测量学校旗杆(垂直于水平地面)的高度,班里三个兴趣小组设计了三种不同的测量方案,如下表所示.课题
测量校园旗杆的高度
测量工具
测角仪(测量角度的仪器),卷尺,平面镜等
测量小组
A组
B组
C组
测量方案示意图
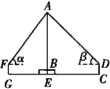
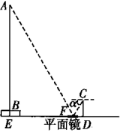
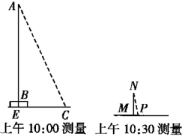
说明
线段AB表示旗杆的高度,线段BE表示旗杆底座高度,点A,B,E共线,线段CD,FG表示测角仪的高度,点A,B,C,D,E,F,G在同一竖直平面内,CG表示两次测角仪摆放位置的距离,测角仪可测得旗杆顶端A的仰角
线段AB表示旗杆的高度,线段BE表示旗杆底座高度,点A,B,E共线,线段CD表示测角仪的高度,DE表示测角仪到旗杆的距离,点F表示平面镜的中心,点E,F,D共线,眼睛在C处,移动平面镜,看向中心F,恰好看到旗杆顶端A,此时用测角仪测得平面镜的俯角,A,B,C,D,E,F六点在同一竖直平面内
线段AB表示旗杆的高度,线段BE表示旗杆底座高度,点A,B,E共线,EC为旗杆与底座某一时刻下的影长,A,B,C,E四点在同一竖直平面内,标杆NM垂直于水平地面,PM为标杆NM在某一时刻的影长
测量数据
为 , 为 , 米,米,米
米,米,米,为
米,米,米,米
(1)、上述A,B,C三个小组中,用哪个小组测量的数据计算出的旗杆高度不是旗杆的真实高度,为什么?(2)、请结合所学知识,利用A组测量的数据计算出旗杆的高度AB.(结果保留两位小数.参考数据: , )20. 如图,公路旁有两个高度相等的路灯AB、CD,小明上午上学时发现路灯AB在太阳光下的影子恰好落在路牌底部E处,他自己的影子恰好落在路灯CD的底部C处;晚自习放学时,站在上午同一个地方,发现在路灯CD的灯光下自己的影子恰好落在E处. (1)、在图中画出小明的位置(用线段FG表示).(2)、若上午上学时,高1米的木棒的影子为2米,小明身高为1.5米,他距离路牌底部E恰好2米,求路灯高.21. 如图,在安装路灯AB的路面CD比种植树木的地面PQ高 , 身高的红英MN站在距离C点15米的路面上.在路灯的照射下,路基CP留在地面上的影长EP为0.4米,
(1)、在图中画出小明的位置(用线段FG表示).(2)、若上午上学时,高1米的木棒的影子为2米,小明身高为1.5米,他距离路牌底部E恰好2米,求路灯高.21. 如图,在安装路灯AB的路面CD比种植树木的地面PQ高 , 身高的红英MN站在距离C点15米的路面上.在路灯的照射下,路基CP留在地面上的影长EP为0.4米, (1)、画出红英MN在地面的影子NF;(2)、若红英留在路面上的影长NF为3m,求路灯AB的高度.22. 如图,用若干个棱长为1cm的小正方体搭成一个几何体.
(1)、画出红英MN在地面的影子NF;(2)、若红英留在路面上的影长NF为3m,求路灯AB的高度.22. 如图,用若干个棱长为1cm的小正方体搭成一个几何体.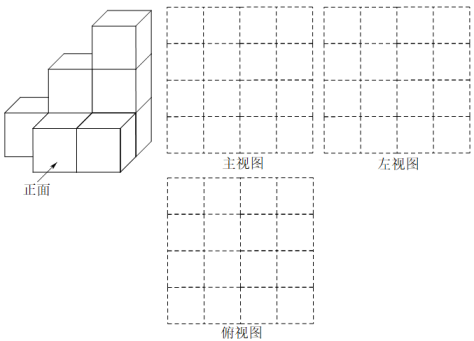 (1)、分别画出这个几何体的三视图;(2)、若将这个几何体外表面涂上一层漆,则其涂漆面积为cm2;(3)、现添加若干个上述小正方体后,若保持左视图和俯视图不变,最多还可以再添加块小正方体.23. 实验学校某班开展数学“综合与实践”测量活动.有两座垂直于水平地面且高度不一的圆柱,两座圆柱后面有一斜坡,且圆柱底部到坡脚水平线 的距离皆为 .王诗嬑观测到高度 矮圆柱的影子落在地面上,其长为 ;而高圆柱的部分影子落在坡上,如图所示.已知落在地面上的影子皆与坡脚水平线 互相垂直,并视太阳光为平行光,测得斜坡坡度 ,在不计圆柱厚度与影子宽度的情况下,请解答下列问题:
(1)、分别画出这个几何体的三视图;(2)、若将这个几何体外表面涂上一层漆,则其涂漆面积为cm2;(3)、现添加若干个上述小正方体后,若保持左视图和俯视图不变,最多还可以再添加块小正方体.23. 实验学校某班开展数学“综合与实践”测量活动.有两座垂直于水平地面且高度不一的圆柱,两座圆柱后面有一斜坡,且圆柱底部到坡脚水平线 的距离皆为 .王诗嬑观测到高度 矮圆柱的影子落在地面上,其长为 ;而高圆柱的部分影子落在坡上,如图所示.已知落在地面上的影子皆与坡脚水平线 互相垂直,并视太阳光为平行光,测得斜坡坡度 ,在不计圆柱厚度与影子宽度的情况下,请解答下列问题: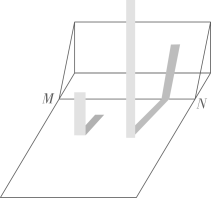
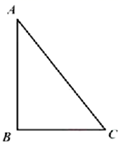 (1)、若王诗嬑的身高为 ,且此刻她的影子完全落在地面上,则影子长为多少 ?(2)、猜想:此刻高圆柱和它的影子与斜坡的某个横截面一定同在一个垂直于地面的平面内.请直接回答这个猜想是否符合题意?(3)、若同一时间量得高圆柱落在坡面上的影子长为 ,则高圆柱的高度为多少 ?24. 用棱长都为5cm的小立方块搭成几何体,从上面看到的几何体的形状图如图所示,其中小正方形中的数字表示在该位置的小立方块的个数.
(1)、若王诗嬑的身高为 ,且此刻她的影子完全落在地面上,则影子长为多少 ?(2)、猜想:此刻高圆柱和它的影子与斜坡的某个横截面一定同在一个垂直于地面的平面内.请直接回答这个猜想是否符合题意?(3)、若同一时间量得高圆柱落在坡面上的影子长为 ,则高圆柱的高度为多少 ?24. 用棱长都为5cm的小立方块搭成几何体,从上面看到的几何体的形状图如图所示,其中小正方形中的数字表示在该位置的小立方块的个数.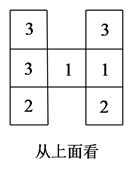 (1)、请你分别画出从正面和从左面看到的这个几何体的形状图;(2)、若在所搭几何体的基础上(不改变原几何体中小立方块的位置),继续添加大小相同的小立方块,以搭成一个大正方体,至少还需要个小立方块;(3)、①图中的几何体的表面积(包括与桌面接触的部分)为 ;
(1)、请你分别画出从正面和从左面看到的这个几何体的形状图;(2)、若在所搭几何体的基础上(不改变原几何体中小立方块的位置),继续添加大小相同的小立方块,以搭成一个大正方体,至少还需要个小立方块;(3)、①图中的几何体的表面积(包括与桌面接触的部分)为 ;②若新搭一个几何体,且满足如下三个条件:图中从上面看到的几何体的形状图不变,小立方块的总数不变,从上面看到的小正方形中的数字可以改变,则新搭几何体的表面积(包括与桌面接触的部分)最小值和最大值分别为 , .
25. 如图,A、B、C分别表示甲、乙、丙三个物体的顶端,甲物体高3米,影长2米,乙物体高2米,影长3米,甲乙两物体相距4米. (1)、请在图中画出光源灯的位置及灯杆,并画出物体丙的影子.(2)、若甲、乙、丙及灯杆都与地面垂直,且在同一直线上,求灯杆的高度.26. 用棱长为 的若干小正方体按如所示的规律在地面上搭建若干个几何体.图中每个几何体自上而下分别叫第一层、第二层, ,第 层( 为正整数)
(1)、请在图中画出光源灯的位置及灯杆,并画出物体丙的影子.(2)、若甲、乙、丙及灯杆都与地面垂直,且在同一直线上,求灯杆的高度.26. 用棱长为 的若干小正方体按如所示的规律在地面上搭建若干个几何体.图中每个几何体自上而下分别叫第一层、第二层, ,第 层( 为正整数)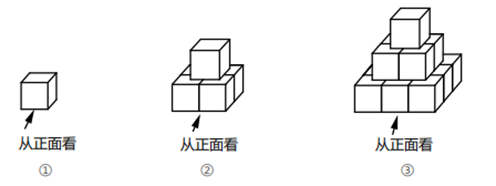 (1)、搭建第④个几何体的小立方体的个数为 .(2)、分别求出第②、③个几何体的所有露出部分(不含底面)的面积.(3)、为了美观,若将几何体的露出部分都涂上油漆(不含底面),已知喷涂 需要油漆0.2克,求喷涂第20个几何体,共需要多少克油漆?
(1)、搭建第④个几何体的小立方体的个数为 .(2)、分别求出第②、③个几何体的所有露出部分(不含底面)的面积.(3)、为了美观,若将几何体的露出部分都涂上油漆(不含底面),已知喷涂 需要油漆0.2克,求喷涂第20个几何体,共需要多少克油漆?