浙教版备考2023年中考数学一轮复习81.锐角三角函数
试卷更新日期:2023-01-01 类型:一轮复习
一、单选题(每题3分,共30分)
-
1. 如图,在网格正方形中,每个小正方形的边长为1,顶点为格点,若的顶点均是格点,则的值是( )
 A、 B、 C、 D、2. 由4个形状相同,大小相等的菱形组成如图所示的网格,菱形的顶点称为格点,点A,B,C都在格点上,∠O=60°,则tan∠ABC=( )
A、 B、 C、 D、2. 由4个形状相同,大小相等的菱形组成如图所示的网格,菱形的顶点称为格点,点A,B,C都在格点上,∠O=60°,则tan∠ABC=( ) A、 B、 C、 D、3. 计算的结果,正确的是( )A、 B、 C、 D、4. 如图所示的衣架可以近似看成一个等腰三角形ABC,其中AB=AC, , BC=44cm,则高AD约为( )(参考数据: , , )
A、 B、 C、 D、3. 计算的结果,正确的是( )A、 B、 C、 D、4. 如图所示的衣架可以近似看成一个等腰三角形ABC,其中AB=AC, , BC=44cm,则高AD约为( )(参考数据: , , )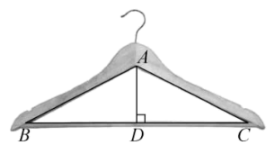 A、9.90cm B、11.22cm C、19.58cm D、22.44cm5. 如图,在平面直角坐标系中,点A,B分别在x轴负半轴和y轴正半轴上,点C在OB上, ,连接AC,过点O作 交AC的延长线于P.若 ,则 的值是( )
A、9.90cm B、11.22cm C、19.58cm D、22.44cm5. 如图,在平面直角坐标系中,点A,B分别在x轴负半轴和y轴正半轴上,点C在OB上, ,连接AC,过点O作 交AC的延长线于P.若 ,则 的值是( ) A、 B、 C、 D、36. 中国古代数学家赵爽在为《周髀算经》作注解时,用4个全等的直角三角形拼成正方形(如图),并用它证明了勾股定理,这个图被称为“弦图”,若“弦图”中小正方形面积与每个直角三角形面积均为1,α为直角三角形中的一个锐角,则tanα=( )
A、 B、 C、 D、36. 中国古代数学家赵爽在为《周髀算经》作注解时,用4个全等的直角三角形拼成正方形(如图),并用它证明了勾股定理,这个图被称为“弦图”,若“弦图”中小正方形面积与每个直角三角形面积均为1,α为直角三角形中的一个锐角,则tanα=( )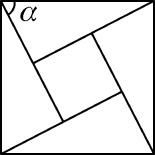 A、2 B、 C、 D、7. 如图,在 中, , , ,若用科学计算器求AC的长,则下列按键顺序正确的是( )
A、2 B、 C、 D、7. 如图,在 中, , , ,若用科学计算器求AC的长,则下列按键顺序正确的是( )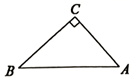 A、 B、 C、 D、8. 如图,在6×6的正方形网格中,每个小正方形的边长都是1,点A,B,C均在网格交点上,⊙O是△ABC的外接圆,则sin∠BAC的值为( )
A、 B、 C、 D、8. 如图,在6×6的正方形网格中,每个小正方形的边长都是1,点A,B,C均在网格交点上,⊙O是△ABC的外接圆,则sin∠BAC的值为( )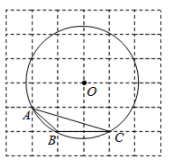 A、 B、 C、 D、9. 将一矩形纸片ABCD沿CE折叠,B点恰好落在AD边上的F处,若 ,则 的值为( )
A、 B、 C、 D、9. 将一矩形纸片ABCD沿CE折叠,B点恰好落在AD边上的F处,若 ,则 的值为( )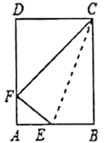 A、 B、 C、 D、10. 已知 ,则 的度数所属范围是( )A、
A、 B、 C、 D、10. 已知 ,则 的度数所属范围是( )A、 B、
C、
D、
B、
C、
D、
二、填空题(每题4分,共24分)
-
11. 如图,在Rt△ABC中,∠C=90°,若sinA= , 则cosB= .
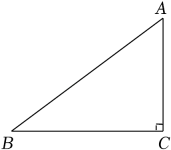 12. 阅读材料:余弦定理是描述三角形中三边长度与一个角余弦值关系的数学定理,运用它可以解决一类已知三角形两边及夹角求第三边或者已知三边求角的问题.余弦定理是这样描述的:在△ABC中,∠A、∠B、∠C所对的边分别为a、b、c,则三角形中任意一边的平方等于另外两边的平方和减去这两边及这两边的夹角的余弦值的乘积的2倍.
12. 阅读材料:余弦定理是描述三角形中三边长度与一个角余弦值关系的数学定理,运用它可以解决一类已知三角形两边及夹角求第三边或者已知三边求角的问题.余弦定理是这样描述的:在△ABC中,∠A、∠B、∠C所对的边分别为a、b、c,则三角形中任意一边的平方等于另外两边的平方和减去这两边及这两边的夹角的余弦值的乘积的2倍.用公式可描述为:a2=b2+c2﹣2bccosA
b2=a2+c2﹣2accosB
c2=a2+b2﹣2abcosC
现已知在△ABC中,AB=3,AC=4,∠A=60°,则BC= .
13. 下列结论中(其中 , 均为锐角),正确的是 . (填序号)① ;② ;③当 时, ;④ .
14. 北京冬奥会开幕式的巨型雪花状主火炬塔的设计,体现了环保低碳理念.如图所示,它的主体形状呈正六边形.若点A,F,B,D,C,E是正六边形的六个顶点,则tan∠ABE= . 15. 数学小组研究如下问题:遵义市某地的纬度约为北纬28°,求北纬28纬线的长度.
15. 数学小组研究如下问题:遵义市某地的纬度约为北纬28°,求北纬28纬线的长度.小组成员查阅相关资料,得到如下信息:
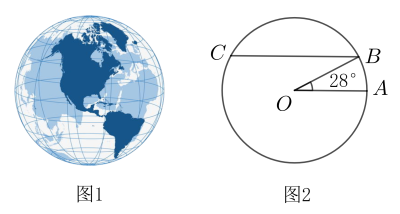
信息一:如图1,在地球仪上,与赤道平行的圆圈叫做纬线;
信息二:如图2,赤道半径约为6400千米,弦 , 以为直径的圆的周长就是北纬28°纬线的长度;(参考数据: , , , )
根据以上信息,北纬28°纬线的长度约为千米.
 16. 如图,直线 与x轴交于点M,与y轴交于点A,过点A作 ,交x轴于点B,以AB为边在AB的右侧作正方形ABCA1 , 延长A1C交x轴于点B1 , 以A1B1为边在A1B1的右侧作正方形A1B1C1A2…按照此规律继续作下去,再将每个正方形分割成四个全等的直角三角形和一个小正方形,每个小正方形的每条边都与其中的一条坐标轴平行,正方形ABCA1 , A1B1C1A2 , …, 中的阴影部分的面积分别为S1 , S2 , …,Sn , 则Sn可表示为.
16. 如图,直线 与x轴交于点M,与y轴交于点A,过点A作 ,交x轴于点B,以AB为边在AB的右侧作正方形ABCA1 , 延长A1C交x轴于点B1 , 以A1B1为边在A1B1的右侧作正方形A1B1C1A2…按照此规律继续作下去,再将每个正方形分割成四个全等的直角三角形和一个小正方形,每个小正方形的每条边都与其中的一条坐标轴平行,正方形ABCA1 , A1B1C1A2 , …, 中的阴影部分的面积分别为S1 , S2 , …,Sn , 则Sn可表示为.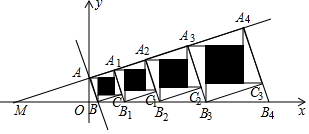
三、计算题(共2题,共12分)
-
17. 计算:18. 用计算器求下列各式的值:(1)、 ;(2)、 ;(3)、 .
四、作图题(共9分)
-
19. 如图,正方形网格中的每一个小正方形的边长都是1,四边形ABCD的四个顶点都在格点上,O为AD边的中点,若把四边形ABCD绕着点O顺时针旋转,试解决下列问题:

( 1 )画出四边形ABCD旋转180°后的图形;
( 2 )求点C旋转过程中所经过的路径长;
( 3 )求sin∠BAD的值.
五、解答题(共5题,共45分)
-
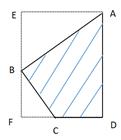
20. 学生到工厂劳动实践,学习机械零件,零件的截面如图所示,已知四边形AEFD为矩形,点B,C分别在EF,DF上,∠ABC为90°,∠BAD=53°,AB=10cm,BC=6cm,求零件的截面面积.
参考数据:sin53°≈0.80,cos53°≈0.60.
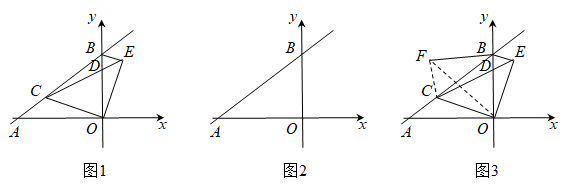
 21. 知识再现:如图1,在Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边分别为a,b,c.
21. 知识再现:如图1,在Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边分别为a,b,c.∵ ,
∴ ,
∴
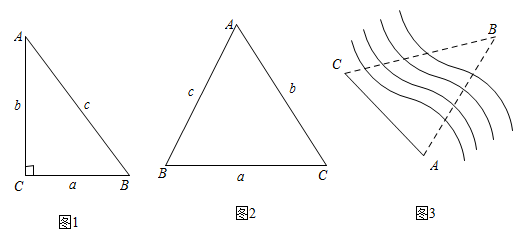 (1)、拓展探究:如图2,在锐角ABC中,∠A,∠B,∠C的对边分别为a,b,c.请探究 , , 之间的关系,并写出探究过程.(2)、解决问题:如图3,为测量点A到河对岸点B的距离,选取与点A在河岸同一侧的点C,测得AC=60m,∠A=75°,∠C=60°.请用拓展探究中的结论,求点A到点B的距离.22. 一个一次函数的截距为1,且经过点A(2,3).(1)、求这个一次函数的解析式;(2)、点A,B在某个反比例函数上,点B横坐标为6,将点B向上平移2个单位得到点C,求cos∠ABC的值.
(1)、拓展探究:如图2,在锐角ABC中,∠A,∠B,∠C的对边分别为a,b,c.请探究 , , 之间的关系,并写出探究过程.(2)、解决问题:如图3,为测量点A到河对岸点B的距离,选取与点A在河岸同一侧的点C,测得AC=60m,∠A=75°,∠C=60°.请用拓展探究中的结论,求点A到点B的距离.22. 一个一次函数的截距为1,且经过点A(2,3).(1)、求这个一次函数的解析式;(2)、点A,B在某个反比例函数上,点B横坐标为6,将点B向上平移2个单位得到点C,求cos∠ABC的值.
-