浙教版备考2023年中考数学一轮复习80.相似三角形的性质与判定
试卷更新日期:2023-01-01 类型:一轮复习
一、单选题(每题3分,共36分)
-
1. 下列各组中两个图形不相似的是( )A、
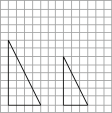 B、
B、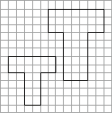 C、
C、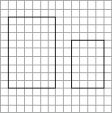 D、
D、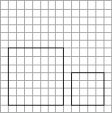 2. 下列各组图形中,一定相似的是( )A、两个正方形 B、两个矩形 C、两个菱形 D、两个平行四边形3. 下列命题中,属于真命题的是( )A、两个菱形一定相似 B、两个等腰直角三角形一定相似 C、两个矩形一定相似 D、两个周长相等的三角形一定相似4. 下列图形中,一定相似的是( )A、一条直线截三角形两边所得的三角形与原三角形 B、有一个内角为80°的两个等腰三角形 C、两个长方形 D、有一个内角为80°的两个菱形5. △ABC的三边长分别为2,3,4,另有一个与它相似的三角形 DEF ,其最长边为12,则 △DEF的周长是( )A、54 B、36 C、27 D、216. 如图,以点O为位似中心,作四边形 的位似图形 ﹐已知 ,若四边形 的面积是2,则四边形 的面积是( )
2. 下列各组图形中,一定相似的是( )A、两个正方形 B、两个矩形 C、两个菱形 D、两个平行四边形3. 下列命题中,属于真命题的是( )A、两个菱形一定相似 B、两个等腰直角三角形一定相似 C、两个矩形一定相似 D、两个周长相等的三角形一定相似4. 下列图形中,一定相似的是( )A、一条直线截三角形两边所得的三角形与原三角形 B、有一个内角为80°的两个等腰三角形 C、两个长方形 D、有一个内角为80°的两个菱形5. △ABC的三边长分别为2,3,4,另有一个与它相似的三角形 DEF ,其最长边为12,则 △DEF的周长是( )A、54 B、36 C、27 D、216. 如图,以点O为位似中心,作四边形 的位似图形 ﹐已知 ,若四边形 的面积是2,则四边形 的面积是( )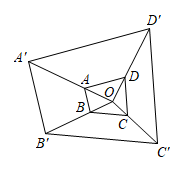 A、4 B、6 C、16 D、187. 如图,在平面直角坐标系中,为的边上一点, , 过作交于点 , 、两点纵坐标分别为1、3,则点的纵坐标为( )
A、4 B、6 C、16 D、187. 如图,在平面直角坐标系中,为的边上一点, , 过作交于点 , 、两点纵坐标分别为1、3,则点的纵坐标为( )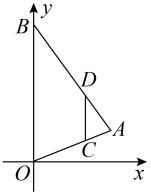 A、4 B、5 C、6 D、78. 已知两个直角三角形的三边长分别为3,4, 和6,8, ,且这两个直角三角形不相似,则 的值为( )A、 或 B、15 C、 D、9. 矩形相邻的两边长分别为25和 , 把它按如图所示的方式分割成五个全等的小矩形,每一个小矩形均与原矩形相似,则的值为( )
A、4 B、5 C、6 D、78. 已知两个直角三角形的三边长分别为3,4, 和6,8, ,且这两个直角三角形不相似,则 的值为( )A、 或 B、15 C、 D、9. 矩形相邻的两边长分别为25和 , 把它按如图所示的方式分割成五个全等的小矩形,每一个小矩形均与原矩形相似,则的值为( )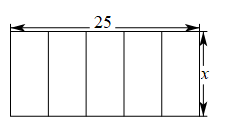 A、5 B、 C、 D、1010. 两相似多边形的面积比是 , 较小多边形的周长为 , 则较大多边形的周长为( )A、 B、 C、 D、11. 西周数学家商高总结了用“矩”(如图1)测量物高的方法:把矩的两边放置成如图2的位置,从矩的一端A(人眼)望点E,使视线通过点C,记人站立的位置为点B,量出BG长,即可算得物高EG.令BG=x(m), EG=y(m),若a=30cm,b=60cm,AB=1.6m,则y关于x的函数表达式为( )
A、5 B、 C、 D、1010. 两相似多边形的面积比是 , 较小多边形的周长为 , 则较大多边形的周长为( )A、 B、 C、 D、11. 西周数学家商高总结了用“矩”(如图1)测量物高的方法:把矩的两边放置成如图2的位置,从矩的一端A(人眼)望点E,使视线通过点C,记人站立的位置为点B,量出BG长,即可算得物高EG.令BG=x(m), EG=y(m),若a=30cm,b=60cm,AB=1.6m,则y关于x的函数表达式为( )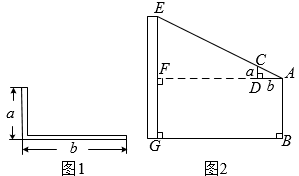 A、 B、 C、 D、12. 由12个有公共顶点O的直角三角形拼成如图所示的图形,∠AOB=∠BOC=∠COD=…=∠LOM=30°.若S△AOB=1,则图中与△AOB位似的三角形的面积为( )
A、 B、 C、 D、12. 由12个有公共顶点O的直角三角形拼成如图所示的图形,∠AOB=∠BOC=∠COD=…=∠LOM=30°.若S△AOB=1,则图中与△AOB位似的三角形的面积为( )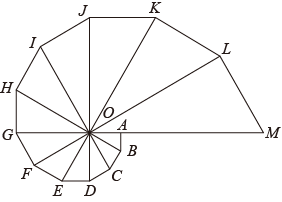 A、()3 B、()7 C、()6 D、()6
A、()3 B、()7 C、()6 D、()6二、填空题(每题4分,共24分)
-
13. 如图,在中,点在边上,点在边上,请添加一个条件 , 使.
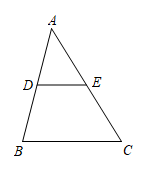 14. 如图, , , 相交于点 , 若 , , 则的长为 .
14. 如图, , , 相交于点 , 若 , , 则的长为 .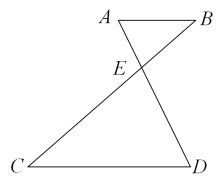 15. 已知与是位似图形,位似比是 , 则与的面积比 .16. 《墨子·天文志》记载:“执规矩,以度天下之方圆.”度方知圆,感悟数学之美.如图,正方形的面积为4,以它的对角线的交点为位似中心,作它的位似图形 , 若 , 则四边形的外接圆的周长为 .
15. 已知与是位似图形,位似比是 , 则与的面积比 .16. 《墨子·天文志》记载:“执规矩,以度天下之方圆.”度方知圆,感悟数学之美.如图,正方形的面积为4,以它的对角线的交点为位似中心,作它的位似图形 , 若 , 则四边形的外接圆的周长为 .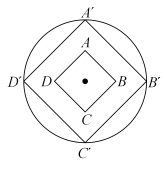 17. 数学兴趣小组通过测量旗杆的影长来求旗杆的高度,他们在某一时刻测得高为2米的标杆影长为1.2米,此时旗杆影长为7.2米,则旗杆的高度为米.
17. 数学兴趣小组通过测量旗杆的影长来求旗杆的高度,他们在某一时刻测得高为2米的标杆影长为1.2米,此时旗杆影长为7.2米,则旗杆的高度为米.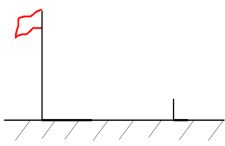 18. 如图,在平面直角坐标系中,与位似,位似中心是坐标原点O.若点 , 点 , 则与周长的比值是 .
18. 如图,在平面直角坐标系中,与位似,位似中心是坐标原点O.若点 , 点 , 则与周长的比值是 .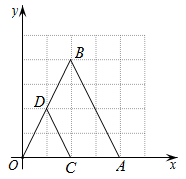
三、解答题(共7题,共60分)
-
19. 如图,在7×4方格纸中,点A,B,C都在格点上,用无刻度直尺作图.
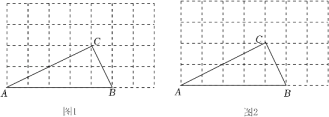 (1)、在图1中的线段AC上找一个点E,使AE=AC;(2)、在图2中作一个格点△CDE,使△CDE与△ABC相似.20. 如图,在中, , E是边AC上一点,且 , 过点A作BE的垂线,交BE的延长线于点D,求证: .
(1)、在图1中的线段AC上找一个点E,使AE=AC;(2)、在图2中作一个格点△CDE,使△CDE与△ABC相似.20. 如图,在中, , E是边AC上一点,且 , 过点A作BE的垂线,交BE的延长线于点D,求证: .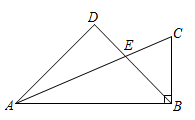 21. 如图,某水渠的横断面是以AB为直径的半圆O , 其中水面截线 .嘉琪在A处测得垂直站立于B处的爸爸头顶C的仰角为14°,点M的俯角为7°.已知爸爸的身高为1.7m .
21. 如图,某水渠的横断面是以AB为直径的半圆O , 其中水面截线 .嘉琪在A处测得垂直站立于B处的爸爸头顶C的仰角为14°,点M的俯角为7°.已知爸爸的身高为1.7m .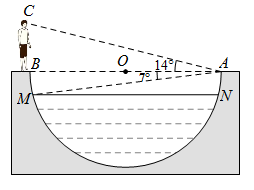 (1)、求∠C的大小及AB的长;(2)、请在图中画出线段DH , 用其长度表示最大水深(不说理由),并求最大水深约为多少米(结果保留小数点后一位).(参考数据: 取4, 取4.1)22. 学习了相似三角形知识后,小丽同学准备用自制的直角三角形纸板测量校园内一颗古树的高度.已知三角形纸板的斜边长为0.5米,较短的直角边长为0.3米.
(1)、求∠C的大小及AB的长;(2)、请在图中画出线段DH , 用其长度表示最大水深(不说理由),并求最大水深约为多少米(结果保留小数点后一位).(参考数据: 取4, 取4.1)22. 学习了相似三角形知识后,小丽同学准备用自制的直角三角形纸板测量校园内一颗古树的高度.已知三角形纸板的斜边长为0.5米,较短的直角边长为0.3米.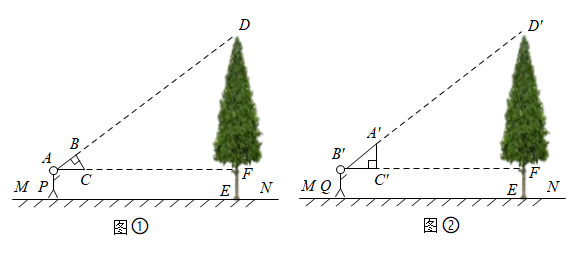 (1)、小丽先调整自己的位置至点 , 将直角三角形纸板的三个顶点位置记为、、(如图①),斜边平行于地面(点、、、在一直线上),且点在边(较长直角边)的延长线上,此时测得边距离地面的高度为1.5米,小丽与古树的距离为16米,求古树的高度;(2)、为了尝试不同的思路,小丽又向前移动自己的位置至点 , 将直角三角形纸板的三个顶点的新位置记为、、(如图②),使直角边(较短直角边)平行于地面(点、、、在一直线上),点在斜边的延长线上,且测得此时边距离地面的高度依然是1.5米,那么小丽向前移动了多少米?23. 如图,一次函数与反比例函数的图象交于点 , 与轴交于点 .
(1)、小丽先调整自己的位置至点 , 将直角三角形纸板的三个顶点位置记为、、(如图①),斜边平行于地面(点、、、在一直线上),且点在边(较长直角边)的延长线上,此时测得边距离地面的高度为1.5米,小丽与古树的距离为16米,求古树的高度;(2)、为了尝试不同的思路,小丽又向前移动自己的位置至点 , 将直角三角形纸板的三个顶点的新位置记为、、(如图②),使直角边(较短直角边)平行于地面(点、、、在一直线上),点在斜边的延长线上,且测得此时边距离地面的高度依然是1.5米,那么小丽向前移动了多少米?23. 如图,一次函数与反比例函数的图象交于点 , 与轴交于点 .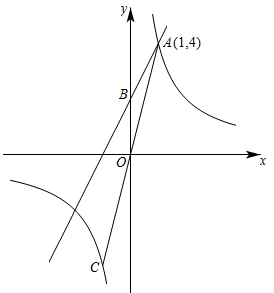 (1)、 , ;(2)、连接并延长 , 与反比例函数的图象交于点 , 点在轴上,若以、、为顶点的三角形与相似,求点的坐标.24. 如图,在菱形ABCD中,AB=5,BD为对角线.点E是边AB延长线上的任意一点,连结DE交BC于点F,BG平分∠CBE交DE于点G.
(1)、 , ;(2)、连接并延长 , 与反比例函数的图象交于点 , 点在轴上,若以、、为顶点的三角形与相似,求点的坐标.24. 如图,在菱形ABCD中,AB=5,BD为对角线.点E是边AB延长线上的任意一点,连结DE交BC于点F,BG平分∠CBE交DE于点G. (1)、求证:.(2)、若 .
(1)、求证:.(2)、若 .①求菱形的面积.
②求的值.
(3)、若 , 当的大小发生变化时(),在AE上找一点T,使GT为定值,说明理由并求出ET的值.25. 综合与探究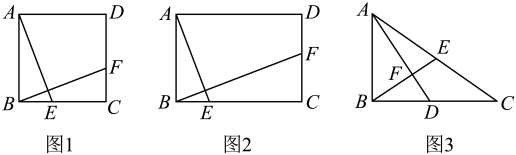 (1)、如图1,在正方形中,点分别在边上,且 , 请直接写出线段与的数量关系 .(2)、【类比探究】
(1)、如图1,在正方形中,点分别在边上,且 , 请直接写出线段与的数量关系 .(2)、【类比探究】如图2,在矩形中, , , 点分别在边上,且 , 请写出线段与的数量关系,并证明你的结论.
(3)、【拓展延伸】如图3,在中, , D为中点,连接 , 过点B作于点F,交于点E,若 , , 求的长.