浙教版备考2023年中考数学一轮复习79.比例与比例线段
试卷更新日期:2023-01-01 类型:一轮复习
一、单选题(每题3分,共30分)
-
1. 下列四条线段中,能成为成比例线段的是( )A、 , , , B、 , , , C、 , , , D、 , , ,2. 如果线段 , 那么a和b的比例中项是( )A、 B、 C、 D、3. 如果 , 那么下列各式不一定成立的是( )A、 B、 C、 D、4. 已知 , 则的值是( )A、 B、 C、 D、5. 在比例尺为1:100000的地图上,甲、乙两地图距是2cm,它的实际长度约为( )A、100km B、2000m C、10km D、20km6. 已知:线段a,b,c,求作线段x,使x= , 以下作法正确的是( )A、
 B、
B、 C、
C、 D、
D、 7. 如图,点D为边上任一点,交于点E,连接相交于点F,则下列等式中不成立的是( )
7. 如图,点D为边上任一点,交于点E,连接相交于点F,则下列等式中不成立的是( ) A、 B、 C、 D、8. 如图,五线谱是由等距离、等长度的五条平行横线组成的,同一条直线上的三个点A,B,C都在横线上:若线段AB=3,则线段BC的长是( )
A、 B、 C、 D、8. 如图,五线谱是由等距离、等长度的五条平行横线组成的,同一条直线上的三个点A,B,C都在横线上:若线段AB=3,则线段BC的长是( ) A、 B、1 C、 D、29. 秦兵马俑的发现被誉为“世界第八大奇迹”,兵马俑的眼睛到下巴的距离与头顶到下巴的距离之比约为 , 下列估算正确的是( )
A、 B、1 C、 D、29. 秦兵马俑的发现被誉为“世界第八大奇迹”,兵马俑的眼睛到下巴的距离与头顶到下巴的距离之比约为 , 下列估算正确的是( ) A、 B、 C、 D、10. 如图,在中, , 分别以点A和点C为圆心,大于的长为半径作弧,两弧相交于M,N两点,作直线 , 直线与相交于点D,连接 , 若 , 则的长是( )
A、 B、 C、 D、10. 如图,在中, , 分别以点A和点C为圆心,大于的长为半径作弧,两弧相交于M,N两点,作直线 , 直线与相交于点D,连接 , 若 , 则的长是( )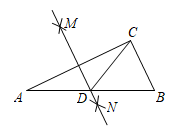 A、6 B、3 C、1.5 D、1
A、6 B、3 C、1.5 D、1二、填空题(每题4分,共24分)
-
11. 四条线段a、b、c、d成比例,满足 , 其中m,m,m,则a=m.12. 如图,已知是内的一点, , , 若的面积为2, , , 则的面积是.
 13. 如图,圆中扇子对应的圆心角()与剩余圆心角的比值为黄金比时,扇子会显得更加美观,若黄金比取0.6,则的度数是 .
13. 如图,圆中扇子对应的圆心角()与剩余圆心角的比值为黄金比时,扇子会显得更加美观,若黄金比取0.6,则的度数是 .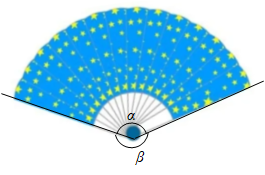 14. 如图,在△ABC中,边AB在x轴上,边AC交y轴于点E.反比例函数的图象恰好经过点C,与边BC交于点D.若AE=CE,CD=2BD, , 则k= .
14. 如图,在△ABC中,边AB在x轴上,边AC交y轴于点E.反比例函数的图象恰好经过点C,与边BC交于点D.若AE=CE,CD=2BD, , 则k= .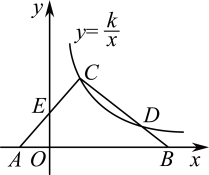 15. 九年级融融陪同父母选购家装木地板,她感觉某品牌木地板拼接图(如实物图)比较美观,通过手绘(如图)、测量、计算发现点是的黄金分割点,即.延长与相交于点 , 则.(精确到0.001)
15. 九年级融融陪同父母选购家装木地板,她感觉某品牌木地板拼接图(如实物图)比较美观,通过手绘(如图)、测量、计算发现点是的黄金分割点,即.延长与相交于点 , 则.(精确到0.001)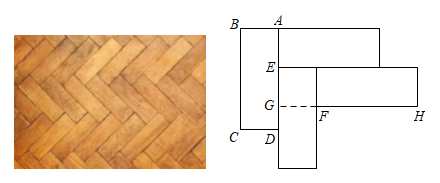 16. 在20世纪70年代,我国著名数学家华罗庚教授将黄金分割法作为一种“优选法”,在全国大规模推广,取得了很大成果.如图,利用黄金分割法,所做将矩形窗框分为上下两部分,其中E为边的黄金分割点,即.已知为2米,则线段的长为米.
16. 在20世纪70年代,我国著名数学家华罗庚教授将黄金分割法作为一种“优选法”,在全国大规模推广,取得了很大成果.如图,利用黄金分割法,所做将矩形窗框分为上下两部分,其中E为边的黄金分割点,即.已知为2米,则线段的长为米.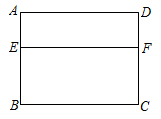
三、作图题(共9分)
-
17. 如图,将线段AB放在边长为1的小正方形网格,点A点B均落在格点上,请用无刻度直尺在图中按要求作出所求的点.
 (1)、如图一,将线段AB三等分(2)、如图二,使AP= ,并保留作图痕迹。(3)、如图三,在△ABC内部找一点P,使得S△PAB:S△PBC:S△PAC=1:2:3
(1)、如图一,将线段AB三等分(2)、如图二,使AP= ,并保留作图痕迹。(3)、如图三,在△ABC内部找一点P,使得S△PAB:S△PBC:S△PAC=1:2:3四、解答题(共7题,共57分)
-
18. 已知实数a、b、c满足 , 且 . 求:的值.19. 如图,直线l1∥l2∥l3 , 直线AC依次交l1 , l2 , l3于A,B,C三点,直线DF依次交l1 , l2 , l3于D,E,F三点,若 ,DE=12,求EF的长.
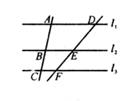 20. 如图
20. 如图 (1)、如图1,在△ABC中, ,CD平分 ,交AB于点D, // ,交BC于点E.
(1)、如图1,在△ABC中, ,CD平分 ,交AB于点D, // ,交BC于点E.①若 , ,求BC的长;
②试探究 是否为定值.如果是,请求出这个定值;如果不是,请说明理由.
(2)、如图2, 和 是△ABC的2个外角, ,CD平分 ,交AB的延长线于点D, // ,交CB的延长线于点E.记△ACD的面积为 ,△CDE的面积为 ,△BDE的面积为 .若 ,求 的值.21.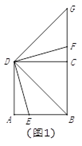
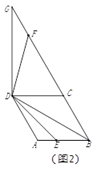
 (1)、如图1, 是正方形 边 上的一点,连接 ,将 绕着点 逆时针旋转90°,旋转后角的两边分别与射线 交于点 和点 .
(1)、如图1, 是正方形 边 上的一点,连接 ,将 绕着点 逆时针旋转90°,旋转后角的两边分别与射线 交于点 和点 .①线段 和 的数量关系是 ▲ ;
②写出线段 和 之间的数量关系.
(2)、当四边形 为菱形, ,点 是菱形 边 所在直线上的一点,连接 ,将 绕着点 逆时针旋转120°,旋转后角的两边分别与射线 交于点 和点 .①如图2,点 在线段上时,请探究线段 和 之间的数量关系,写出结论并给出证明;
②如图3,点 在线段 的延长线上时, 交射线 于点 ;若 ,直接写出线段 的长度.
22. 我们知道:如图①,点 把线段 分成两部分,如果 .那么称点 为线段 的黄金分割点.它们的比值为 . (1)、在图①中,若 ,则 的长为 ;(2)、如图②,用边长为 的正方形纸片进行如下操作:对折正方形 得折痕 ,连接 ,将 折叠到 上,点 对应点 ,得折痕 .试说明 是 的黄金分割点;(3)、如图③,小明进一步探究:在边长为 的正方形 的边 上任取点 ,连接 ,作 ,交 于点 ,延长 、 交于点 .他发现当 与 满足某种关系时 、 恰好分别是 、 的黄金分割点.请猜想小明的发现,并说明理由.23. 某数学兴趣小组运用《几何画板》软件探究y=ax2(a>0)型抛物线图象.发现:如图1所示,该类型图象上任意一点M到定点 F(0,)的距离MF,始终等于它到定直线l:y=﹣上的距离MN(该结论不需要证明),他们称:定点F为图象的焦点,定直线l为图象的准线,y=﹣叫做抛物线的准线方程.其中原点O为FH的中点,FH=2OF= , 例如,抛物线y=x2 , 其焦点坐标为F(0,),准线方程为l:y=﹣.其中MF=MN,FH=2OH=1.
(1)、在图①中,若 ,则 的长为 ;(2)、如图②,用边长为 的正方形纸片进行如下操作:对折正方形 得折痕 ,连接 ,将 折叠到 上,点 对应点 ,得折痕 .试说明 是 的黄金分割点;(3)、如图③,小明进一步探究:在边长为 的正方形 的边 上任取点 ,连接 ,作 ,交 于点 ,延长 、 交于点 .他发现当 与 满足某种关系时 、 恰好分别是 、 的黄金分割点.请猜想小明的发现,并说明理由.23. 某数学兴趣小组运用《几何画板》软件探究y=ax2(a>0)型抛物线图象.发现:如图1所示,该类型图象上任意一点M到定点 F(0,)的距离MF,始终等于它到定直线l:y=﹣上的距离MN(该结论不需要证明),他们称:定点F为图象的焦点,定直线l为图象的准线,y=﹣叫做抛物线的准线方程.其中原点O为FH的中点,FH=2OF= , 例如,抛物线y=x2 , 其焦点坐标为F(0,),准线方程为l:y=﹣.其中MF=MN,FH=2OH=1.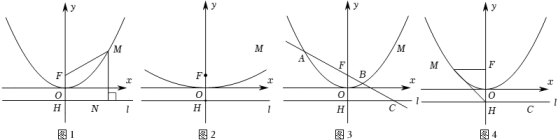 (1)、【基础训练】
(1)、【基础训练】请分别直接写出抛物线y=2x2的焦点坐标和准线l的方程: , .
(2)、【技能训练】如图2所示,已知抛物线y=x2上一点P到准线l的距离为6,求点P的坐标;
(3)、【能力提升】如图3所示,已知过抛物线y=ax2(a>0)的焦点F的直线依次交抛物线及准线l于点A、B、C.若BC=2BF,AF=4,求a的值;
(4)、【拓展升华】古希腊数学家欧多克索斯在深入研究比例理论时,提出了分线段的“中末比”问题:点C将一条线段AB分为两段AC和CB,使得其中较长一段AC是全线段AB与另一段CB的比例中项,即满足:==.后人把这个数称为“黄金分割”把点C称为线段AB的黄金分割点.
如图4所示,抛物线y=x2的焦点F(0,1),准线l与y轴交于点H(0,﹣1),E为线段HF的黄金分割点,点M为y轴左侧的抛物线上一点.当=时,请直接写出△HME的面积值.
24. 在△ABC中,∠BAC=90°,AB=AC,直线l经过点A,过点B、C分别作l的垂线,垂足分别为点D、E. (1)、特例体验:如图①,若直线l∥BC,AB=AC= ,分别求出线设BD、CE和DE的长;(2)、规律探究:
(1)、特例体验:如图①,若直线l∥BC,AB=AC= ,分别求出线设BD、CE和DE的长;(2)、规律探究:(Ⅰ)如图②,若直线l从图①状态开始绕点A旋转α(0<α<45°),请探究线段BD、CE和DE的数量关系并说明理由;
(Ⅱ)如图③,若直线l从图①状态开始绕点A顺时针旋转α(45°<α<90°),与线段BC相交于点H,请再探线段BD、CE和DE的数量关系并说明理由;
(3)、尝试应用:在图③中,延长线设BD交线段AC于点F,若CE=3,DE=1,求S△BFC .
-