浙教版备考2023年中考数学一轮复习78.旋转
试卷更新日期:2023-01-01 类型:一轮复习
一、单选题(每题3分,共30分)
-
1. 下列图形是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下面四幅图是我国一些博物馆的标志,其中既是轴对称图形又是中心对称图形的是( )A、温州博物馆
2. 下面四幅图是我国一些博物馆的标志,其中既是轴对称图形又是中心对称图形的是( )A、温州博物馆 B、西藏博物馆
B、西藏博物馆 C、广东博物馆
C、广东博物馆 D、湖北博物馆
D、湖北博物馆 3. 雪花、风车….展示着中心对称的美,利用中心对称,可以探索并证明图形的性质,请思考在下列图形中,是中心对称图形但不一定是轴对称图形的为( )A、扇形 B、平行四边形 C、等边三角形 D、矩形4. 如图,将△ABC先向右平移1个单位,再绕点P按顺时针方向旋转90°,得到△A′B′C′,则点B的对应点B′的坐标是( )
3. 雪花、风车….展示着中心对称的美,利用中心对称,可以探索并证明图形的性质,请思考在下列图形中,是中心对称图形但不一定是轴对称图形的为( )A、扇形 B、平行四边形 C、等边三角形 D、矩形4. 如图,将△ABC先向右平移1个单位,再绕点P按顺时针方向旋转90°,得到△A′B′C′,则点B的对应点B′的坐标是( ) A、(4,0) B、(2,﹣2) C、(4,﹣1) D、(2,﹣3)5. 如图,在平面直角坐标系中,点B、C、E在y轴上,点C的坐标为(0,1),AC=2,Rt△ODE是Rt△ABC经过某些变换得到的,则正确的变换是( )
A、(4,0) B、(2,﹣2) C、(4,﹣1) D、(2,﹣3)5. 如图,在平面直角坐标系中,点B、C、E在y轴上,点C的坐标为(0,1),AC=2,Rt△ODE是Rt△ABC经过某些变换得到的,则正确的变换是( )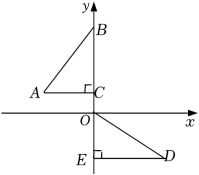 A、△ABC绕点C逆时针旋转90°,再向下平移1个单位 B、△ABC绕点C顺时针旋转90°,再向下平移1个单位 C、△ABC绕点C逆时针旋转90°,再向下平移3个单位 D、△ABC绕点C顺时针旋转90°,再向下平移3个单位6. 在平面直角坐标系中,直线与轴交于点 , 与轴交于点 , 将绕点逆时针旋转到如图的位置,的对应点恰好落在直线上,连接 , 则的长度为( )
A、△ABC绕点C逆时针旋转90°,再向下平移1个单位 B、△ABC绕点C顺时针旋转90°,再向下平移1个单位 C、△ABC绕点C逆时针旋转90°,再向下平移3个单位 D、△ABC绕点C顺时针旋转90°,再向下平移3个单位6. 在平面直角坐标系中,直线与轴交于点 , 与轴交于点 , 将绕点逆时针旋转到如图的位置,的对应点恰好落在直线上,连接 , 则的长度为( )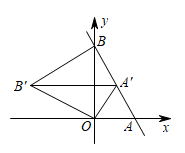 A、 B、 C、2 D、7. 如图,正方形的边长为 , 将正方形绕原点O顺时针旋转45°,则点B的对应点的坐标为( )
A、 B、 C、2 D、7. 如图,正方形的边长为 , 将正方形绕原点O顺时针旋转45°,则点B的对应点的坐标为( )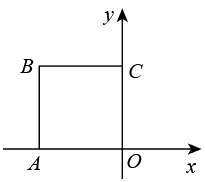 A、 B、 C、 D、8. 如图,中, , 将绕点顺时针旋转得到 , 使点的对应点恰好落在边上,、交于点 . 若 , 则的度数是(用含的代数式表示)( )
A、 B、 C、 D、8. 如图,中, , 将绕点顺时针旋转得到 , 使点的对应点恰好落在边上,、交于点 . 若 , 则的度数是(用含的代数式表示)( )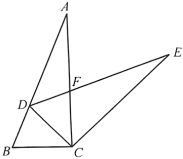 A、 B、 C、 D、9. 如图,在 中, ,将 绕点A逆时针旋转 ,得到 ,连接 并延长交AB于点D,当 时, 的长是( )
A、 B、 C、 D、9. 如图,在 中, ,将 绕点A逆时针旋转 ,得到 ,连接 并延长交AB于点D,当 时, 的长是( )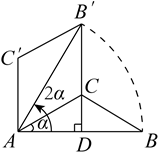 A、 B、 C、 D、10. 如图,在平面直角坐标系中,点P在反比例函数( , )的图象上,其纵坐标为2,过点P作//轴,交x轴于点Q,将线段绕点Q顺时针旋转60°得到线段 . 若点M也在该反比例函数的图象上,则k的值为( )
A、 B、 C、 D、10. 如图,在平面直角坐标系中,点P在反比例函数( , )的图象上,其纵坐标为2,过点P作//轴,交x轴于点Q,将线段绕点Q顺时针旋转60°得到线段 . 若点M也在该反比例函数的图象上,则k的值为( )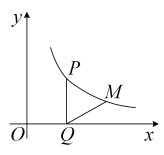 A、 B、 C、 D、4
A、 B、 C、 D、4二、填空题(每题3分,共24分)
-
11. 在平面直角坐标系中,已知点P(﹣3,5)与点Q(3,m﹣2)关于原点对称,则m= .12. 如图,在△ABC中,∠C=90°,∠B=30°,AB=6,将△ABC绕点A逆时针方向旋转15°得到△AB′C′,B′C′交AB于点E,则B′E= .
 13. 如图,在矩形ABCD中,BC=2AB,点P为边AD上的一个动点,线段BP绕点B顺时针旋转60°得到线段BP',连接PP' ,CP'.当点P' 落在边BC上时,∠PP'C的度数为; 当线段CP' 的长度最小时,∠PP'C的度数为
13. 如图,在矩形ABCD中,BC=2AB,点P为边AD上的一个动点,线段BP绕点B顺时针旋转60°得到线段BP',连接PP' ,CP'.当点P' 落在边BC上时,∠PP'C的度数为; 当线段CP' 的长度最小时,∠PP'C的度数为 14. 第二十四届北京冬奥会入场式引导牌上的图案融入了中国结和雪花两种元素.如图,这个图案绕着它的中心旋转角后能够与它本身重合,则角可以为度.(写出一个即可)
14. 第二十四届北京冬奥会入场式引导牌上的图案融入了中国结和雪花两种元素.如图,这个图案绕着它的中心旋转角后能够与它本身重合,则角可以为度.(写出一个即可)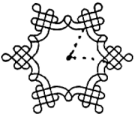 15. 如图,点 , , 都在方格纸的格点上, 绕点 顺时针方向旋转 后得到 ,则点 运动的路径 的长为.
15. 如图,点 , , 都在方格纸的格点上, 绕点 顺时针方向旋转 后得到 ,则点 运动的路径 的长为.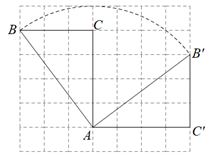 16. 如图,在平面直角坐标系xOy中,点A的坐标为(0,4),P是x轴上一动点,把线段PA绕点P顺时针旋转60°得到线段PF,连接OF,则线段OF长的最小值是 .
16. 如图,在平面直角坐标系xOy中,点A的坐标为(0,4),P是x轴上一动点,把线段PA绕点P顺时针旋转60°得到线段PF,连接OF,则线段OF长的最小值是 .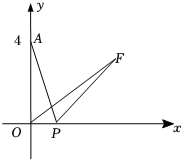
三、解答题(共9题,共72分)
-
17. 已知一次函数y1=ax﹣1(a为常数)与x轴交于点A,与反比例函数y2= 交于B、C两点,B点的横坐标为﹣2.
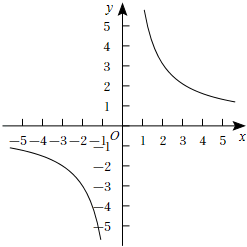 (1)、求出一次函数的解析式并在图中画出它的图象;(2)、求出点C的坐标,并根据图象写出当y1<y2时对应自变量x的取值范围;(3)、若点B与点D关于原点成中心对称,求出△ACD的面积.18. 如图,方格纸上每个小正方形的边长均为1个单位长度,△ABC的顶点A、B、C都在格点上(两条网格线的交点叫格点).请仅用无刻度的直尺按下列要求画图,并保留画图痕迹(不要求写画法).
(1)、求出一次函数的解析式并在图中画出它的图象;(2)、求出点C的坐标,并根据图象写出当y1<y2时对应自变量x的取值范围;(3)、若点B与点D关于原点成中心对称,求出△ACD的面积.18. 如图,方格纸上每个小正方形的边长均为1个单位长度,△ABC的顶点A、B、C都在格点上(两条网格线的交点叫格点).请仅用无刻度的直尺按下列要求画图,并保留画图痕迹(不要求写画法).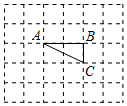 (1)、将△ABC绕点A按顺时针方向旋转90°,点B的对应点为B1,点C的对应点为C1 , 画出△AB1C1;(2)、连接CC1 , △ACC1的面积为;(3)、在线段CC1上画一点D,使得△ACD的面积是△ACC1面积的 .19. 下面是小明关于“对称与旋转的关系”的探究过程,请你补充完整.
(1)、将△ABC绕点A按顺时针方向旋转90°,点B的对应点为B1,点C的对应点为C1 , 画出△AB1C1;(2)、连接CC1 , △ACC1的面积为;(3)、在线段CC1上画一点D,使得△ACD的面积是△ACC1面积的 .19. 下面是小明关于“对称与旋转的关系”的探究过程,请你补充完整.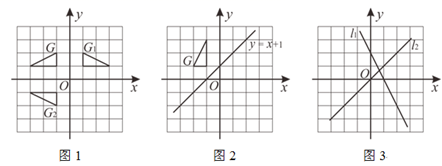 (1)、三角形在平面直角坐标系中的位置如图1所示,简称G , G关于y轴的对称图形为 ,关于 轴的对称图形为 .则将图形 绕点顺时针旋转度,可以得到图形 .(2)、在图2中分别画出G关于y轴和直线 的对称图形 , . 将图形 绕 点(用坐标表示)顺时针旋转 度,可以得到图形 .(3)、综上,如图3,直线 和 所夹锐角为 ,如果图形G关于直线 的对称图形为 ,关于直线 的对称图形为 ,那么将图形 绕点(用坐标表示)顺时针旋转度(用 表示),可以得到图形 .20. 如图1,图2,图3的网格均由边长为1的小正方形组成,图1是三国时期吴国的数学家赵爽所绘制的“弦图”,它由四个形状、大小完全相同的直角三角形组成,赵爽利用这个“弦图”对勾股定理作出了证明,是中国古代数学的一项重要成就,请根据下列要求解答问题.
(1)、三角形在平面直角坐标系中的位置如图1所示,简称G , G关于y轴的对称图形为 ,关于 轴的对称图形为 .则将图形 绕点顺时针旋转度,可以得到图形 .(2)、在图2中分别画出G关于y轴和直线 的对称图形 , . 将图形 绕 点(用坐标表示)顺时针旋转 度,可以得到图形 .(3)、综上,如图3,直线 和 所夹锐角为 ,如果图形G关于直线 的对称图形为 ,关于直线 的对称图形为 ,那么将图形 绕点(用坐标表示)顺时针旋转度(用 表示),可以得到图形 .20. 如图1,图2,图3的网格均由边长为1的小正方形组成,图1是三国时期吴国的数学家赵爽所绘制的“弦图”,它由四个形状、大小完全相同的直角三角形组成,赵爽利用这个“弦图”对勾股定理作出了证明,是中国古代数学的一项重要成就,请根据下列要求解答问题.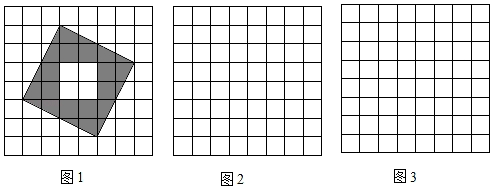 (1)、图1中的“弦图”的四个直角三角形组成的图形是对称图形(填“轴”或“中心”).(2)、请将“弦图”中的四个直角三角形通过你所学过的图形变换,在图2,3的方格纸中设计另外两个不同的图案,画图要求:
(1)、图1中的“弦图”的四个直角三角形组成的图形是对称图形(填“轴”或“中心”).(2)、请将“弦图”中的四个直角三角形通过你所学过的图形变换,在图2,3的方格纸中设计另外两个不同的图案,画图要求:①每个直角三角形的顶点均在方格纸的格点上,且四个三角形互不重叠,不必涂阴影;
②图2中所设计的图案(不含方格纸)必须是轴对称图形而不是中心对称图形;图3中所设计的图案(不含方格纸)必须既是轴对称图形,又是中心对称图形.
21. 阅读下列材料,完成相应学习任务旋转对称
把正n边形绕着它的中心旋转的整数倍后所得的正n边形重合.我们说,正n边形关于其中心有的旋转对称.一般地,如果一个图形绕着某点O旋转角α(0<α<360°)后所得到的图形与原图形重合,则称此图形关于点O有角α的旋转对称.图1就是具有旋转对称性质的一些图形.


任务:
(1)、如图2,正六边形关于其中心O有的旋转对称,中心对称图形关于其对称中心有的旋转对称;(2)、图3是利用旋转变换设计的具有旋转对称性的一个图形,将该图形绕其中心至少旋转与原图形重合;(3)、请以图4为基本图案,在图5中利用平移、轴对称或旋转进行图案设计,使得设计出的图案是中心对称图形.22. 已知点在正方形的对角线上,正方形与正方形有公共点 .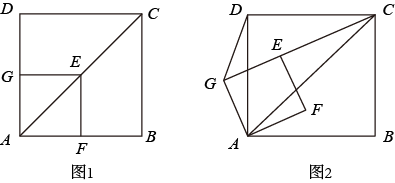 (1)、如图1,当点在上,在上,求的值为多少;(2)、将正方形绕点逆时针方向旋转 , 如图2,求:的值为多少;(3)、 , , 将正方形绕逆时针方向旋转 , 当 , , 三点共线时,请直接写出的长度.23. 如图①所示,将一个边长为2的正方形和一个长为2、宽为1的长方形拼在一起,构成一个大的长方形 . 现将小长方形绕点C顺时针旋转至长方形 , 旋转角为 .
(1)、如图1,当点在上,在上,求的值为多少;(2)、将正方形绕点逆时针方向旋转 , 如图2,求:的值为多少;(3)、 , , 将正方形绕逆时针方向旋转 , 当 , , 三点共线时,请直接写出的长度.23. 如图①所示,将一个边长为2的正方形和一个长为2、宽为1的长方形拼在一起,构成一个大的长方形 . 现将小长方形绕点C顺时针旋转至长方形 , 旋转角为 .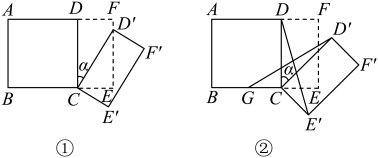 (1)、当点恰好落在边上时,求旋转角的值;(2)、如图②,G为中点,且 , 求证:;(3)、小长方形绕点C顺时针旋转一周的过程中,与能否全等?若能,直接写出旋转角的值;若不能,说明理由.24. 综合与实践
(1)、当点恰好落在边上时,求旋转角的值;(2)、如图②,G为中点,且 , 求证:;(3)、小长方形绕点C顺时针旋转一周的过程中,与能否全等?若能,直接写出旋转角的值;若不能,说明理由.24. 综合与实践某学校的数学兴趣小组发现这样一个模型,两个顶角相等的等腰三角形,如果具有公共的顶角的顶点,并把它们的底角顶点连接起来,会形成一组全等的三角形,具有这个规律的图形称为“手拉手”图形.
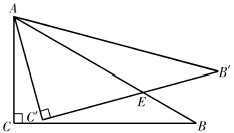
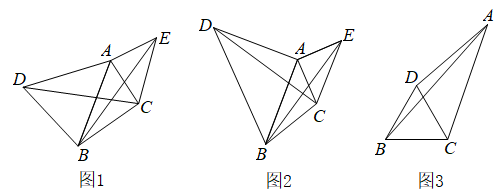 (1)、[材料理解]如图1,在中,分别以 , 为边向外作等腰和等腰 . , , , 连接 , , 试猜想与的大小关系,并说明理由;(2)、[深入探究]如图2,在中, , , , 分别以 , 为边向外作等腰直角和等腰直角 , , 连接 , , 求的长.(3)、[延伸应用]如图3,在中, , 点D为平面内一点,连接 , , 满足 , , , , 求的长.25. 探究题∶
(1)、[材料理解]如图1,在中,分别以 , 为边向外作等腰和等腰 . , , , 连接 , , 试猜想与的大小关系,并说明理由;(2)、[深入探究]如图2,在中, , , , 分别以 , 为边向外作等腰直角和等腰直角 , , 连接 , , 求的长.(3)、[延伸应用]如图3,在中, , 点D为平面内一点,连接 , , 满足 , , , , 求的长.25. 探究题∶ (1)、特殊情景:如图(1),在四边形ABCD中,AB=AD,以点A为顶点作一个角,角的两边分别交BC,CD于点E,F,且∠EAF=∠BAD,连接EF,若∠BAD=∠B=∠D=90°,探究:线段BE,DF,EF之间的数量关系,并说明理由(2)、类比猜想:类比特殊情景,在上述(1)条件下,把“∠BAD=∠B=∠D=90°”改成一股情况“∠BAD=α , ∠B+∠D=180°,”如图(2),小明猜想:线段BE,DF,EF之间的数量关系是否仍然成立?若成立,请你写出结论;若不成立,请你写出成立时α的取值范围.(3)、解决问题:如图(3),在△ABC中,∠BAC=90°,AB=AC=4,点D,E均在边BC上,且∠DAE=45°,若BD= , 计算DE的长度.
(1)、特殊情景:如图(1),在四边形ABCD中,AB=AD,以点A为顶点作一个角,角的两边分别交BC,CD于点E,F,且∠EAF=∠BAD,连接EF,若∠BAD=∠B=∠D=90°,探究:线段BE,DF,EF之间的数量关系,并说明理由(2)、类比猜想:类比特殊情景,在上述(1)条件下,把“∠BAD=∠B=∠D=90°”改成一股情况“∠BAD=α , ∠B+∠D=180°,”如图(2),小明猜想:线段BE,DF,EF之间的数量关系是否仍然成立?若成立,请你写出结论;若不成立,请你写出成立时α的取值范围.(3)、解决问题:如图(3),在△ABC中,∠BAC=90°,AB=AC=4,点D,E均在边BC上,且∠DAE=45°,若BD= , 计算DE的长度.