浙教版备考2023年中考数学一轮复习77.平移
试卷更新日期:2023-01-01 类型:一轮复习
一、单选题(每题3分,共30分)
-
1. 2022北京冬残奥会的会徽是以汉字“飞”为灵感来设计的,展现了运动员不断飞跃,超越自我,奋力拼搏,激励世界的冬残奥精神下列的四个图中,能由如图所示的会徽经过平移得到的是( )
 A、
A、 B、
B、 C、
C、 D、
D、 2. 如图,△ABC沿BC方向平移后的像为△DEF,已知BC=5,EC=2,则平移的距离是( )
2. 如图,△ABC沿BC方向平移后的像为△DEF,已知BC=5,EC=2,则平移的距离是( )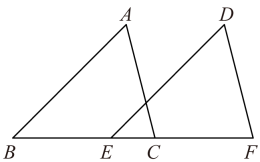 A、1 B、2 C、3 D、43. 将点先向右平移5个单位长度,再向下平移6个单位长度得到的点的坐标是( )A、 B、 C、 D、4. 如图,点 , 将线段先向上平移2个单位长度,再向左平移3个单位长度,得到线段 , 则点的对应点的坐标是( )
A、1 B、2 C、3 D、43. 将点先向右平移5个单位长度,再向下平移6个单位长度得到的点的坐标是( )A、 B、 C、 D、4. 如图,点 , 将线段先向上平移2个单位长度,再向左平移3个单位长度,得到线段 , 则点的对应点的坐标是( )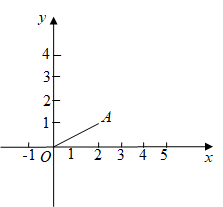 A、 B、 C、 D、5. 如图,现有一把直尺和一块三角尺,其中 , , AB=8,点A对应直尺的刻度为12.将该三角尺沿着直尺边缘平移,使得△ABC移动到 , 点对应直尺的刻度为0,则四边形的面积是( )
A、 B、 C、 D、5. 如图,现有一把直尺和一块三角尺,其中 , , AB=8,点A对应直尺的刻度为12.将该三角尺沿着直尺边缘平移,使得△ABC移动到 , 点对应直尺的刻度为0,则四边形的面积是( )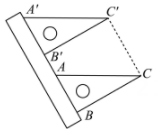 A、96 B、 C、192 D、6. 如图,点 , 将线段平移得到线段 , 若 , 则点D的坐标是( )
A、96 B、 C、192 D、6. 如图,点 , 将线段平移得到线段 , 若 , 则点D的坐标是( )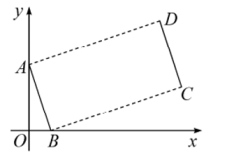 A、 B、 C、 D、7. 如图,将 沿 边向右平移得到 , 交 于点G.若 . .则 的值为( )
A、 B、 C、 D、7. 如图,将 沿 边向右平移得到 , 交 于点G.若 . .则 的值为( ) A、2 B、4 C、6 D、88. 一个数a在数轴上表示的点是A,当点A在数轴上向左移动了6个单位长度后到点B,点A与点B表示的数恰好互为相反数,则数a是( )A、-3 B、-6 C、6 D、39. 在Rt△ABC中,∠ABC=90°,AC=13,AB=12,则图中五个小直角三角形的周长之和为( )
A、2 B、4 C、6 D、88. 一个数a在数轴上表示的点是A,当点A在数轴上向左移动了6个单位长度后到点B,点A与点B表示的数恰好互为相反数,则数a是( )A、-3 B、-6 C、6 D、39. 在Rt△ABC中,∠ABC=90°,AC=13,AB=12,则图中五个小直角三角形的周长之和为( )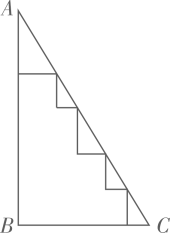 A、25 B、18 C、17 D、3010. 如图,将直角沿边的方向平移到的位置,连结 , 若14,则的长为( )
A、25 B、18 C、17 D、3010. 如图,将直角沿边的方向平移到的位置,连结 , 若14,则的长为( )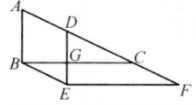 A、4 B、6 C、8 D、12
A、4 B、6 C、8 D、12二、填空题(每题4分,共24分)
-
11. 已知△A′B′O′是由△ABO平移得到的,点A的坐标为(-1,2),它的对应点A'的坐标为(3,4),△ABO内任意一点P(a,b)平移后的对应点P'的坐标为 .12. 如图,某住宅小区内有一长方形地块,想在长方形地块内修筑同样宽的两条小路图中阴影部分 , 余下部分绿化,小路的宽为 , 则绿化面积为 .
 13. 如图,将扇形AOB沿OB方向平移,使点O移到OB的中点 处,得到扇形 .若∠O=90°,OA=2,则阴影部分的面积为.
13. 如图,将扇形AOB沿OB方向平移,使点O移到OB的中点 处,得到扇形 .若∠O=90°,OA=2,则阴影部分的面积为. 14. 如图,线段AB两端点的坐标分别为A(-1,0),B(1,1),把线段AB平移到CD位置,若线段CD两端点的坐标分别为C(1,a),D(b,4),则a+b的值为
14. 如图,线段AB两端点的坐标分别为A(-1,0),B(1,1),把线段AB平移到CD位置,若线段CD两端点的坐标分别为C(1,a),D(b,4),则a+b的值为 15. 如图(1),△ABC和△A′B′C′是两个边长不相等的等边三角形,点B′、C′、B、C都在直线l上,△ABC固定不动,将△A′B′C′在直线l上自左向右平移.开始时,点C′与点B重合,当点B′移动到与点C重合时停止.设△A′B′C′移动的距离为x,两个三角形重叠部分的面积为y,y与x之间的函数关系如图(2)所示,则△ABC的边长是.
15. 如图(1),△ABC和△A′B′C′是两个边长不相等的等边三角形,点B′、C′、B、C都在直线l上,△ABC固定不动,将△A′B′C′在直线l上自左向右平移.开始时,点C′与点B重合,当点B′移动到与点C重合时停止.设△A′B′C′移动的距离为x,两个三角形重叠部分的面积为y,y与x之间的函数关系如图(2)所示,则△ABC的边长是.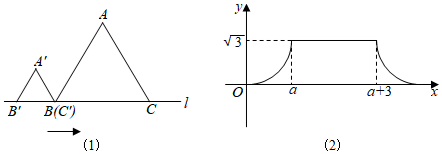 16. 如图:在直角坐标系中,设一动点自处向上运动1个单位至 , 然后向左运动2个单位至处,再向下运动3个单位至处,再向右运动4个单位至处,再向上运动5个单位至处,如此继续运动下去.设 , , 2,3…,则 .
16. 如图:在直角坐标系中,设一动点自处向上运动1个单位至 , 然后向左运动2个单位至处,再向下运动3个单位至处,再向右运动4个单位至处,再向上运动5个单位至处,如此继续运动下去.设 , , 2,3…,则 .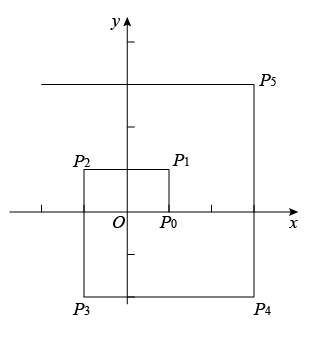
三、解答题(共7题,共66分)
-
17. 已知 ,
 (1)、画出向下平移4个单位的三角形;(2)、画出关于y轴对称的三角形;(3)、求的面积.18. 如图,△ABC是边长为2的等边三角形,将△ABC沿BC平移到△DCE的位置,连接BD交AC于F,求△ABC平移的距离和BF的长.
(1)、画出向下平移4个单位的三角形;(2)、画出关于y轴对称的三角形;(3)、求的面积.18. 如图,△ABC是边长为2的等边三角形,将△ABC沿BC平移到△DCE的位置,连接BD交AC于F,求△ABC平移的距离和BF的长. 19. 如图,平面直角坐标系中,△ABC的顶点都在网格点上,其中A点坐标为(-1,4).
19. 如图,平面直角坐标系中,△ABC的顶点都在网格点上,其中A点坐标为(-1,4). (1)、写出点B,C的坐标:B( , ),C( , );(2)、要将△ABC完全平移到第四象限(不含坐标轴),且顶点都在网格点上,至少需要将此三角形向(填“左”或“右”)平移个单位长度,再向(填“上”或“下”)平移个单位长度.若此时位置记作 , 则的三个顶点坐标分别是A'( , ),B'( , ),C'( , ).(3)、已知是由△ABC平移得到的,A点的对应点 , B点对应点 , 当和两点坐标满足和时,请直接写出是由△ABC经过怎样的平移得到的.20. 如图,点 在抛物线C: 上,且在C的对称轴右侧.
(1)、写出点B,C的坐标:B( , ),C( , );(2)、要将△ABC完全平移到第四象限(不含坐标轴),且顶点都在网格点上,至少需要将此三角形向(填“左”或“右”)平移个单位长度,再向(填“上”或“下”)平移个单位长度.若此时位置记作 , 则的三个顶点坐标分别是A'( , ),B'( , ),C'( , ).(3)、已知是由△ABC平移得到的,A点的对应点 , B点对应点 , 当和两点坐标满足和时,请直接写出是由△ABC经过怎样的平移得到的.20. 如图,点 在抛物线C: 上,且在C的对称轴右侧.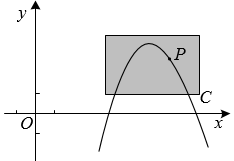 (1)、写出C的对称轴和y的最大值,并求a的值;(2)、坐标平面上放置一透明胶片,并在胶片上描画出点P及C的一段,分别记为 , .平移该胶片,使 所在抛物线对应的函数恰为 .求点 移动的最短路程.21. 如图,已知一次函数y1=kx+b的图象与函数y2=(x>0)的图象交于A(6,-),B( , n)两点,与y轴交于点C,将直线AB沿y轴向上平移t个单位长度得到直线DE,DE与y轴交于点F.
(1)、写出C的对称轴和y的最大值,并求a的值;(2)、坐标平面上放置一透明胶片,并在胶片上描画出点P及C的一段,分别记为 , .平移该胶片,使 所在抛物线对应的函数恰为 .求点 移动的最短路程.21. 如图,已知一次函数y1=kx+b的图象与函数y2=(x>0)的图象交于A(6,-),B( , n)两点,与y轴交于点C,将直线AB沿y轴向上平移t个单位长度得到直线DE,DE与y轴交于点F.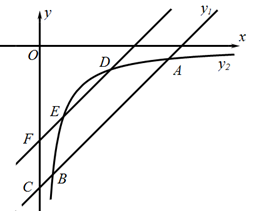 (1)、求y1与y2的解析式;(2)、观察图象,直接写出y1<y2时x的取值范围;(3)、连接AD,CD,若△ACD的面积为6,则t的值为.22. 一次函数的图象与轴交于点 , 二次函数的图象经过点、原点和一次函数图象上的点 .
(1)、求y1与y2的解析式;(2)、观察图象,直接写出y1<y2时x的取值范围;(3)、连接AD,CD,若△ACD的面积为6,则t的值为.22. 一次函数的图象与轴交于点 , 二次函数的图象经过点、原点和一次函数图象上的点 .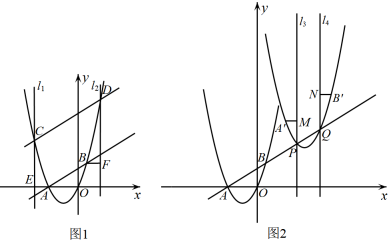 (1)、求这个二次函数的表达式;(2)、如图1,一次函数与二次函数的图象交于点、(),过点作直线轴于点 , 过点作直线轴,过点作于点 .
(1)、求这个二次函数的表达式;(2)、如图1,一次函数与二次函数的图象交于点、(),过点作直线轴于点 , 过点作直线轴,过点作于点 .①▲ , ▲ (分别用含的代数式表示);
②证明:;
(3)、如图2,二次函数的图像是由二次函数的图像平移后得到的,且与一次函数的图像交于点、(点在点的左侧),过点作直线轴,过点作直线轴,设平移后点、的对应点分别为、 , 过点作于点 , 过点作于点 .①与相等吗?请说明你的理由;
②若 , 求的值.
23. 已知: , 在中, , , 点在上,边在上,在中, , 边在直线上,; (1)、如图1,求的度数;(2)、如图2,将沿射线的方向平移,当点在上时,求度数;(3)、如图3,将沿射线的方向平移到的位置,若点是的中点, , 则平移的距离为 .(4)、将在直线上平移,当以、、为顶点的三角形是直角三角形时,请直接写出度数.
(1)、如图1,求的度数;(2)、如图2,将沿射线的方向平移,当点在上时,求度数;(3)、如图3,将沿射线的方向平移到的位置,若点是的中点, , 则平移的距离为 .(4)、将在直线上平移,当以、、为顶点的三角形是直角三角形时,请直接写出度数.