浙教版备考2023年中考数学一轮复习76.轴对称
试卷更新日期:2023-01-01 类型:一轮复习
一、单选题(每题3分,共30分)
-
1. 下列图形中是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列图案是轴对称图形但不是中心对称图形的是( )A、
2. 下列图案是轴对称图形但不是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 3. 在平面直角坐标系中,点关于y轴对称的点的坐标是( )A、 B、 C、 D、4. 下列汉字中,能看成轴对称图形的是( )A、坡 B、上 C、草 D、原5. 如图,菱形ABCD的边长为2,点P是对角线AC上的一个动点,点E、F分别为边AD、DC的中点,则PE + PF的最小值是( )
3. 在平面直角坐标系中,点关于y轴对称的点的坐标是( )A、 B、 C、 D、4. 下列汉字中,能看成轴对称图形的是( )A、坡 B、上 C、草 D、原5. 如图,菱形ABCD的边长为2,点P是对角线AC上的一个动点,点E、F分别为边AD、DC的中点,则PE + PF的最小值是( ) A、2 B、 C、1.5 D、6. 如图,一束光线 先后经平面镜 , 反射后,反射光线 与 平行,当 时, 的度数为( )
A、2 B、 C、1.5 D、6. 如图,一束光线 先后经平面镜 , 反射后,反射光线 与 平行,当 时, 的度数为( ) A、 B、 C、 D、7. 将一个等腰三角形纸板沿垂线段 , 进行剪切,得到三角形 , 再按如图2方式拼放,其中与共线.若 , 则的长为( )
A、 B、 C、 D、7. 将一个等腰三角形纸板沿垂线段 , 进行剪切,得到三角形 , 再按如图2方式拼放,其中与共线.若 , 则的长为( ) A、 B、 C、 D、78. 明明和亮亮一起下五子棋,明明持黑棋,亮亮持白棋.如图,若棋盘正中间的白棋的位置用表示,最右上角的黑棋的位置用表示,明明把第七枚圆形棋子放在适当位置,使所有棋子组成轴对称图形、则第七枚圆形棋子放的位置不可能是( )
A、 B、 C、 D、78. 明明和亮亮一起下五子棋,明明持黑棋,亮亮持白棋.如图,若棋盘正中间的白棋的位置用表示,最右上角的黑棋的位置用表示,明明把第七枚圆形棋子放在适当位置,使所有棋子组成轴对称图形、则第七枚圆形棋子放的位置不可能是( ) A、 B、 C、 D、9. 如图,直线l,m相交于点O,P为这两直线外一点,且OP=2.7.若点P关于直线l,m的对称点分别是点P1 , P2 , 则P1 , P2之间的距离可能是( )
A、 B、 C、 D、9. 如图,直线l,m相交于点O,P为这两直线外一点,且OP=2.7.若点P关于直线l,m的对称点分别是点P1 , P2 , 则P1 , P2之间的距离可能是( ) A、0 B、5 C、6 D、710. 如图,在中, , , 点在上,过点作交于点 , 现将沿着所在的直线折叠,使得点落在点处, , 分别交于点、若:: , 则图中阴影部分的周长为( )
A、0 B、5 C、6 D、710. 如图,在中, , , 点在上,过点作交于点 , 现将沿着所在的直线折叠,使得点落在点处, , 分别交于点、若:: , 则图中阴影部分的周长为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每题4分,共24分)
-
11. 如图是一个轴对称图形,若 , 则 .
 12. 有背面完全相同,正面分别画有等腰三角形、平行四边形、矩形、菱形、等腰梯形的卡片5张,现正面朝下放置在桌面上,将其混合后,并从中随机抽取一张,则抽中正面的图形一定是轴对称图形的卡片的概率为.13. 点A(a,b)和B关于x轴对称,而点B与点C(2,3)关于y轴对称,那么,ab=.14. 如图,与图中直线y=﹣x+1关于x轴对称的直线的函数表达式是 .
12. 有背面完全相同,正面分别画有等腰三角形、平行四边形、矩形、菱形、等腰梯形的卡片5张,现正面朝下放置在桌面上,将其混合后,并从中随机抽取一张,则抽中正面的图形一定是轴对称图形的卡片的概率为.13. 点A(a,b)和B关于x轴对称,而点B与点C(2,3)关于y轴对称,那么,ab=.14. 如图,与图中直线y=﹣x+1关于x轴对称的直线的函数表达式是 . 15. 如图,将矩形纸片ABCD折叠,折痕为MN,点M,N分别在边AD,BC上,点C,D的对应点分别在E,F且点F在矩形内部,MF的延长线交BC与点G,EF交边BC于点H. , , 当点H为GN三等分点时,MD的长为 .
15. 如图,将矩形纸片ABCD折叠,折痕为MN,点M,N分别在边AD,BC上,点C,D的对应点分别在E,F且点F在矩形内部,MF的延长线交BC与点G,EF交边BC于点H. , , 当点H为GN三等分点时,MD的长为 .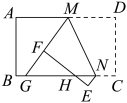 16. 已知正方形的边长为4,为上一点,连接并延长交的延长线于点 , 过点作 , 交于点 , 交于点 , 为的中点,为上一动点,分别连接 , . 若 , 则的最小值为 .
16. 已知正方形的边长为4,为上一点,连接并延长交的延长线于点 , 过点作 , 交于点 , 交于点 , 为的中点,为上一动点,分别连接 , . 若 , 则的最小值为 .
三、解答题(共8题,共66分)
-
17. 图①,图②均是的正方形网格,每个小正方形的顶点称为格点.其中点 , , 均在格点上.请在给定的网格中按要求画四边形.
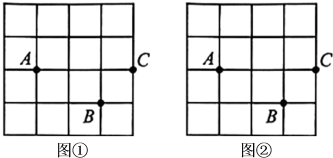 (1)、在图①中,找一格点 , 使以点 , , , 为顶点的四边形是轴对称图形;(2)、在图②中,找一格点 , 使以点 , , , 为顶点的四边形是中心对称图形.18. 如图是由16个小正方形组成的正方形网格图,现已将其中的两个涂黑.请你用四种不同的方法分别在下图中再涂黑三个空白的小正方形,使整个图形成为轴对称图形.
(1)、在图①中,找一格点 , 使以点 , , , 为顶点的四边形是轴对称图形;(2)、在图②中,找一格点 , 使以点 , , , 为顶点的四边形是中心对称图形.18. 如图是由16个小正方形组成的正方形网格图,现已将其中的两个涂黑.请你用四种不同的方法分别在下图中再涂黑三个空白的小正方形,使整个图形成为轴对称图形. 19. 在平面直角坐标系中,各顶点坐标分别为: , , .
19. 在平面直角坐标系中,各顶点坐标分别为: , , .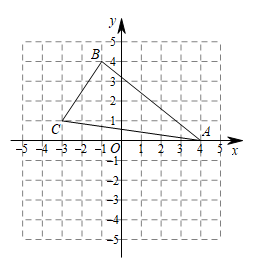 (1)、在图中作 , 使和关于x轴对称;(2)、已知与关于y轴对称,写出点 , , 的坐标;(3)、求的面积.20. 在平面直角坐标系中,抛物线y=﹣ +(m﹣1)x+2m与x轴交于A,B(4,0)两点,与y轴交于点C,点P是抛物线在第一象限内的一个动点.
(1)、在图中作 , 使和关于x轴对称;(2)、已知与关于y轴对称,写出点 , , 的坐标;(3)、求的面积.20. 在平面直角坐标系中,抛物线y=﹣ +(m﹣1)x+2m与x轴交于A,B(4,0)两点,与y轴交于点C,点P是抛物线在第一象限内的一个动点.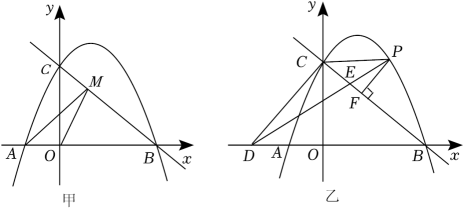 (1)、求抛物线的解析式,并直接写出点A,C的坐标;(2)、如图甲,点M是直线BC上的一个动点,连接AM,OM,是否存在点M使AM+OM最小,若存在,请求出点M的坐标,若不存在,请说明理由;(3)、如图乙,过点P作PF⊥BC,垂足为F,过点C作CD⊥BC,交x轴于点D,连接DP交BC于点E,连接CP.设△PEF的面积为S1 , △PEC的面积为S2 , 是否存在点P,使得最大,若存在,请求出点P的坐标,若不存在,请说明理由.21. 如图,为等腰三角形, , , 点为的中点,过作于点点为射线上一点,为线段上一点不与点 , 重合 , 连结.
(1)、求抛物线的解析式,并直接写出点A,C的坐标;(2)、如图甲,点M是直线BC上的一个动点,连接AM,OM,是否存在点M使AM+OM最小,若存在,请求出点M的坐标,若不存在,请说明理由;(3)、如图乙,过点P作PF⊥BC,垂足为F,过点C作CD⊥BC,交x轴于点D,连接DP交BC于点E,连接CP.设△PEF的面积为S1 , △PEC的面积为S2 , 是否存在点P,使得最大,若存在,请求出点P的坐标,若不存在,请说明理由.21. 如图,为等腰三角形, , , 点为的中点,过作于点点为射线上一点,为线段上一点不与点 , 重合 , 连结. (1)、求 , 的长.(2)、若 , 将点绕点逆时针旋转 , 得到点 , 当点落在的一边上时,求的长.(3)、当点与点重合时,在线段上取点 , 使点、关于成轴对称,求点到的距离.22. 已知抛物线 与 轴交于 , 两点,与 轴交于点 .
(1)、求 , 的长.(2)、若 , 将点绕点逆时针旋转 , 得到点 , 当点落在的一边上时,求的长.(3)、当点与点重合时,在线段上取点 , 使点、关于成轴对称,求点到的距离.22. 已知抛物线 与 轴交于 , 两点,与 轴交于点 .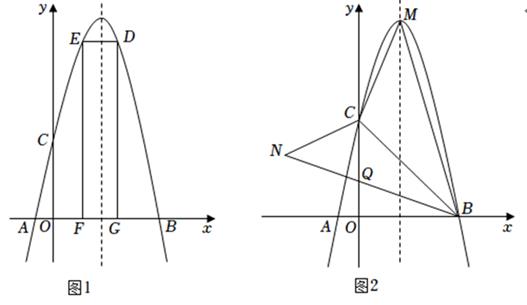 (1)、求 , , 的值;(2)、如图 ,点 是抛物线上位于对称轴右侧的一个动点,且点 在第一象限内,过点 作 轴的平行线交抛物线于点 ,作 轴的平行线交 轴于点 ,过点 作 轴,垂足为点 ,当四边形 的周长最大时,求点 的坐标;(3)、如图 ,点 是抛物线的顶点,将 沿 翻折得到 , 与 轴交于点 ,在对称轴上找一点 ,使得 是以 为直角边的直角三角形,求出所有符合条件的点 的坐标.23. 已知函数y= 的图象如图所示,点A(x1 , y1)在第一象限内的函数图象上.
(1)、求 , , 的值;(2)、如图 ,点 是抛物线上位于对称轴右侧的一个动点,且点 在第一象限内,过点 作 轴的平行线交抛物线于点 ,作 轴的平行线交 轴于点 ,过点 作 轴,垂足为点 ,当四边形 的周长最大时,求点 的坐标;(3)、如图 ,点 是抛物线的顶点,将 沿 翻折得到 , 与 轴交于点 ,在对称轴上找一点 ,使得 是以 为直角边的直角三角形,求出所有符合条件的点 的坐标.23. 已知函数y= 的图象如图所示,点A(x1 , y1)在第一象限内的函数图象上.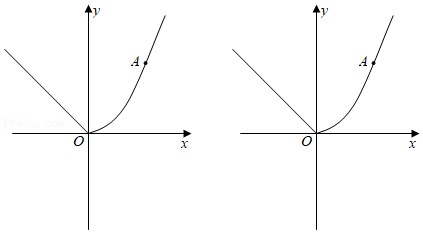 (1)、若点B(x2 , y2)也在上述函数图象上,满足x2<x1.
(1)、若点B(x2 , y2)也在上述函数图象上,满足x2<x1.①当y2=y1=4时,求x1 , x2的值;
②若|x2|=|x1|,设w=y1﹣y2 , 求w的最小值;
(2)、过A点作y轴的垂线AP,垂足为P,点P关于x轴的对称点为P′,过A点作x轴的垂线AQ,垂足为Q,Q关于直线AP′的对称点为Q′,直线AQ′是否与y轴交于某定点?若是,求出这个定点的坐标;若不是,请说明理由.24. 综合与实践,【问题情境】:数学活动课上,老师出示了一个问题:如图1,在正方形ABCD中,E是BC的中点, ,EP与正方形的外角 的平分线交于P点.试猜想AE与EP的数量关系,并加以证明;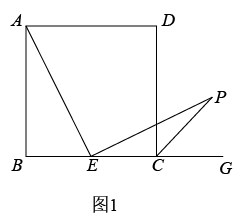
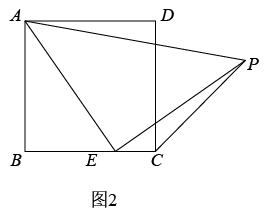
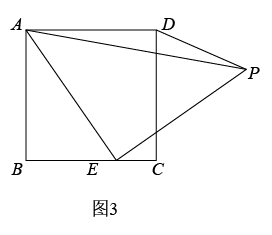 (1)、【思考尝试】同学们发现,取AB的中点F,连接EF可以解决这个问题.请在图1中补全图形,解答老师提出的问题.(2)、【实践探究】希望小组受此问题启发,逆向思考这个题目,并提出新的问题:如图2,在正方形ABCD中,E为BC边上一动点(点E,B不重合), 是等腰直角三角形, ,连接CP,可以求出 的大小,请你思考并解答这个问题.(3)、【拓展迁移】突击小组深入研究希望小组提出的这个问题,发现并提出新的探究点:如图3,在正方形ABCD中,E为BC边上一动点(点E,B不重合), 是等腰直角三角形, ,连接DP.知道正方形的边长时,可以求出 周长的最小值.当 时,请你求出 周长的最小值.
(1)、【思考尝试】同学们发现,取AB的中点F,连接EF可以解决这个问题.请在图1中补全图形,解答老师提出的问题.(2)、【实践探究】希望小组受此问题启发,逆向思考这个题目,并提出新的问题:如图2,在正方形ABCD中,E为BC边上一动点(点E,B不重合), 是等腰直角三角形, ,连接CP,可以求出 的大小,请你思考并解答这个问题.(3)、【拓展迁移】突击小组深入研究希望小组提出的这个问题,发现并提出新的探究点:如图3,在正方形ABCD中,E为BC边上一动点(点E,B不重合), 是等腰直角三角形, ,连接DP.知道正方形的边长时,可以求出 周长的最小值.当 时,请你求出 周长的最小值.