浙教版备考2023年中考数学一轮复习75.命题与证明
试卷更新日期:2023-01-01 类型:一轮复习
一、单选题(每题3分,共30分)
-
1. 下列命题中,是真命题的有( )
①对角线相等且互相平分的四边形是矩形②对角线互相垂直的四边形是菱形③四边相等的四边形是正方形④四边相等的四边形是菱形
A、①② B、①④ C、②③ D、③④2. 下列说法正确的是( )A、命题一定有逆命题 B、所有的定理一定有逆定理 C、真命题的逆命题一定是真命题 D、假命题的逆命题一定是假命题3. 下列命题错误的是( )A、经过直线外一点,有且只有一条直线与这条直线平行 B、负数的立方根是负数 C、对角线互相垂直的四边形是菱形 D、五边形的外角和是4. 下列命题:①;②数据1,3,3,5的方差为2;③因式分解;④平分弦的直径垂直于弦;⑤若使代数式在实数范围内有意义,则 . 其中假命题的个数是( )A、1 B、3 C、2 D、45. 以下命题:①面包店某种面包售价元/个,因原材料涨价,面包价格上涨10%,会员优惠从打八五折调整为打九折,则会员购买一个面包比涨价前多花了元;②等边三角形中,是边上一点,是边上一点,若 , 则;③两边及第三边上的中线对应相等的两个三角形全等;④一列自然数0,1,2,3,55,依次将该列数中的每一个数平方后除以100,得到一列新数,则原数与对应新数的差,随着原数的增大而增大.其中真命题的个数有( )A、1个 B、2个 C、3个 D、4个6. 下列命题中是假命题的是( )A、三角形的中位线平行于三角形的第三边,并且等于第三边的一半 B、如果两个角互为邻补角,那么这两个角一定相等 C、从圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角 D、直角三角形斜边上的中线等于斜边的一半7. 下列选项中,能说明命题“若a≤1,则a2≤1”是假命题的反例是( )A、a=2 B、a=1 C、a=-1 D、a=-28. 能说明命题“对于任何实数a,都有|a|=a”是假命题的反例是( )A、a=-2 B、 C、a=1 D、9. 对于一元二次方程(a≠0),下列命题中错误的是( )A、a+b+c=0,则 B、若方程有两个不相等的实根,则方程必有两个不相等的实根 C、若c是方程的一个根,则一定有ac+b+1=0成立 D、若x0是一元二次方程的根,则10. 下列说法:①三角形三条高相交于一点;②两边和一角对应相等的两个三角形全等;③有一个角是 , 并且两腰分别相等的两个等腰三角形全等;④到三角形三个顶点距离相等的点是三角形三条角平分线的交点;⑤等腰三角形一腰上的高与底边的夹角等于顶角的一半.其中正确的有( )
A、1个 B、2个 C、3 D、4二、填空题(每题4分,共24分)
-
11. 请写出命题“如果 ,那么 ”的逆命题:.12. 把命题:对顶角相等.改写“如果那么”的形式为: .13. 命题“三角形的三个内角中至少有两个锐角”是(填“真命题”或“假命题”).14. 在说明命题“若|a|>3,则a>3”是假命题的反例中,a的值可以是 .15. ①若ab>0,则a>0,b>0;
②一个角的补角大于这个角;
③两直线平行,同位角相等;
④有两边和其中一边的对角对应相等的两个三角形全等;
⑤点P坐标为(-2,6),将其先向右平移6个单位,再向下平移8个单位,得到点P1 , 坐标为(4,-2).
其中是真命题的有.
16. 请写出命题“四条边相等的四边形是菱形”的逆命题: , 逆命题是一个(填真命题或假命题).三、解答题(共8题,共66分)
-
17. 求证:顶角是锐角的等腰三角形腰上的高与底边夹角等于其顶角的一半.
 (1)、根据题意补全下图,并根据题设和结论,结合图形,用符号语言补充写出“已知”和“求证”.
(1)、根据题意补全下图,并根据题设和结论,结合图形,用符号语言补充写出“已知”和“求证”.已知:在锐角中, , ▲ ;
求证: ▲ .
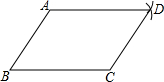
(2)、证明:18. 嘉淇同学要证明命题“两组对边分别相等的四边形是平行四边形”是正确的,她先用尺规作出了如图的四边形ABCD,并写出了如下不完整的已知和求证.(1)、在方框中填空,以补全已知和求证;已知:如图,在四边形ABCD中,
BC=AD,
AB= .
求证:四边形ABCD是四边形.
 (2)、按嘉淇的想法写出证明:
(2)、按嘉淇的想法写出证明:证明:
 (3)、用文字叙述所证命题的逆命题为 .19. 如图,现有以下三个条件:①②③.请你以其中两个作为题设,另一个作为结论构造命题.
(3)、用文字叙述所证命题的逆命题为 .19. 如图,现有以下三个条件:①②③.请你以其中两个作为题设,另一个作为结论构造命题. (1)、你构造的是哪几个命题?(2)、你构造的命题是真命题还是假命题?若是真命题,请给予证明;若是假命题,请举出反例(证明其中的一个命题即可).20. 已知:如图,AB是⊙O的直径,AC是⊙O的弦,过点C的直线交AB延长线于点D,给出下列信息:
(1)、你构造的是哪几个命题?(2)、你构造的命题是真命题还是假命题?若是真命题,请给予证明;若是假命题,请举出反例(证明其中的一个命题即可).20. 已知:如图,AB是⊙O的直径,AC是⊙O的弦,过点C的直线交AB延长线于点D,给出下列信息:①∠A=30°;
②CD是⊙O的切线;
③OB=BD.
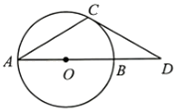 (1)、请在上述3条信息中选择其中两条作为条件,剩下的一条作为结论.你选择的条件是 ▲ , 结论是 ▲ (只要填写序号).判断结论是否正确,并说明理由;(2)、在(1)的条件下,若CD=3 , 求的长度.21. 下面是小明设计“作圆的一个内接矩形,并使其对角线夹角为 ”尺规作图的过程.
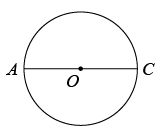
(1)、请在上述3条信息中选择其中两条作为条件,剩下的一条作为结论.你选择的条件是 ▲ , 结论是 ▲ (只要填写序号).判断结论是否正确,并说明理由;(2)、在(1)的条件下,若CD=3 , 求的长度.21. 下面是小明设计“作圆的一个内接矩形,并使其对角线夹角为 ”尺规作图的过程.已知:如图, .
求作:矩形 ,使矩形 内接于 ,对角线 与 的夹角为
作法:①作 的直径 ;
②以点A为圆心, 长为半径作弧.交直线 上方的圆于点B;
③连接 并延长交 于点D;
④顺次连接 、 、 和 .
四边形 就是所求作的矩形,
根据小明设计的尺规作图过程
 (1)、使用直尺和圆规,补全图形(保留作图痕迹);(2)、完成下面的证明.
(1)、使用直尺和圆规,补全图形(保留作图痕迹);(2)、完成下面的证明.证明:∵点A,C都在 上,
, .
∴四边形 是平行四边形.( )(填推理依据).
又 是 的直径,
( )(填推理依据).
∴四边形 是矩形.
又 ▲ .
是等边三角形.
∴四边形 是所求作的矩形.
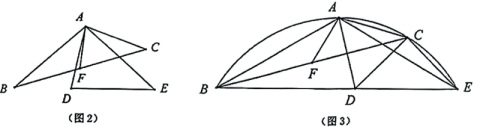
22. 如图,在△ABC中,点D,E分别在AB,AC上. (1)、若BD=CE,CD=BE,求证AB=AC;(2)、分别将“BD=CE”记为①,“CD=BE”记为②,“AB=AC”记为③.以①、③为条件,②为结论构成命题1,以②、③为条件,①为结论构成命题2.则命题1是命题,命题2是命题(选择“真”或“假“填入空格)23. 如果两个三角形的两边对应相等,且它们的夹角互补,那么这两个三角形叫做互补三角形.如图1,的中线,则和就是互补三角形.
(1)、若BD=CE,CD=BE,求证AB=AC;(2)、分别将“BD=CE”记为①,“CD=BE”记为②,“AB=AC”记为③.以①、③为条件,②为结论构成命题1,以②、③为条件,①为结论构成命题2.则命题1是命题,命题2是命题(选择“真”或“假“填入空格)23. 如果两个三角形的两边对应相等,且它们的夹角互补,那么这两个三角形叫做互补三角形.如图1,的中线,则和就是互补三角形.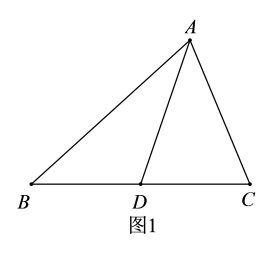
 (1)、根据定义判断下面两个命题的真假(填“真”或“假”)
(1)、根据定义判断下面两个命题的真假(填“真”或“假”)①互补三角形一定不全等.命题
②互补三角形的面积相等.命题
(2)、如图2,和为互补三角形,是的中线.求证:;
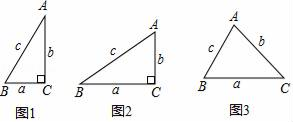
(3)、如图3,在(2)的条件下,若三点共线,连结CE, , 四边形为圆内接四边形.当时,求的值.24. 阅读材料,回答问题:小聪学完了“锐角三角函数”的相关知识后,通过研究发现:如图1,在Rt△ABC中,如果∠C=90°,∠=30°,BC═a=1,AC=b= , AB=c=2,那么==2.通过上网查阅资料,他又知“sin90°=1”,因此他得到“在含30°角的直角三角形中,存在着==的关系.
这个关系对于一般三角形还适用吗?为此他做了如下的探究:
(1)、如图2,在R△ABC中,∠C=90°,BC=a,AC=b,AB=C,请判断此时“==”的关系是否成立?答:(2)、完成上述探究后,他又想“对于任意的锐角△ABC,上述关系还成立吗?”因此他又继续进行了如下的探究:如图3,在锐角△ABC中,BC=a,AC=b,AB=c,请判断此时“ ==”的关系是否成立?并证明你的判断.(提示:过点C作CD⊥AB于D,过点A作AH⊥BC,再结合定义或其它方法证明).