浙教版备考2023年中考数学一轮复习74.圆的综合
试卷更新日期:2023-01-01 类型:一轮复习
一、单选题(每题3分,共30分)
-
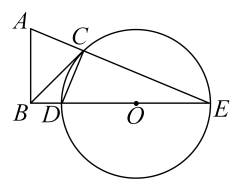
1. 如图所示,已知三角形为直角三角形,为圆切线,为切点,则和面积之比为( )
 A、 B、 C、 D、2. 如图,AB是⊙O的弦,等边三角形OCD的边CD与⊙O相切于点P,连接OA,OB,OP,AD.若∠COD+∠AOB=180°, AB=6,则AD的长是( )
A、 B、 C、 D、2. 如图,AB是⊙O的弦,等边三角形OCD的边CD与⊙O相切于点P,连接OA,OB,OP,AD.若∠COD+∠AOB=180°, AB=6,则AD的长是( )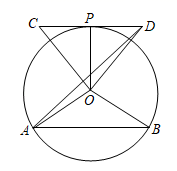 A、6 B、3 C、2 D、3. 如图,已知 , , , 与 、 均相切,点P是线段 与抛物线 的交点,则a的值为( )
A、6 B、3 C、2 D、3. 如图,已知 , , , 与 、 均相切,点P是线段 与抛物线 的交点,则a的值为( )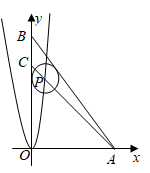 A、4 B、 C、 D、54. 如图,在矩形中, , , 为矩形内一点, , 连接 , 则的最小值为( )
A、4 B、 C、 D、54. 如图,在矩形中, , , 为矩形内一点, , 连接 , 则的最小值为( )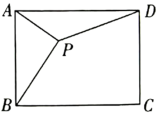 A、8 B、 C、10 D、5. 在Rt△ABC中,∠C=90°,AC=10,BC=12,点D为线段BC上一动点.以CD为⊙O直径,作AD交⊙O于点E,连BE,则BE的最小值为( )
A、8 B、 C、10 D、5. 在Rt△ABC中,∠C=90°,AC=10,BC=12,点D为线段BC上一动点.以CD为⊙O直径,作AD交⊙O于点E,连BE,则BE的最小值为( ) A、6 B、8 C、10 D、126. 如图,AB是半圆O的直径,点C在半圆O上,OA=10,BC=16,D是弧AC上一个动点,连接BD,过点C作CM⊥BD,连接AM,在点D移动的过程中,AM的最小值为( )
A、6 B、8 C、10 D、126. 如图,AB是半圆O的直径,点C在半圆O上,OA=10,BC=16,D是弧AC上一个动点,连接BD,过点C作CM⊥BD,连接AM,在点D移动的过程中,AM的最小值为( )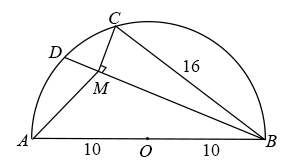 A、 B、 C、 D、7. 如图,在平面直角坐标系中,A(0,3)、B(3,0),以点B为圆心、2为半径的⊙B上有一动点P.连接AP,若点C为AP的中点,连接OC,则OC的最小值为( )
A、 B、 C、 D、7. 如图,在平面直角坐标系中,A(0,3)、B(3,0),以点B为圆心、2为半径的⊙B上有一动点P.连接AP,若点C为AP的中点,连接OC,则OC的最小值为( )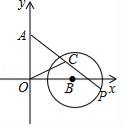 A、1 B、2﹣1 C、 D、﹣18. 如图, △ABC是⊙O的内接三角形,将劣弧AC沿AC折叠后刚好经过弦BC 的中点 D.若 AC=6,∠C=60°,则⊙O的半径长为( )
A、1 B、2﹣1 C、 D、﹣18. 如图, △ABC是⊙O的内接三角形,将劣弧AC沿AC折叠后刚好经过弦BC 的中点 D.若 AC=6,∠C=60°,则⊙O的半径长为( ) A、 B、 C、 D、9. 如图,正比例函数y=2x与反比例函数的图象交于A、B两点,点P在以为圆心,1为半径的⊙C上运动,点Q是AP的中点,则OQ长的最大值为( )
A、 B、 C、 D、9. 如图,正比例函数y=2x与反比例函数的图象交于A、B两点,点P在以为圆心,1为半径的⊙C上运动,点Q是AP的中点,则OQ长的最大值为( ) A、2 B、 C、 D、10. 已知:如图,为的直径,为的切线,D、B为切点,交于点E,的延长线交于点F,连接 . 以下结论:①;②点E为的内心;③;④ . 其中正确的只有( )
A、2 B、 C、 D、10. 已知:如图,为的直径,为的切线,D、B为切点,交于点E,的延长线交于点F,连接 . 以下结论:①;②点E为的内心;③;④ . 其中正确的只有( ) A、①② B、②③④ C、①③④ D、①②④
A、①② B、②③④ C、①③④ D、①②④二、填空题(每题4分,共24分)
-
11. 如图是以点O为圆心,AB为直径的圆形纸片.点C在⊙O上,将该圆形纸片沿直线CO对折,点B落在⊙O上的点D处(不与点A重合),连接CB,CD,AD.设CD与直径AB交于点E.若AD=ED,则∠B=度; 的值等于 .
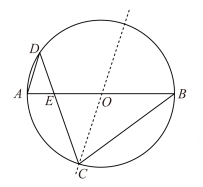 12. 如图,AB,CD是的弦,且 , 连接OA,OB,OC,OD,AD,BC.若 , , , 则AD的长是 .
12. 如图,AB,CD是的弦,且 , 连接OA,OB,OC,OD,AD,BC.若 , , , 则AD的长是 . 13. 如图,是的外接圆,为直径,若 , , 点从点出发,在内运动且始终保持 , 当 , 两点距离最小时,动点的运动路径长为 .
13. 如图,是的外接圆,为直径,若 , , 点从点出发,在内运动且始终保持 , 当 , 两点距离最小时,动点的运动路径长为 . 14. 如图,在扇形AOB中,点C,D在 上,将 沿弦CD折叠后恰好与OA,OB相切于点E,F. 已知∠AOB=120°,OA=6,则 的度数为 , 折痕CD的长为 .
14. 如图,在扇形AOB中,点C,D在 上,将 沿弦CD折叠后恰好与OA,OB相切于点E,F. 已知∠AOB=120°,OA=6,则 的度数为 , 折痕CD的长为 .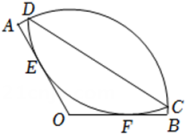 15. 如图,、 , 以为直径作 , 射线交于、两点,为弧的中点,为的中点.当射线绕点旋转时,的最小值为 .
15. 如图,、 , 以为直径作 , 射线交于、两点,为弧的中点,为的中点.当射线绕点旋转时,的最小值为 .
三、解答题(共8题,共66分)
-
16. 如图,在矩形ABCD中,以AB的中点O为圆心,以OA为半径作半圆,连接OD交半圆于点E,在上取点F,使 , 连接BF,DF.
 (1)、求证:DF与半圆相切;(2)、如果AB=10,BF=6,求矩形ABCD的面积.17. 如图,AB为⊙O的直径,C为圆上的一点,D为劣弧的中点,过点D作⊙O的切线与AC的延长线交于点P,与AB的延长线交于点F,AD与BC交于点E.
(1)、求证:DF与半圆相切;(2)、如果AB=10,BF=6,求矩形ABCD的面积.17. 如图,AB为⊙O的直径,C为圆上的一点,D为劣弧的中点,过点D作⊙O的切线与AC的延长线交于点P,与AB的延长线交于点F,AD与BC交于点E.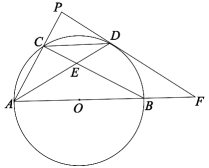 (1)、求证:;(2)、若⊙O的半径为 , DE=1,求AE的长度;(3)、在(2)的条件下,求的面积.18. 在平面直角坐标系中,已知点对于点给出如下定义:将点向右或向左平移个单位长度,再向上或向下平移个单位长度,得到点 , 点关于点的对称点为 , 称点为点的“对应点”.(1)、如图,点点在线段的延长线上,若点点为点的“对应点”.
(1)、求证:;(2)、若⊙O的半径为 , DE=1,求AE的长度;(3)、在(2)的条件下,求的面积.18. 在平面直角坐标系中,已知点对于点给出如下定义:将点向右或向左平移个单位长度,再向上或向下平移个单位长度,得到点 , 点关于点的对称点为 , 称点为点的“对应点”.(1)、如图,点点在线段的延长线上,若点点为点的“对应点”.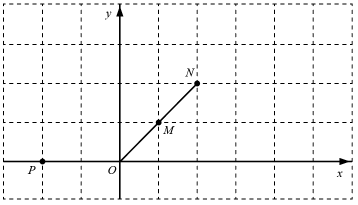
①在图中画出点;
②连接交线段于点求证:
(2)、的半径为1,是上一点,点在线段上,且 , 若为外一点,点为点的“对应点”,连接当点在上运动时直接写出长的最大值与最小值的差(用含的式子表示)19. 一个玻璃球体近似半圆为直径,半圆上点处有个吊灯的中点为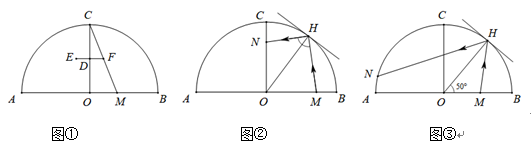 (1)、如图①,为一条拉线,在上,求的长度.(2)、如图②,一个玻璃镜与圆相切,为切点,为上一点,为入射光线,为反射光线,求的长度.(3)、如图③,是线段上的动点,为入射光线,为反射光线交圆于点在从运动到的过程中,求点的运动路径长.20. 筒车是我国古代利用水力驱动的灌溉工具,车轮缚以竹简,旋转时低则舀水,高则泻水.如图,水力驱动筒车按逆时针方向转动,竹筒把水引至A处,水沿射线方向泻至水渠 , 水渠所在直线与水面平行;设筒车为 , 与直线交于P,Q两点,与直线交于B,C两点,恰有 , 连接 .
(1)、如图①,为一条拉线,在上,求的长度.(2)、如图②,一个玻璃镜与圆相切,为切点,为上一点,为入射光线,为反射光线,求的长度.(3)、如图③,是线段上的动点,为入射光线,为反射光线交圆于点在从运动到的过程中,求点的运动路径长.20. 筒车是我国古代利用水力驱动的灌溉工具,车轮缚以竹简,旋转时低则舀水,高则泻水.如图,水力驱动筒车按逆时针方向转动,竹筒把水引至A处,水沿射线方向泻至水渠 , 水渠所在直线与水面平行;设筒车为 , 与直线交于P,Q两点,与直线交于B,C两点,恰有 , 连接 .
 (1)、求证:为的切线;(2)、筒车的半径为 , . 当水面上升,A,O,Q三点恰好共线时,求筒车在水面下的最大深度(精确到 , 参考值:).21. 如图,四边形ABCD中, ,∠ABC=90°,∠C=30°,AD=3, ,DH⊥BC于点H . 将△PQM与该四边形按如图方式放在同一平面内,使点P与A重合,点B在PM上,其中∠Q=90°,∠QPM=30°, .
(1)、求证:为的切线;(2)、筒车的半径为 , . 当水面上升,A,O,Q三点恰好共线时,求筒车在水面下的最大深度(精确到 , 参考值:).21. 如图,四边形ABCD中, ,∠ABC=90°,∠C=30°,AD=3, ,DH⊥BC于点H . 将△PQM与该四边形按如图方式放在同一平面内,使点P与A重合,点B在PM上,其中∠Q=90°,∠QPM=30°, .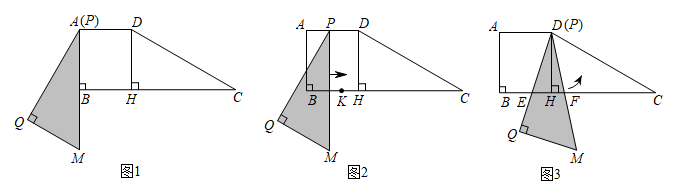 (1)、求证:△PQM≌△CHD;(2)、△PQM从图1的位置出发,先沿着BC方向向右平移(图2),当点P到达点D后立刻绕点D逆时针旋转(图3),当边PM旋转50°时停止.
(1)、求证:△PQM≌△CHD;(2)、△PQM从图1的位置出发,先沿着BC方向向右平移(图2),当点P到达点D后立刻绕点D逆时针旋转(图3),当边PM旋转50°时停止.①边PQ从平移开始,到绕点D旋转结束,求边PQ扫过的面积;
②如图2,点K在BH上,且 .若△PQM右移的速度为每秒1个单位长,绕点D旋转的速度为每秒5°,求点K在△PQM区域(含边界)内的时长;
③如图3.在△PQM旋转过程中,设PQ , PM分别交BC于点E , F , 若BE=d , 直接写出CF的长(用含d的式子表示).
22. 操作探究题(1)、已知是半圆的直径,(是正整数,且不是3的倍数)是半圆的一个圆心角.操作:如图1,分别将半圆的圆心角(取1、4、5、10)所对的弧三等分(要求:仅用圆规作图,不写作法,保留作图痕迹);

交流:当时,可以仅用圆规将半圆的圆心角所对的弧三等分吗?
探究:你认为当满足什么条件时,就可以仅用圆规将半圆的圆心角所对的弧三等分?说说你的理由.
(2)、如图2,的圆周角 . 为了将这个圆的圆周14等分,请作出它的一条14等分弧(要求:仅用圆规作图,不写作法,保留作图痕迹).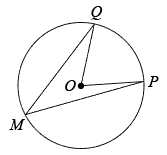 23. 如图,在网格中,每个小正方形的边长均为1,每个小正方形的顶点称为格点,点、、、、均为格点.
23. 如图,在网格中,每个小正方形的边长均为1,每个小正方形的顶点称为格点,点、、、、均为格点.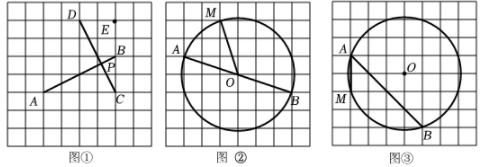 (1)、【操作探究】在数学活动课上,佳佳同学在如图①的网格中,用无刻度的直尺画了两条互相垂直的线段、 , 相交于点并给出部分说理过程,请你补充完整:
(1)、【操作探究】在数学活动课上,佳佳同学在如图①的网格中,用无刻度的直尺画了两条互相垂直的线段、 , 相交于点并给出部分说理过程,请你补充完整:解:在网格中取格点 , 构建两个直角三角形,分别是△ABC和△CDE.
在Rt△ABC中,
在Rt△CDE中, ,
所以.
所以∠=∠.
因为∠∠ =∠ =90°,
所以∠ +∠ =90°,
所以∠ =90°,
即⊥.
(2)、【拓展应用】如图②是以格点为圆心,为直径的圆,请你只用无刻度的直尺,在上找出一点P,使 , 写出作法,并给出证明:(3)、【拓展应用】如图③是以格点为圆心的圆,请你只用无刻度的直尺,在弦上找出一点P.使=· , 写出作法,不用证明.