浙教版备考2023年中考数学一轮复习73.弧长、扇形面积、圆锥、圆柱
试卷更新日期:2023-01-01 类型:一轮复习
一、单选题(每题3分,共30分)
-
1. 已知圆锥的母线长8cm,底面圆的直径6cm,则这个圆锥的侧面积是( )A、96πcm2 B、48πcm2 C、33πcm2 D、24πcm22. 如图1是一块弘扬“社会主义核心价值观”的扇面宣传展板,该展板的部分示意图如图2所示,它是以O为圆心,OA,OB长分别为半径,圆心角 形成的扇面,若 , ,则阴影部分的面积为( )

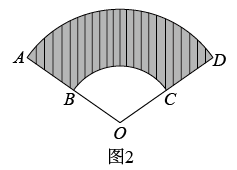 A、 B、 C、 D、3. 用一张半圆形铁皮,围成一个底面半径为的圆锥形工件的侧面(接缝忽略不计),则圆锥的母线长为( )A、 B、 C、 D、4. 一个扇形的弧长是 , 其圆心角是150°,此扇形的面积为( )A、 B、 C、 D、5. 如图.将扇形翻折,使点A与圆心O重合,展开后折痕所在直线l与交于点C,连接 . 若 , 则图中阴影部分的面积是( )
A、 B、 C、 D、3. 用一张半圆形铁皮,围成一个底面半径为的圆锥形工件的侧面(接缝忽略不计),则圆锥的母线长为( )A、 B、 C、 D、4. 一个扇形的弧长是 , 其圆心角是150°,此扇形的面积为( )A、 B、 C、 D、5. 如图.将扇形翻折,使点A与圆心O重合,展开后折痕所在直线l与交于点C,连接 . 若 , 则图中阴影部分的面积是( )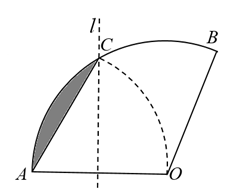 A、 B、 C、 D、6. 如图,边长为的正方形内接于 , , 分别与相切于点和点 , 的延长线与的延长线交于点 , 则图中阴影部分的面积为( )
A、 B、 C、 D、6. 如图,边长为的正方形内接于 , , 分别与相切于点和点 , 的延长线与的延长线交于点 , 则图中阴影部分的面积为( ) A、 B、 C、 D、7. 如图,圆锥底面圆的半径 ,母线长 ,则这个圆锥的侧面积为( )
A、 B、 C、 D、7. 如图,圆锥底面圆的半径 ,母线长 ,则这个圆锥的侧面积为( ) A、 B、 C、 D、8. 如图,AB是⊙O的直径,C是⊙O上一点,连接AC,OC,若AB=6,∠A=30°,则 的长为( )
A、 B、 C、 D、8. 如图,AB是⊙O的直径,C是⊙O上一点,连接AC,OC,若AB=6,∠A=30°,则 的长为( )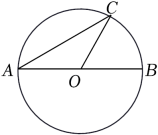 A、6π B、2π C、π D、π9. 蒙古包可以近似地看作由圆锥和圆柱组成.下图是一个蒙古包的示意图,底面圆半径DE=2m,圆锥的高AC=1.5m,圆柱的高CD=2.5m,则下列说法错误的是( )
A、6π B、2π C、π D、π9. 蒙古包可以近似地看作由圆锥和圆柱组成.下图是一个蒙古包的示意图,底面圆半径DE=2m,圆锥的高AC=1.5m,圆柱的高CD=2.5m,则下列说法错误的是( ) A、圆柱的底面积为4πm2 B、圆柱的侧面积为10πm2 C、圆锥的母线AB长为2.25m D、圆锥的侧面积为5πm210. 如图,是的直径,将弦绕点顺时针旋转得到 , 此时点的对应点落在上,延长 , 交于点 , 若 , 则图中阴影部分的面积为( )
A、圆柱的底面积为4πm2 B、圆柱的侧面积为10πm2 C、圆锥的母线AB长为2.25m D、圆锥的侧面积为5πm210. 如图,是的直径,将弦绕点顺时针旋转得到 , 此时点的对应点落在上,延长 , 交于点 , 若 , 则图中阴影部分的面积为( )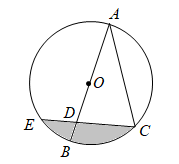 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每题4分,共24分)
-
11. 若圆锥的底面圆半径为2,母线长为5,则该圆锥的侧面积是.(结果保留)12. 如图,边长为4的正方形ABCD内接于 , 则的长是(结果保留)
 13. 如图,等边三角形ABC内接于⊙O,BC=2 , 则图中阴影部分的面积是 .
13. 如图,等边三角形ABC内接于⊙O,BC=2 , 则图中阴影部分的面积是 .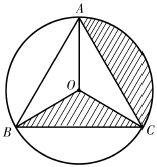 14. 如图,在矩形中, , 将线段绕点按逆时针方向旋转,使得点落在边上的点处,线段扫过的面积为 .
14. 如图,在矩形中, , 将线段绕点按逆时针方向旋转,使得点落在边上的点处,线段扫过的面积为 .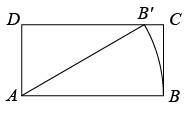 15. 如图,等腰中, , 以A为圆心,以AB为半径作﹔以BC为直径作 . 则图中阴影部分的面积是 . (结果保留)
15. 如图,等腰中, , 以A为圆心,以AB为半径作﹔以BC为直径作 . 则图中阴影部分的面积是 . (结果保留)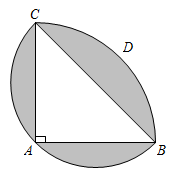 16. 在活动课上,“雄鹰组”用含30°角的直角三角尺设计风车.如图,∠C=90°,∠ABC=30°,AC=2,将直角三角尺绕点A逆时针旋转得到△AB′C′,使点C′落在AB边上,以此方法做下去……则B点通过一次旋转至B′所经过的路径长为 . (结果保留π)
16. 在活动课上,“雄鹰组”用含30°角的直角三角尺设计风车.如图,∠C=90°,∠ABC=30°,AC=2,将直角三角尺绕点A逆时针旋转得到△AB′C′,使点C′落在AB边上,以此方法做下去……则B点通过一次旋转至B′所经过的路径长为 . (结果保留π)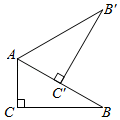
三、解答题(共8题,共66分)
-
17. 在数学实验课上,小莹将含角的直角三角尺分别以两个直角边为轴旋转一周,得到甲、乙两个圆锥,并用作图软件Geogebra画出如下示意图
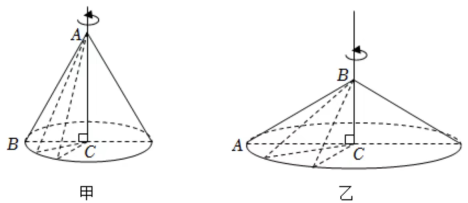
小亮观察后说:“甲、乙圆锥的侧面都是由三角尺的斜边旋转得到,所以它们的侧面积相等.”
你认同小亮的说法吗?请说明理由.
18. 如图,点A、B、C在圆O上,∠ABC=60°,直线AD∥BC,AB=AD,点O在BD上.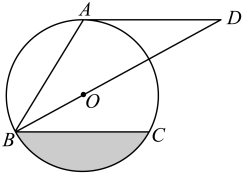 (1)、判断直线AD与圆O的位置关系,并说明理由;(2)、若圆的半径为6,求图中阴影部分的面积.19. 如图①,矩形ABCD与以EF为直径的半圆O在直线l的上方,线段AB与点E、F都在直线l上,且AB=7,EF=10,BC>5. 点B以1个单位/秒的速度从点E处出发,沿射线EF方向运动矩形ABCD随之运动,运动时间为t秒
(1)、判断直线AD与圆O的位置关系,并说明理由;(2)、若圆的半径为6,求图中阴影部分的面积.19. 如图①,矩形ABCD与以EF为直径的半圆O在直线l的上方,线段AB与点E、F都在直线l上,且AB=7,EF=10,BC>5. 点B以1个单位/秒的速度从点E处出发,沿射线EF方向运动矩形ABCD随之运动,运动时间为t秒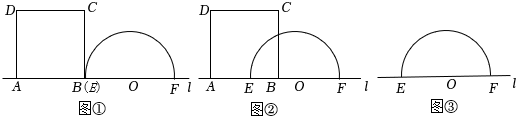 (1)、如图2,当t=2.5时,求半圆O在矩形ABCD内的弧的长度;(2)、在点B运动的过程中,当 AD、BC都与半圆O相交,设这两个交点为G、H连接OG,OH.若∠GOH为直角,求此时t的值.20. 某种冰激凌的外包装可以视为圆锥,它的底面圆直径 与母线 长之比为 .制作这种外包装需要用如图所示的等腰三角形材料,其中 , .将扇形 围成圆锥时, , 恰好重合.
(1)、如图2,当t=2.5时,求半圆O在矩形ABCD内的弧的长度;(2)、在点B运动的过程中,当 AD、BC都与半圆O相交,设这两个交点为G、H连接OG,OH.若∠GOH为直角,求此时t的值.20. 某种冰激凌的外包装可以视为圆锥,它的底面圆直径 与母线 长之比为 .制作这种外包装需要用如图所示的等腰三角形材料,其中 , .将扇形 围成圆锥时, , 恰好重合.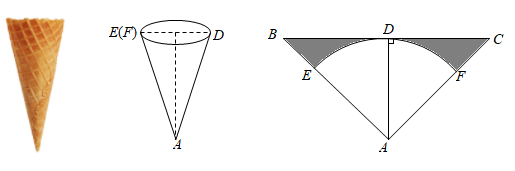 (1)、求这种加工材料的顶角 的大小(2)、若圆锥底面圆的直径 为5cm,求加工材料剩余部分(图中阴影部分)的面积.(结果保留 )21. 综合与实践
(1)、求这种加工材料的顶角 的大小(2)、若圆锥底面圆的直径 为5cm,求加工材料剩余部分(图中阴影部分)的面积.(结果保留 )21. 综合与实践 问题情境:如图,将一个圆锥的侧面展开后可得到一个圆心角为 , 半径为l的扇形 , 圆锥底面是一个半径为r的圆.母线在展开图上对应的半径经过的中点.(1)、特例研究:当 , 时,n= , 展开图上,与OB的夹角为 .(2)、问题提出:求证: .(3)、问题解决:如图2,一种纸质圆锥形生日帽,底面直径为 , 母线长也为 , 为了美观,想在底面圆上一点A和与之相对的母线PB中点C之间拉一条细彩带进行装饰,求彩带长度的最小值.(提示:尝试画出圆锥侧面展开图)22. 用如图所示的甲、乙、丙木板做一个长、宽、高分别为a厘米,b厘米,h厘米的长方体有盖木箱(a>b),其中甲刚好能做成箱底和一个长侧面,乙刚好能做成一个长侧面和一个短侧面,丙刚好能做成箱盖和一个短侧面。
问题情境:如图,将一个圆锥的侧面展开后可得到一个圆心角为 , 半径为l的扇形 , 圆锥底面是一个半径为r的圆.母线在展开图上对应的半径经过的中点.(1)、特例研究:当 , 时,n= , 展开图上,与OB的夹角为 .(2)、问题提出:求证: .(3)、问题解决:如图2,一种纸质圆锥形生日帽,底面直径为 , 母线长也为 , 为了美观,想在底面圆上一点A和与之相对的母线PB中点C之间拉一条细彩带进行装饰,求彩带长度的最小值.(提示:尝试画出圆锥侧面展开图)22. 用如图所示的甲、乙、丙木板做一个长、宽、高分别为a厘米,b厘米,h厘米的长方体有盖木箱(a>b),其中甲刚好能做成箱底和一个长侧面,乙刚好能做成一个长侧面和一个短侧面,丙刚好能做成箱盖和一个短侧面。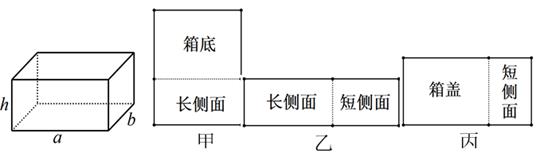 (1)、填空:用含a、b、h的代数式表示以下面积:
(1)、填空:用含a、b、h的代数式表示以下面积:甲的面积;乙的面积;丙的面积.
(2)、当h=20cm时,若甲的面积比丙的面积大200cm2 , 乙的面积为1400cm2 , 求a和b的值;(3)、现将一张长、宽分别为a厘米、b厘米的长方形纸板(如图①)分割成两个小长方形。左侧部分刚好分割成两个最大的等圆,和右侧剩下部分刚好做成一个圆柱体模型(如图②),且这样的圆柱体模型的高刚好与木箱的高相等。问:一个上述长方体木箱中最多可以放个这样的圆柱体模型。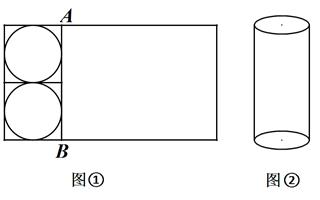 23. 如图1,在平面直角坐标系中,Rt△OAB的直角边OA在y轴的正半轴上,且OA=6,斜边OB=10,点P为线段AB上一动点.
23. 如图1,在平面直角坐标系中,Rt△OAB的直角边OA在y轴的正半轴上,且OA=6,斜边OB=10,点P为线段AB上一动点.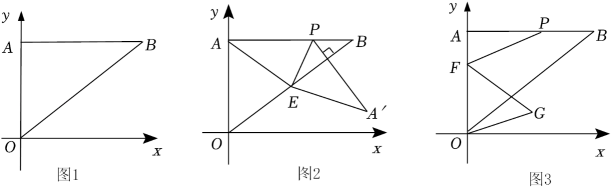 (1)、请直接写出点B的坐标;(2)、若动点P满足∠POB=45°,求此时点P的坐标;(3)、如图2,若点E为线段OB的中点,连接PE,以PE为折痕,在平面内将△APE折叠,点A的对应点为A',当PA'⊥OB时,求此时点P的坐标;(4)、如图3,若F为线段AO上一点,且AF=2,连接FP,将线段FP绕点F顺时针方向旋转60°得线段FG,连接OG,当OG取最小值时,请直接写出OG的最小值和此时线段FP扫过的面积.24. 如图
(1)、请直接写出点B的坐标;(2)、若动点P满足∠POB=45°,求此时点P的坐标;(3)、如图2,若点E为线段OB的中点,连接PE,以PE为折痕,在平面内将△APE折叠,点A的对应点为A',当PA'⊥OB时,求此时点P的坐标;(4)、如图3,若F为线段AO上一点,且AF=2,连接FP,将线段FP绕点F顺时针方向旋转60°得线段FG,连接OG,当OG取最小值时,请直接写出OG的最小值和此时线段FP扫过的面积.24. 如图

【问题情境】
在一次数学兴趣小组活动中,小昕同学将一大一小两个三角板按照如图1所示的方式摆放.其中 , , .
【问题探究】
小昕同学将三角板 绕点 按顺时针方向旋转.
(1)、如图2,当点 落在边 上时,延长 交 于点 ,求 的长.(2)、若点 、 、 在同一条直线上,求点 到直线 的距离.(3)、连接 ,取 的中点 ,三角板 由初始位置(图1),旋转到点 、 、 首次在同一条直线上(如图3),求点 所经过的路径长.(4)、如图4, 为 的中点,则在旋转过程中,点 到直线 的距离的最大值是.