浙教版备考2023年中考数学一轮复习72.圆与多边形
试卷更新日期:2023-01-01 类型:一轮复习
一、单选题(每题3分,共30分)
-
1. 如图,四边形是的内接四边形,若 , 则的度数是( )
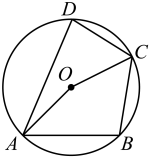 A、 B、 C、 D、
A、 B、 C、 D、 -
2. 如图,四边形是的内接四边形.若 , 则的度数为( )
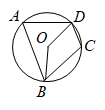 A、138° B、121° C、118° D、112°
A、138° B、121° C、118° D、112° -
3. 如图,正六边形ABCDEF内接于⊙O,半径为6,则这个正六边形的边心距OM和的长分别为( )
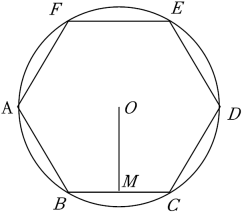 A、4, B、3 , π C、2 , D、3 , 2π
A、4, B、3 , π C、2 , D、3 , 2π -
4. 如图,已知⊙O的周长等于6π,则该圆内接正六边形ABCDEF的边心距OG为( )
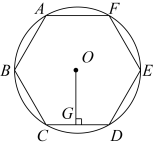 A、3 B、 C、 D、3
A、3 B、 C、 D、3 -
5. 如图,已知正六边形内接于半径为的 , 随机地往内投一粒米,落在正六边形内的概率为( )
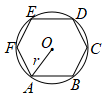 A、 B、 C、 D、以上答案都不对
A、 B、 C、 D、以上答案都不对 -
6. 如图,有一个半径为2的圆形时钟,其中每个刻度间的弧长均相等,过9点和11点的位置作一条线段,则钟面中阴影部分的面积为( )
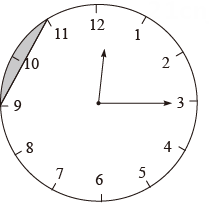 A、 B、 C、 D、
A、 B、 C、 D、 -
7. 如图,点、、、、都是上的点, , , 则的度数为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
8. 如图是一个半径为6cm的的纸片,是的内接三角形,分别以直线和折叠纸片,和都经过圆心O,则图中阴影部分的面积是( )
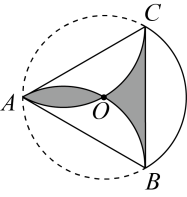 A、 B、 C、 D、
A、 B、 C、 D、 -
9. 如图,点为线段的中点,点 , , 到点的距离相等,则与的数量关系为( )
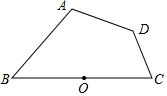 A、 B、 C、 D、
A、 B、 C、 D、 -
10. 我国魏晋时期的数学家刘徽首创割圆术:割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体,而无所失矣",即通过圆内接正多边形割圆,从正六边形开始,每次边数成倍增加,依次可得圆内接正十二边形,内接正二十四边形,…….边数越多割得越细,正多边形的周长就越接近圆的周长.再根据“圆周率等于圆周长与该圆直径的比”来计算圆周率.设圆的半径为R,图1中圆内接正六边形的周长 , 则 . 再利用圆的内接正十二边形来计算圆周率则圆周率约为( )
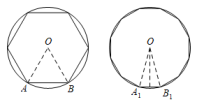 A、 B、 C、 D、
A、 B、 C、 D、
二、填空题(每题4分,共24分)
-
11. 已知圆的周长是 , 则该圆的内接正三角形的边心距是 .
-
12. 已知⊙O的直径AB长为2,弦AC长为 , 那么弦AC所对的圆周角的度数等于 .
-
13. 正六边形内接于 , , 则的半径是 .
-
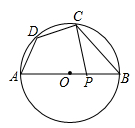
14. 如图,四边形ABCD内接于⊙O,AB为⊙O的直径,∠ADC=130°,连接AC,则∠BAC的度数为 .
-
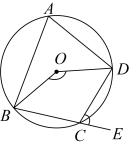
15. 如图,∠DCE是⊙O内接四边形ABCD的一个外角,若∠DCE=72°,那么∠BOD的度数为 .
-
16. 如图,正六边形和正五边形内接于 , 且有公共顶点A,则的度数为度.
三、解答题(共8题,共66分)
-
17. 已知四边形ABCD内接于⊙O,= , ∠ADC=120°,求证:△ABC是等边三角形.

-
18. 如图,四边形内接于 , , 求证: .

-
19. 如图,四边形ABCD是⊙O的内接四边形,连接AC,BD,延长CD至点E.
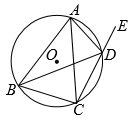 (1)、若AB=AC,求证:∠ADB=∠ADE;(2)、若BC=3,⊙O的半径为2,求sin∠BAC.
(1)、若AB=AC,求证:∠ADB=∠ADE;(2)、若BC=3,⊙O的半径为2,求sin∠BAC. -
20. 如图,为正五边形的外接圆,已知 , 请用无刻度直尺完成下列作图,保留必要的画图痕迹.
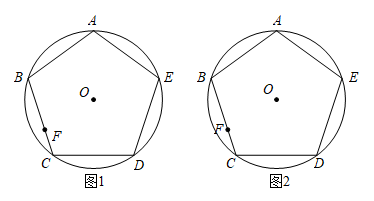 (1)、在图1中的边上求作点 , 使;(2)、在图2中的边上求作点 , 使 .
(1)、在图1中的边上求作点 , 使;(2)、在图2中的边上求作点 , 使 . -
21. 牂狗江“佘月郎山,西陵晚渡”的风景描绘中有半个月亮挂在山上,月亮之上有个“齐天大圣”守护洞口的传说.真实情况是老王山上有个月亮洞,洞顶上经常有猴子爬来爬去,下图是月亮洞的截面示意图.
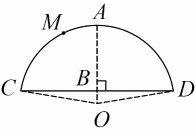 (1)、科考队测量出月亮洞的洞宽约是28m,洞高约是12m,通过计算截面所在圆的半径可以解释月亮洞像半个月亮,求半径的长(结果精确到0.1m);(2)、若 , 点在上,求的度数,并用数学知识解释为什么“齐天大圣”点在洞顶上巡视时总能看清洞口的情况.
(1)、科考队测量出月亮洞的洞宽约是28m,洞高约是12m,通过计算截面所在圆的半径可以解释月亮洞像半个月亮,求半径的长(结果精确到0.1m);(2)、若 , 点在上,求的度数,并用数学知识解释为什么“齐天大圣”点在洞顶上巡视时总能看清洞口的情况. -
22. 在半径为1的⊙O中,A、B、C、D中是圆上的四个点.
 (1)、如图1,若的度数为66°,的度数114°,求∠B的度数.(2)、如图2,若的度数为m°,的度数为n°,当m+n=180时,试求AB2+CD2的值.(3)、在(2)的条件下,若AB=a,BC=b,CD=c,DA=d,试求四边形ABCD的面积.(用含a,b,c,d的代数式表示)
(1)、如图1,若的度数为66°,的度数114°,求∠B的度数.(2)、如图2,若的度数为m°,的度数为n°,当m+n=180时,试求AB2+CD2的值.(3)、在(2)的条件下,若AB=a,BC=b,CD=c,DA=d,试求四边形ABCD的面积.(用含a,b,c,d的代数式表示) -
23. 如图,四边形ABCD内接于 , 对角线AC,BD相交于点E,点F在边AD上,连接EF.
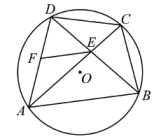 (1)、求证:;(2)、当时,则;;.(直接将结果填写在相应的横线上)(3)、①记四边形ABCD,的面积依次为 , 若满足 , 试判断,的形状,并说明理由.
(1)、求证:;(2)、当时,则;;.(直接将结果填写在相应的横线上)(3)、①记四边形ABCD,的面积依次为 , 若满足 , 试判断,的形状,并说明理由.②当 , 时,试用含m,n,p的式子表示.
-
24. 如图1,在矩形ABCD中,P是BC上的点,ΔABP沿AP折叠B点的对应点是M点,延长PM交直线AD于点E.
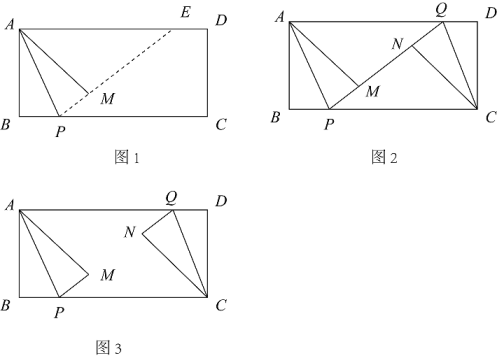 (1)、求证:EA=EP(2)、如图2,Q是AD上的点,QD=BP;ΔCDQ沿CQ折叠D点的对应点是N点,且P、M、N、Q在同一直线上.
(1)、求证:EA=EP(2)、如图2,Q是AD上的点,QD=BP;ΔCDQ沿CQ折叠D点的对应点是N点,且P、M、N、Q在同一直线上.①若AB=4,AD=8;求BP的长.
②若M、N互相重合;求的值;(自己画草图)
(3)、如图3,Q是AD上的点,QD=BP;ΔCDQ沿CQ折叠D点的对应点是N点,若AB=4,MN的最小值是1;求AD的长.
