浙教版备考2023年中考数学一轮复习71.三角形的内切圆与内心
试卷更新日期:2023-01-01 类型:一轮复习
一、单选题(每题3分,共30分)
-
1. 根据圆规作图的痕迹,可用直尺成功地找到三角形内心的是( )A、
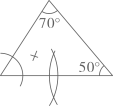 B、
B、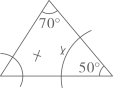 C、
C、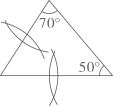 D、
D、 2. 如图,已知⊙O是△ABC的内切圆,且∠ABC=60°,∠ACB=80°,则∠BOC的度数为( )
2. 如图,已知⊙O是△ABC的内切圆,且∠ABC=60°,∠ACB=80°,则∠BOC的度数为( ) A、110° B、120° C、130° D、140°3. 如图,在正方形中,点E是对角线上一点(不与点B重合),若点O是的内心,则( )
A、110° B、120° C、130° D、140°3. 如图,在正方形中,点E是对角线上一点(不与点B重合),若点O是的内心,则( ) A、大小为定值,等于 B、大小不确定,可以等于 C、大小为定值,等于 D、大小不确定,随着点E的变化而变化4. 如图,⊙O是△ABC的内切圆,若∠A=70°,则∠BOC=( )
A、大小为定值,等于 B、大小不确定,可以等于 C、大小为定值,等于 D、大小不确定,随着点E的变化而变化4. 如图,⊙O是△ABC的内切圆,若∠A=70°,则∠BOC=( ) A、125° B、115° C、100° D、130°5. 在△ABC中,AC=BC=2 , AB=4,点O是△ABC的内心,则△ABC的内切圆半径为( )A、2 B、4﹣2 C、2﹣ D、2﹣26. 如图,BC是⊙O的直径,点A是⊙O上的一点,点D是△ABC的内心,若BC=5,AC=3,则BD的长度为( )
A、125° B、115° C、100° D、130°5. 在△ABC中,AC=BC=2 , AB=4,点O是△ABC的内心,则△ABC的内切圆半径为( )A、2 B、4﹣2 C、2﹣ D、2﹣26. 如图,BC是⊙O的直径,点A是⊙O上的一点,点D是△ABC的内心,若BC=5,AC=3,则BD的长度为( ) A、2 B、3 C、 D、7. 直角三角形的外接圆半径为3,内切圆半径为1,则该直角三角形的周长是( )A、12 B、14 C、16 D、188. 如图,等边内切的图形来自我国古代的太极图,等边三角形内切圆中的黑色部分和白色部分关于等边的内心成中心对称,则圆中的黑色部分的面积与的面积之比是( )
A、2 B、3 C、 D、7. 直角三角形的外接圆半径为3,内切圆半径为1,则该直角三角形的周长是( )A、12 B、14 C、16 D、188. 如图,等边内切的图形来自我国古代的太极图,等边三角形内切圆中的黑色部分和白色部分关于等边的内心成中心对称,则圆中的黑色部分的面积与的面积之比是( ) A、 B、 C、 D、9. 如图,在Rt△ABC中,∠C=90°,AC=5,⊙O是△ABC的内切圆,半径为2,则图中阴影部分的面积为( )
A、 B、 C、 D、9. 如图,在Rt△ABC中,∠C=90°,AC=5,⊙O是△ABC的内切圆,半径为2,则图中阴影部分的面积为( ) A、30﹣4π B、 C、60﹣16π D、10. 如图,已知 , 用尺规按照下面步骤操作:
A、30﹣4π B、 C、60﹣16π D、10. 如图,已知 , 用尺规按照下面步骤操作:①作线段的垂直平分线;②作线段的垂直平分线 , 交于点O;③以O为圆心,长为半径作 .
结论Ⅰ:点O是的内心.
结论Ⅱ: .
对于结论Ⅰ和结论Ⅱ,下列判断正确的是( )
 A、Ⅰ和Ⅱ都对 B、Ⅰ和Ⅱ都不对 C、Ⅰ不对Ⅱ对 D、Ⅰ对Ⅱ不对
A、Ⅰ和Ⅱ都对 B、Ⅰ和Ⅱ都不对 C、Ⅰ不对Ⅱ对 D、Ⅰ对Ⅱ不对二、填空题(每题4分,共24分)
-
11. 我国古代数学家赵爽的“弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形(如图所示).若直角三角形的内切圆半径为3,小正方形的面积为49,则大正方形的面积为.
 12. 如图,直线 , , 与分别相切于点D,E,F,若 , , , 则 . (用含、的式子表示)
12. 如图,直线 , , 与分别相切于点D,E,F,若 , , , 则 . (用含、的式子表示) 13. 已知△ABC为直角三角形,它的内切圆的半径为2cm,两直角边的长分别是关于x的方程x2﹣17x+6m=0的两个根,则△ABC的面积为(cm2).14. 如图,大圆和小圆是等边三角形的外接圆和内切圆,现随机向该图形内掷一枚小针,则针尖落在小圆区域的概率为 .
13. 已知△ABC为直角三角形,它的内切圆的半径为2cm,两直角边的长分别是关于x的方程x2﹣17x+6m=0的两个根,则△ABC的面积为(cm2).14. 如图,大圆和小圆是等边三角形的外接圆和内切圆,现随机向该图形内掷一枚小针,则针尖落在小圆区域的概率为 .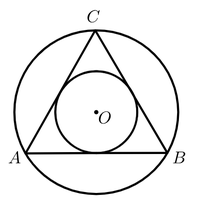 15. 如图上,O为内心,过点O的直线分别与AC、AB相交于D、E,若DE=CD+BE,则线段CD的长为.
15. 如图上,O为内心,过点O的直线分别与AC、AB相交于D、E,若DE=CD+BE,则线段CD的长为.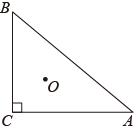 16. 如图, 和 均是等边三角形,其中点 是 的内心,以 为圆心, 长为半径画弧交 于点 ,再将弧 绕点 逆时针旋转60°至弧 处,已知 ,则图中阴影部分面积是 .
16. 如图, 和 均是等边三角形,其中点 是 的内心,以 为圆心, 长为半径画弧交 于点 ,再将弧 绕点 逆时针旋转60°至弧 处,已知 ,则图中阴影部分面积是 .
三、作图题(共8分)
-
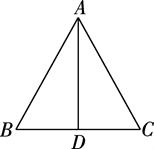
17. 如图,在 中, ,AD为底边BC上的高,请用尺规作图法,作 的内切圆⊙O.(保留作图痕迹,不写作法)
四、解答题(共6题,共58分)
-
18. 如图:在三角形ABC中,AB=5,AC=7,BC=8,求其内切圆的半径.
 19. 如图, 是 的外接圆,点E是 的内心,AE的延长线交BC于点F,交 于点D,连接BD,BE.
19. 如图, 是 的外接圆,点E是 的内心,AE的延长线交BC于点F,交 于点D,连接BD,BE. (1)、求证: ;(2)、若 , ,求DB的长.20. 如图,四边形ABCD是⊙O的内接四边形,对角线AC是⊙O的直径,AB=2,I是△ADC的内心,∠ADB=45°.
(1)、求证: ;(2)、若 , ,求DB的长.20. 如图,四边形ABCD是⊙O的内接四边形,对角线AC是⊙O的直径,AB=2,I是△ADC的内心,∠ADB=45°.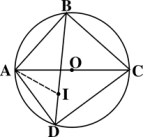 (1)、求⊙O半径的长;(2)、求证:BC=BI.21. 如图,中, , 是的内切圆,D,E,F是切点.
(1)、求⊙O半径的长;(2)、求证:BC=BI.21. 如图,中, , 是的内切圆,D,E,F是切点.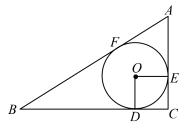 (1)、求证:四边形ODCE是正方形;(2)、如果 , , 求内切圆的半径.
(1)、求证:四边形ODCE是正方形;(2)、如果 , , 求内切圆的半径.
-

