浙教版备考2023年中考数学一轮复习70.三角形的外接圆与外心
试卷更新日期:2023-01-01 类型:一轮复习
一、单选题(每题3分,共30分)
-
1. 的外心在三角形的内部,则是( )A、锐角三角形 B、直角三角形 C、钝角三角形 D、无法判断2. 直角三角形的外心在( )A、直角顶点 B、直角三角形内 C、直角三角形外 D、斜边中点3. 三角形的外心是三角形的( )A、三条中线的交点 B、三条角平分线的交点 C、三边垂直平分线的交点 D、三条高所在直线的交点4. 如图,已知点A(3,6)、B(1,4)、C(1,0),则△ABC外接圆的圆心坐标是( )
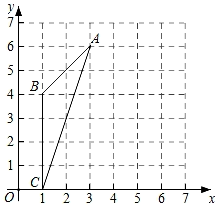 A、(0,0) B、(2,3) C、(5,2) D、(1,4)5. 如图,点O是△ABC的外心(三角形三边垂直平分线的交点),若∠BOC=96°,则∠A的度数为( )
A、(0,0) B、(2,3) C、(5,2) D、(1,4)5. 如图,点O是△ABC的外心(三角形三边垂直平分线的交点),若∠BOC=96°,则∠A的度数为( )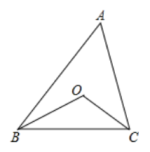 A、49° B、47.5° C、48° D、不能确定6. 如图在△ABC中,边AB,AC的垂直平分线交于点P,连结BP,CP,若∠A=50°,则∠BPC=( )
A、49° B、47.5° C、48° D、不能确定6. 如图在△ABC中,边AB,AC的垂直平分线交于点P,连结BP,CP,若∠A=50°,则∠BPC=( )
 A、100° B、95° C、90° D、50°7. 若AM、AN分别是的高线和中线,AG是的角平分线,则( )A、 B、 C、 D、8. 如图,已知△ABC内接于半径为1的⊙O,∠BAC=θ(θ是锐角),则△ABC的面积的最大值为( )
A、100° B、95° C、90° D、50°7. 若AM、AN分别是的高线和中线,AG是的角平分线,则( )A、 B、 C、 D、8. 如图,已知△ABC内接于半径为1的⊙O,∠BAC=θ(θ是锐角),则△ABC的面积的最大值为( )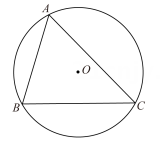 A、cosθ(1+cosθ) B、cosθ(1+sinθ) C、sinθ(1+sinθ) D、sinθ(1+cosθ)9. 如图,O为锐角三角形ABC的外心,四边形OCDE为正方形,其中E点在△ABC的外部,判断下列叙述不正确的是( )
A、cosθ(1+cosθ) B、cosθ(1+sinθ) C、sinθ(1+sinθ) D、sinθ(1+cosθ)9. 如图,O为锐角三角形ABC的外心,四边形OCDE为正方形,其中E点在△ABC的外部,判断下列叙述不正确的是( )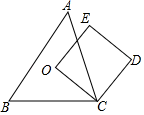 A、O是△AEB的外心,O不是△AED的外心 B、O是△BEC的外心,O不是△BCD的外心 C、O是△AEC的外心,O不是△BCD的外心 D、O是△ADB的外心,O不是△ADC的外心10. 如图,点 是 的内心, 的延长线和 的外接圆相交于点 ,与 相交于点 ,则下列结论:① ;②若 ,则 ;③若点 为 的中点,则 ;④ .其中一定正确的个数是( )
A、O是△AEB的外心,O不是△AED的外心 B、O是△BEC的外心,O不是△BCD的外心 C、O是△AEC的外心,O不是△BCD的外心 D、O是△ADB的外心,O不是△ADC的外心10. 如图,点 是 的内心, 的延长线和 的外接圆相交于点 ,与 相交于点 ,则下列结论:① ;②若 ,则 ;③若点 为 的中点,则 ;④ .其中一定正确的个数是( )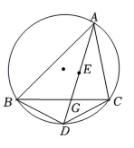 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题(每题4分,共24分)
-
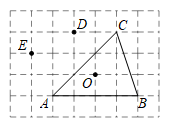
11. 如图,在 网格中,各小正方形边长均为1,点O,A,B,C,D,E均在格点上,点O是 的外心,在不添加其他字母的情况下,则除 外把你认为外心也是O的三角形都写出来 .
 12. 如图所示的网格由边长均为1的小正方形组成,点A、B、C、D、E、F在小正方形的顶点上,则外接圆的圆心是点 , 弧的长是.
12. 如图所示的网格由边长均为1的小正方形组成,点A、B、C、D、E、F在小正方形的顶点上,则外接圆的圆心是点 , 弧的长是.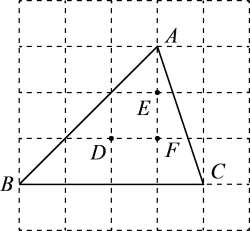 13. 在 中,若 , ,则 的面积的最大值为.14. 已知 的三边 、 、 满足 ,则 的外接圆半径.15. 已知一个直角三角形的两边长分别为5cm,12cm,则此三角形的外接圆半径是 .16. 如图,点I和O分别是△ABC的内心和外心,若∠AIB=125°,则∠AOB的度数为 .
13. 在 中,若 , ,则 的面积的最大值为.14. 已知 的三边 、 、 满足 ,则 的外接圆半径.15. 已知一个直角三角形的两边长分别为5cm,12cm,则此三角形的外接圆半径是 .16. 如图,点I和O分别是△ABC的内心和外心,若∠AIB=125°,则∠AOB的度数为 .
三、解答题(共8题,共66分)
-
17. 如图, 的半径为R,其内接锐角三角形ABC中, 、 、 所对的边分别是a、b、c
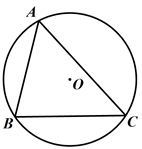 (1)、求证:(2)、若 , , ,利用(1)的结论求AB的长和 的值18. 如图,在△ABC中,AD是边BC上的中线,∠BAD=∠CAD,CE∥AD,CE交BA的延长线于点E,BC=8,AD=3.
(1)、求证:(2)、若 , , ,利用(1)的结论求AB的长和 的值18. 如图,在△ABC中,AD是边BC上的中线,∠BAD=∠CAD,CE∥AD,CE交BA的延长线于点E,BC=8,AD=3.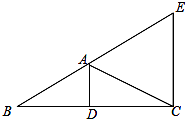 (1)、求CE的长;(2)、求证:△ABC为等腰三角形.(3)、求△ABC的外接圆圆心P与内切圆圆心Q之间的距离.19.(1)、请在图中作出的外接圆(尺规作图,保留作图痕迹,不写作法);
(1)、求CE的长;(2)、求证:△ABC为等腰三角形.(3)、求△ABC的外接圆圆心P与内切圆圆心Q之间的距离.19.(1)、请在图中作出的外接圆(尺规作图,保留作图痕迹,不写作法);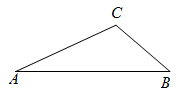 (2)、如图,是的外接圆,是的直径,点是的中点,过点的切线与的延长线交于点.
(2)、如图,是的外接圆,是的直径,点是的中点,过点的切线与的延长线交于点.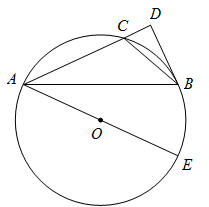
①求证:;
②若 , , 求的半径.
20. 如图,正三角形、正方形、正六边形等正n边形与圆的形状有差异,我们将正n边形与圆的接近程度称为“接近度”.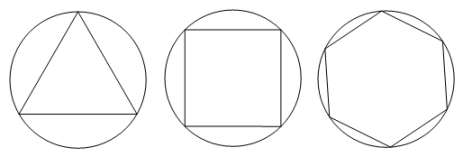 (1)、角的“接近度”定义:设正n边形的每个内角的度数为 , 将正n边形的“接近度”定义为.于是越小,该正n边形就越接近于圆,
(1)、角的“接近度”定义:设正n边形的每个内角的度数为 , 将正n边形的“接近度”定义为.于是越小,该正n边形就越接近于圆,①若 , 则该正n边形的“接近度”等于.
②若 , 则该正n边形的“接近度”等于.
③当“接近度”等于.时,正n边形就成了圆.
(2)、边的“接近度”定义:设一个正n边形的外接圆的半径为R,正n边形的中心到各边的距离为d,将正n边形的“接近度”定义为.分别计算时边的“接近度”,并猜测当边的“接近度”等于多少时,正n边形就成了圆?21. 在学习三角形高线时,发现三角形三条高线交于一点,我们把这个交点叫做三角形的垂心.课后小明同学继续探究,上网搜索得到了三角形重心的一条性质,制作了如下表格进行探究.三角形关型
直角三角形
锐角三角形
钝角三角形
垂心的位置
直角顶点
①
在三角形外部
垂心的性质
三角形任意顶点到垂心的距离等于外心到对边的距离的两倍.
图形
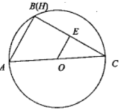 图1
图1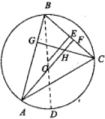 图2(1)、表格中①处应填:.(2)、小明先选择了直角三角形来探究重心的性质,写出了已知求证,请完成证明.
图2(1)、表格中①处应填:.(2)、小明先选择了直角三角形来探究重心的性质,写出了已知求证,请完成证明.已知:如图1,⊙O是的外接圆, , H是的垂心, , 垂足为E.
求证:.
(3)、如图2,⊙O是锐角三角形ABC的外接圆,高线AF与高线CG交于点H,于点E,为了证明.小明想把锐角三角形的问题转化为直角三角形,为此他过点B作了⊙O的直径BD,请继续小明的思路证明.22. 阅读下列材料:已知实数m,n满足(2m2+n2+1)(2m2+n2-1)=80,试求2m2+n2的值.
解:设2m2+n2=t,则原方程变为(t+1)(t-1)=80,整理得t2-1=80,t2=81,
所以t=±9,因为2m2+n2≥0,所以2m2+n2=9.
上面这种方法称为“换元法”,把其中某些部分看成一个整体,并用新字母代替(即换元),则能使复杂的问题简单化.
根据以上阅读材料内容,解决下列问题,并写出解答过程.
(1)、已知实数x、y,满足(2x2+2y2+3)(2x2+2y2-3)=27,求x2+y2的值;(2)、已知Rt△ACB的三边为a、b、c(c为斜边),其中a、b满足(a2+b2)(a2+b2-4)=5,求Rt△ACB外接圆的半径.23. 如图,AD是△ABC的外角∠EAC的平分线,与△ABC的外接圆⊙O交于点D,∠EAC=120°.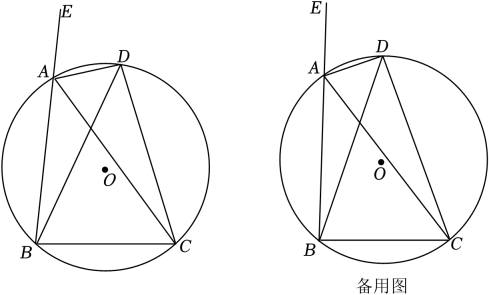 (1)、求的度数;(2)、连DB,DC,求证:DB=DC;(3)、探究线段AD,AB,AC之间的数量关系,并证明你的结论.24.
(1)、求的度数;(2)、连DB,DC,求证:DB=DC;(3)、探究线段AD,AB,AC之间的数量关系,并证明你的结论.24.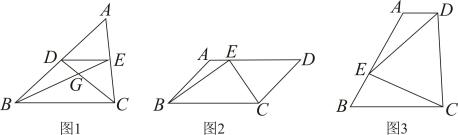 (1)、问题提出:如图1,在中,点、分别是、的中点,连接、、 , 与交于点 , 若 , 则;(2)、问题探究:如图2,在中, , , 点是上一点(可与端点重合),连接、 , , 求面积的最小值;(3)、问题解决:某湿地公园拟建一个梯形花园 , 示意图如图3所示,其中 , , .管理员计划在区域种植水生植物,在区域种植甲种花卉.根据设计要求,要满足点在上, , 是锐角,且 , 若种植水生植物每平方米需400元,种植甲种花卉每平方米需100元,求种植水生植物和种植甲种花卉所需总费用至少为多少元?
(1)、问题提出:如图1,在中,点、分别是、的中点,连接、、 , 与交于点 , 若 , 则;(2)、问题探究:如图2,在中, , , 点是上一点(可与端点重合),连接、 , , 求面积的最小值;(3)、问题解决:某湿地公园拟建一个梯形花园 , 示意图如图3所示,其中 , , .管理员计划在区域种植水生植物,在区域种植甲种花卉.根据设计要求,要满足点在上, , 是锐角,且 , 若种植水生植物每平方米需400元,种植甲种花卉每平方米需100元,求种植水生植物和种植甲种花卉所需总费用至少为多少元?