浙教版备考2023年中考数学一轮复习69.圆与圆的位置关系
试卷更新日期:2023-01-01 类型:一轮复习
一、单选题(每题3分,共30分)
-
1. ⊙O1和⊙O2的半径分别为5和2,O1O2=3,则⊙O1和⊙O2的位置关系是( )A、内含 B、 内切 C、相交 D、外切2. 已知圆、圆的半径不相等,圆的半径长为5,若圆上的点A满足 , 则圆与圆的位置关系是( )A、相交或相切 B、相切或相离 C、相交或内含 D、相切或内含3. 如图,在矩形ABCD中,点E是CD的中点,联结BE,如果AB=6,BC=4,那么分别以AD、BE为直径的⊙M与⊙N的位置关系是( )
 A、外离 B、外切 C、相交 D、内切4. 已知两圆相交,当每个圆的圆心都在在另一个圆的圆外时,我们称此两圆的位置关系为“外相交”.已知两圆“外相交”,且半径分别为2和5,则圆心距的取值可以是()A、4 B、5 C、6 D、75. 实验学校的花坛形状如图所示,其中,等圆⊙O1与⊙O2的半径为3米,且⊙O1经过⊙O2的圆心O2 . 已知实线部分为此花坛的周长,则花坛的周长为( )
A、外离 B、外切 C、相交 D、内切4. 已知两圆相交,当每个圆的圆心都在在另一个圆的圆外时,我们称此两圆的位置关系为“外相交”.已知两圆“外相交”,且半径分别为2和5,则圆心距的取值可以是()A、4 B、5 C、6 D、75. 实验学校的花坛形状如图所示,其中,等圆⊙O1与⊙O2的半径为3米,且⊙O1经过⊙O2的圆心O2 . 已知实线部分为此花坛的周长,则花坛的周长为( ) A、4π米 B、6π米 C、8π米 D、12π米6. 如图,在Rt△ABC中,∠C=90°,AC=8,BC=6,两等圆⊙A,⊙B外切,图中阴影部分面积为( )
A、4π米 B、6π米 C、8π米 D、12π米6. 如图,在Rt△ABC中,∠C=90°,AC=8,BC=6,两等圆⊙A,⊙B外切,图中阴影部分面积为( ) A、 B、 C、 D、7. 如图,两个等圆⊙O1和⊙O2相交于A、B两点,且⊙O1经过⊙O2的圆心,则∠O1AB的度数为( )
A、 B、 C、 D、7. 如图,两个等圆⊙O1和⊙O2相交于A、B两点,且⊙O1经过⊙O2的圆心,则∠O1AB的度数为( ) A、45° B、30° C、20° D、15°8. 已知直径分别为6和10的两圆没有公共点,那么这两个圆的圆心距的取值范围是( )A、d>2 B、d>8 C、d>8或0≤d<2 D、2≤d<89. 如图,⊙O的半径是4,A为⊙O上一点,M是⊙A上一点(M在⊙O内),过点M作⊙A切线l,且l与⊙O相交于P,Q两点,若⊙A的半径为2,当线段PQ最长时线段OM的长度为m,当线段PQ最短时线段OM的长度为n,则m﹣n的值是( )
A、45° B、30° C、20° D、15°8. 已知直径分别为6和10的两圆没有公共点,那么这两个圆的圆心距的取值范围是( )A、d>2 B、d>8 C、d>8或0≤d<2 D、2≤d<89. 如图,⊙O的半径是4,A为⊙O上一点,M是⊙A上一点(M在⊙O内),过点M作⊙A切线l,且l与⊙O相交于P,Q两点,若⊙A的半径为2,当线段PQ最长时线段OM的长度为m,当线段PQ最短时线段OM的长度为n,则m﹣n的值是( )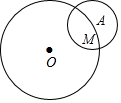 A、2﹣3 B、 C、2﹣2 D、2﹣210. 如图,在 中, , , ,点P在边 上, 的半径为3, 的半径为2,如果 和 相交,那么线段 长的取值范围是( )
A、2﹣3 B、 C、2﹣2 D、2﹣210. 如图,在 中, , , ,点P在边 上, 的半径为3, 的半径为2,如果 和 相交,那么线段 长的取值范围是( )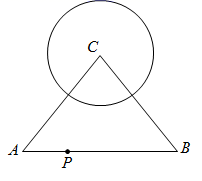 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每空3分,共18分)
-
11. 若两个圆的半径分别为3和4,圆心之间的距离是5,则这两个圆的位置关系是 .12. 已知⊙O1的半径为3,⊙O2的半径为r,⊙O1与⊙O2只能画出两条不同的公共切线,且O1O2=5,则⊙O2的半径为r的取值范围是 .
13. 已知两圆的半径长分别为2和5,两圆的圆心距为d,如果两圆没有公共点,那么d的取值范围是14. 已知⊙与⊙的半径分别是方程的两根,且 , 若这两个圆相切,则= .15. 如图,在直角梯形中, , , 是上一定点, , , , , 点是上一个动点,以为圆心,为半径作 , 若与以为圆心,1为半径的有公共点,且与线段只有一个交点,则长度的取值范围是 . 16. 如图,半径均为4的⊙O1、⊙O2、⊙O3两两外切,点O1、O2、O3分别为圆心,则图中阴影部分的面积为 .
16. 如图,半径均为4的⊙O1、⊙O2、⊙O3两两外切,点O1、O2、O3分别为圆心,则图中阴影部分的面积为 .
三、解答题(共9题,共72分)
-
17. 已知:如图,⊙O1与⊙O2相交于A、B,若两圆半径分别为17cm和10cm,公共弦AB=16cm,求O1O2的长.
 18. 如图,在Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm.P为BC的中点,动点Q从点P出发,沿射线PC方向以2cm/s的速度运动,以P为圆心,PQ长为半径作圆.设点Q运动的时间为t s.
18. 如图,在Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm.P为BC的中点,动点Q从点P出发,沿射线PC方向以2cm/s的速度运动,以P为圆心,PQ长为半径作圆.设点Q运动的时间为t s.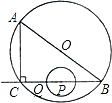 (1)、当t=1.2时,判断直线AB与⊙P的位置关系,并说明理由;(2)、已知⊙O为△ABC的外接圆.若⊙P与⊙O相切,求t的值.19. 如图,在平面直角坐标系中,⊙C与y轴相切,且点C坐标为(1,0),直线l过点A(-1,0),与⊙C相切于点D.
(1)、当t=1.2时,判断直线AB与⊙P的位置关系,并说明理由;(2)、已知⊙O为△ABC的外接圆.若⊙P与⊙O相切,求t的值.19. 如图,在平面直角坐标系中,⊙C与y轴相切,且点C坐标为(1,0),直线l过点A(-1,0),与⊙C相切于点D.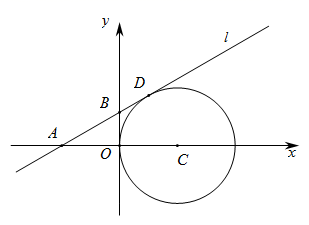 (1)、求直线l的解析式.(2)、是否存在⊙P,使圆心P在x轴上,且与直线l相切,与⊙C外切?如果存在,请直接写出圆心P的坐标;如果不存在,请说明理由.20. 阅读理解,我们已经学习了点和圆、直线和圆的位置关系以及各种位置关系的数量表示,如下表:
(1)、求直线l的解析式.(2)、是否存在⊙P,使圆心P在x轴上,且与直线l相切,与⊙C外切?如果存在,请直接写出圆心P的坐标;如果不存在,请说明理由.20. 阅读理解,我们已经学习了点和圆、直线和圆的位置关系以及各种位置关系的数量表示,如下表:
类似于研究点和圆、直线和圆的位置关系,我们也可以用两圆的半径和两圆的圆心距(两圆圆心的距离)来刻画两圆的位置关系.如果两圆的半径分别为 和 (r1>r2),圆心距为d,请你通过画图,并利用d与 和 之间的数量关系探索两圆的位置关系.
图形表示
(圆和圆的位置关系)
数量表示
(圆心距d与两圆的半径 、 的数量关系)
21. 如图,在平面直角坐标系 中,抛物线 与x轴相交于点 , ,与y轴交于点C.将抛物线的对称轴沿x轴的正方向平移,平移后交x轴于点D , 交线段 于点E , 交抛物线于点F , 过点F作直线 的垂线,垂足为点G. (1)、求抛物线的表达式;(2)、以点G为圆心, 为半径画 ;以点E为圆心, 为半径画 .当 与 内切时.
(1)、求抛物线的表达式;(2)、以点G为圆心, 为半径画 ;以点E为圆心, 为半径画 .当 与 内切时.①试证明 与 的数量关系;
②求点F的坐标.
22. 已知圆O的半径长为2,点A、B、C为圆O上三点,弦 , 点D为BC的中点, (1)、如图,连接AC、OD,设 , 请用α表示;(2)、如图,当点B为的中点时,求点A、D之间的距离.(3)、如果AD的延长线与圆O交于点E,以O为圆心,AD为半径的圆与以BC为直径的圆有且只有一个交点,求弦AE的长.23. 如图,已知扇形AOB的半径OA=4,∠AOB=90°,点C、D分别在半径OA、OB上(点C不与点A重合),联结CD . 点P是弧AB上一点,PC=PD .
(1)、如图,连接AC、OD,设 , 请用α表示;(2)、如图,当点B为的中点时,求点A、D之间的距离.(3)、如果AD的延长线与圆O交于点E,以O为圆心,AD为半径的圆与以BC为直径的圆有且只有一个交点,求弦AE的长.23. 如图,已知扇形AOB的半径OA=4,∠AOB=90°,点C、D分别在半径OA、OB上(点C不与点A重合),联结CD . 点P是弧AB上一点,PC=PD . (1)、当cot∠ODC= ,以CD为半径的圆D与圆O相切时,求CD的长;(2)、当点D与点B重合,点P为弧AB的中点时,求∠OCD的度数;(3)、如果OC=2,且四边形ODPC是梯形,求 的值.24. 梯形中, , 于点 , , , 以为直径,以为直径,直线与交于点 , 与交于点(如图),设 .
(1)、当cot∠ODC= ,以CD为半径的圆D与圆O相切时,求CD的长;(2)、当点D与点B重合,点P为弧AB的中点时,求∠OCD的度数;(3)、如果OC=2,且四边形ODPC是梯形,求 的值.24. 梯形中, , 于点 , , , 以为直径,以为直径,直线与交于点 , 与交于点(如图),设 .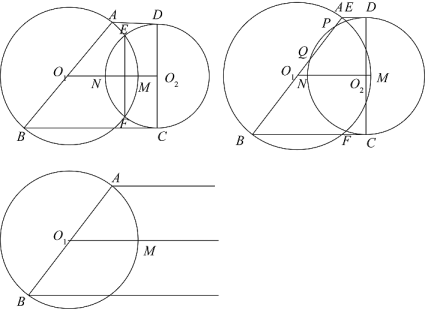 (1)、记两圆交点为、(在上方),当时,求的值;(2)、当与线段交于、时,设 , 求关于的函数关系式,并写出定义域;(3)、连接 , 线段与交于点 , 分别连接、 , 若与相似,求的值.25. 在梯形ABCD中,AD∥BC , AB⊥BC , AD=3,CD=5,cosC= (如图).M是边BC上一个动点(不与点B、C重合),以点M为圆心,CM为半径作圆,⊙M与射线CD、射线MA分别相交于点E、F .
(1)、记两圆交点为、(在上方),当时,求的值;(2)、当与线段交于、时,设 , 求关于的函数关系式,并写出定义域;(3)、连接 , 线段与交于点 , 分别连接、 , 若与相似,求的值.25. 在梯形ABCD中,AD∥BC , AB⊥BC , AD=3,CD=5,cosC= (如图).M是边BC上一个动点(不与点B、C重合),以点M为圆心,CM为半径作圆,⊙M与射线CD、射线MA分别相交于点E、F . (1)、设CE= ,求证:四边形AMCD是平行四边形;(2)、联结EM , 设∠FMB=∠EMC , 求CE的长;(3)、以点D为圆心,DA为半径作圆,⊙D与⊙M的公共弦恰好经过梯形的一个顶点,求此时⊙M的半径长.
(1)、设CE= ,求证:四边形AMCD是平行四边形;(2)、联结EM , 设∠FMB=∠EMC , 求CE的长;(3)、以点D为圆心,DA为半径作圆,⊙D与⊙M的公共弦恰好经过梯形的一个顶点,求此时⊙M的半径长.