浙教版备考2023年中考数学一轮复习68.切线的性质与判定
试卷更新日期:2023-01-01 类型:一轮复习
一、单选题(每题3分,共30分)
-
1. 如图是“光盘行动”的宣传海报,图中餐盘与筷子可看成直线和圆的位置关系是( )
 A、相切 B、相交 C、相离 D、平行2. 如图,、分别与相切于点、 , 连接并延长与交于点、 , 若 , , 则的值为( )
A、相切 B、相交 C、相离 D、平行2. 如图,、分别与相切于点、 , 连接并延长与交于点、 , 若 , , 则的值为( ) A、 B、 C、 D、3. 如图,是的直径,点P在的延长线上,与相切于点A,连接 , 若 , 则的度数为( )
A、 B、 C、 D、3. 如图,是的直径,点P在的延长线上,与相切于点A,连接 , 若 , 则的度数为( ) A、 B、 C、 D、4. 为⊙ 外一点, 与⊙ 相切于点 , , ,则 的长为( )A、 B、5 C、8 D、95. 如图,为的直径,过点A作的切线交的延长线于点C,连接 , , 若 , 则( )
A、 B、 C、 D、4. 为⊙ 外一点, 与⊙ 相切于点 , , ,则 的长为( )A、 B、5 C、8 D、95. 如图,为的直径,过点A作的切线交的延长线于点C,连接 , , 若 , 则( ) A、 B、 C、 D、6. 如图,AB、AC、BD是⊙O的切线,切点分别为P、C、D,若 , , 则BD的长是( )
A、 B、 C、 D、6. 如图,AB、AC、BD是⊙O的切线,切点分别为P、C、D,若 , , 则BD的长是( ) A、2.5 B、2 C、1.5 D、17. 把量角器和含角的三角板按如图方式摆放:零刻度线与长直角边重合,移动量角器使外圆弧与斜边相切时,发现中心恰好在刻度处,短直角边过量角器外沿刻度处(即 , ).则阴影部分的面积为( )
A、2.5 B、2 C、1.5 D、17. 把量角器和含角的三角板按如图方式摆放:零刻度线与长直角边重合,移动量角器使外圆弧与斜边相切时,发现中心恰好在刻度处,短直角边过量角器外沿刻度处(即 , ).则阴影部分的面积为( )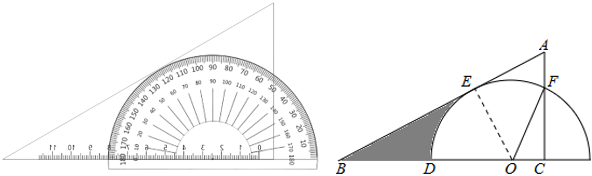 A、 B、 C、 D、8. 如图,以正方形的边为直径作半圆O过点C作直线切半圆于点F,交边于点E,若的周长为12,则线段的长为( )
A、 B、 C、 D、8. 如图,以正方形的边为直径作半圆O过点C作直线切半圆于点F,交边于点E,若的周长为12,则线段的长为( ) A、1 B、2 C、 D、9. 如图,中, , O是AB边上一点,与AC、BC都相切,若 , , 则的半径为( )
A、1 B、2 C、 D、9. 如图,中, , O是AB边上一点,与AC、BC都相切,若 , , 则的半径为( )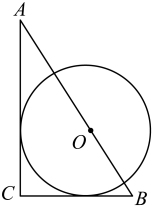 A、1 B、2 C、 D、10. 如图,的内切圆⊙O与BC,CA,AB分别相切于点D,E,F,已知的周长为36. , , 则AF的长为( )
A、1 B、2 C、 D、10. 如图,的内切圆⊙O与BC,CA,AB分别相切于点D,E,F,已知的周长为36. , , 则AF的长为( ) A、4 B、5 C、9 D、13
A、4 B、5 C、9 D、13二、填空题(每题4分,共24分)
-
11. 在矩形ABCD中,AB=6,BC=8,点O在对角线AC上,圆O的半径为2,如果圆O与矩形ABCD的各边都没有公共点,那么线段AO长的取值范围是 .12. 如图,在中, , , , 半径为1的在内平移(可以与该三角形的边相切),则点到上的点的距离的最大值为.
 13. 如图,PA,PB是⊙O的切线,A,B为切点,∠OAB=38°,则∠P=°.
13. 如图,PA,PB是⊙O的切线,A,B为切点,∠OAB=38°,则∠P=°.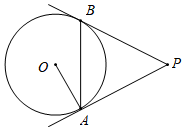 14. 如图,线段AB经过圆心O,交⊙O于点A、C,∠B=30°,直线BD与⊙O切于点D,则∠ADB的度数是 .
14. 如图,线段AB经过圆心O,交⊙O于点A、C,∠B=30°,直线BD与⊙O切于点D,则∠ADB的度数是 .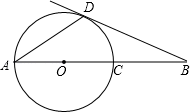 15. 如图, , 分别与相切于点 , ,直线与相切于点 , 分别交 , 于 , , 且 , 则的周长为 .
15. 如图, , 分别与相切于点 , ,直线与相切于点 , 分别交 , 于 , , 且 , 则的周长为 . 16. 如图,在正六边形内取一点 , 作与边相切,并经过点 , 已知的半经为 , 则正六边形的边长为.
16. 如图,在正六边形内取一点 , 作与边相切,并经过点 , 已知的半经为 , 则正六边形的边长为.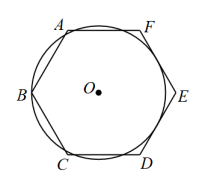
三、作图题(共10分)
-
17. 如图,已知点M在直线l外,点N在直线l上,请用无刻度的直尺和圆规完成下列作图,要求保留痕迹,不写作法.
 (1)、在图①中,以线段MN为一条对角线作菱形MPNQ,使菱形的边PN落在直线l上(2)、在图②中,做圆O,使圆O过点M,且与直线l相切于N.
(1)、在图①中,以线段MN为一条对角线作菱形MPNQ,使菱形的边PN落在直线l上(2)、在图②中,做圆O,使圆O过点M,且与直线l相切于N.四、解答题(共7题,共56分)
-
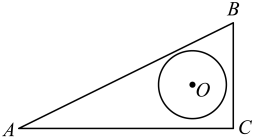
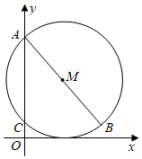
18. 如图,在平面直角坐标系中,以点M(3,5)为圆心,AB为直径的圆与x轴相切,与y轴交于A,C两点,求点B的坐标.
 19. 如图,是的内接三角形, , 经过圆心交于点 , 连接 , .
19. 如图,是的内接三角形, , 经过圆心交于点 , 连接 , . (1)、判断直线与的位置关系,并说明理由;(2)、若 , 求图中阴影部分的面积.20. 如图,AB是半圆O的直径,点C在半圆O上,点D为的中点,连接AC,BC,AD,AD与BC相交于点G,过点D作直线DEBC,交AC的延长线于点E.
(1)、判断直线与的位置关系,并说明理由;(2)、若 , 求图中阴影部分的面积.20. 如图,AB是半圆O的直径,点C在半圆O上,点D为的中点,连接AC,BC,AD,AD与BC相交于点G,过点D作直线DEBC,交AC的延长线于点E.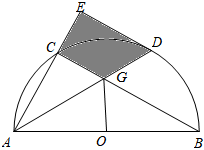 (1)、求证:DE是⊙O的切线;(2)、若 , CG=2 , 求阴影部分的面积.21. 如图,AB是⊙O的直径,点E在⊙O上,连接AE和BE,BC平分∠ABE交⊙O于点C,过点C作CD⊥BE,交BE的延长线于点D,连接CE.
(1)、求证:DE是⊙O的切线;(2)、若 , CG=2 , 求阴影部分的面积.21. 如图,AB是⊙O的直径,点E在⊙O上,连接AE和BE,BC平分∠ABE交⊙O于点C,过点C作CD⊥BE,交BE的延长线于点D,连接CE.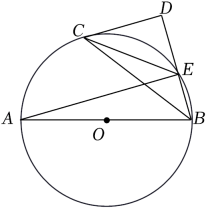 (1)、请判断直线CD与⊙O的位置关系,并说明理由;(2)、若sin∠ECD= , CE=5,求⊙O的半径.22. 如图,是的直径,P为半圆的中点,连接并延长至点B,使 , 连接 .
(1)、请判断直线CD与⊙O的位置关系,并说明理由;(2)、若sin∠ECD= , CE=5,求⊙O的半径.22. 如图,是的直径,P为半圆的中点,连接并延长至点B,使 , 连接 .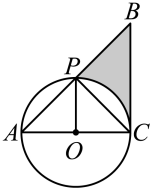 (1)、求证:为的切线;(2)、若 , 求图中阴影部分的面积.23. 我们学习过利用尺规作图平分一个任意角,而“利用尺规作图三等分一个任意角”曾是数学史上一大难题,之后被数学家证明是不可能完成的.人们根据实际需要,发明了一种简易操作工具—“三分角器”.图1是它的示意图,其中如与半圆O的直径BC在同一直线上,且AB的长度与半圆的半径相等;DB与AC垂直于点B,DB足够长.使用方法如图2所示,若要把∠MEN三等分,只需适当放置三分角器,使DB经过∠MEN的顶点E,点A落在边EM上,半圆O与另一边EN恰好相切,切点为F,则EB,EO就把∠MEN三等分了.为了说明这一方法的正确性,需要对其进行证明.如下给出了不完整的“已知”和“求证”,请补充完整,并写出“证明”过程.
(1)、求证:为的切线;(2)、若 , 求图中阴影部分的面积.23. 我们学习过利用尺规作图平分一个任意角,而“利用尺规作图三等分一个任意角”曾是数学史上一大难题,之后被数学家证明是不可能完成的.人们根据实际需要,发明了一种简易操作工具—“三分角器”.图1是它的示意图,其中如与半圆O的直径BC在同一直线上,且AB的长度与半圆的半径相等;DB与AC垂直于点B,DB足够长.使用方法如图2所示,若要把∠MEN三等分,只需适当放置三分角器,使DB经过∠MEN的顶点E,点A落在边EM上,半圆O与另一边EN恰好相切,切点为F,则EB,EO就把∠MEN三等分了.为了说明这一方法的正确性,需要对其进行证明.如下给出了不完整的“已知”和“求证”,请补充完整,并写出“证明”过程.已知:如图2,点A,B,O,C在同一直线上, , 垂足为点B,半圆O与EN相切于点F,........... .
求证:EB,EO是∠MEN三等分线.
 24. 已知平面直角坐标系中,点P( )和直线Ax+By+C=0(其中A,B不全为0),则点P到直线Ax+By+C=0的距离d可用公式 来计算.
24. 已知平面直角坐标系中,点P( )和直线Ax+By+C=0(其中A,B不全为0),则点P到直线Ax+By+C=0的距离d可用公式 来计算.例如:求点P(1,2)到直线y=2x+1的距离,因为直线y=2x+1可化为2x-y+1=0,其中A=2,B=-1,C=1,所以点P(1,2)到直线y=2x+1的距离为: .
根据以上材料,解答下列问题:
(1)、求点M(0,3)到直线 的距离;(2)、在(1)的条件下,⊙M的半径r = 4,判断⊙M与直线 的位置关系,若相交,设其弦长为n,求n的值;若不相交,说明理由.
-