浙教版备考2023年中考数学一轮复习67.点与圆的位置关系

试卷更新日期：2023-01-01 类型：一轮复习

进入出卷网下载

一、单选题（每题3分，共30分）

1. 已知 $⊙ O$ 的半径为 $5 cm$ ，点 $A$ 到圆心 $O$ 的距离 $OA = 3 cm$ ，则点 $A$ 与 $⊙ O$ 的位置关系（）

A、点 $A$ 在圆上 B、点 $A$ 在圆外 C、点 $A$ 在圆内 D、无法确定

查看试题解析
2. 若⊙O所在平面内一点P到⊙O上的点的最大距离为m，最小距离为n(m>n)，则此圆的半径为( )

A、 $\frac{m + n}{2}$ B、 $\frac{m - n}{2}$ C、 $\frac{m + n}{2}$ 或 $\frac{m - n}{2}$ D、m+n或m-n

查看试题解析
3. 一个点到圆的最小距离为3cm，最大距离为6cm，则该圆的直径是（）

A、1.5cm B、1.5cm或4.5cm C、4.5cm D、3cm或9cm

查看试题解析
4.
如图，MN是半径为1的⊙O的直径，点A在⊙O上，∠AMN=30°，点B为劣弧AN的中点．P是直径MN上一动点，则PA+PB的最小值为（　　）

A、 $2 \sqrt{2}$ B、 $\sqrt{2}$ C、1 D、2

查看试题解析
5. 如图，在 $△ A B C$ 中， $∠ A C B = 90 °$ ， $A B = 5$ ， $B C = 4$ ．以点 $A$ 为圆心， $r$ 为半径作圆，当点 $C$ 在 $⊙ A$ 内且点 $B$ 在 $⊙ A$ 外时， $r$ 的值可能是（）

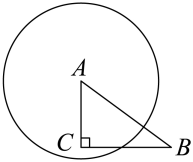A、2 B、3 C、4 D、5

查看试题解析
6. 如图，已知长方形 $A B C D$ 中， $A B = 4 ， A D = 3$ ，圆B的半径为1，圆A与圆B内切，则点 $C ， D$ 与圆A的位置关系是（）

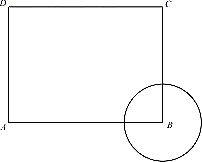A、点C在圆A外，点D在圆A内 B、点C在圆A外，点D在圆A外 C、点C在圆A上，点D在圆A内 D、点C在圆A内，点D在圆A外

查看试题解析
7. 如图所示，已知矩形 $A B C D$ 的边 $A B = 3 c m ， A D = 4 c m$ 若以点A为圆心作 $⊙ A$ ，使 $B ， C ， D$ 三点中至少有一个点在圆内，且至少有一点在圆外，则 $⊙ A$ 的半径r的取值范围是（）

A、 $3 < r < 4$ B、 $4 < r < 5$ C、 $3 < r < 5$ D、 $4 < r \leq 5$

查看试题解析
8. 如图，四边形ABCD为矩形，AB＝3，BC＝4，点P是线段BC上一动点，点M为线段AP上一点，∠ADM＝∠BAP，则BM的最小值为（）

A、 $\frac{5}{2}$ B、 $\frac{12}{5}$ C、 $\sqrt{13}$ - $\frac{3}{2}$ D、 $\sqrt{13}$ -2

查看试题解析
9. 如图，在 $R t Δ A B C$ 中， $∠ C = 9 0^{°}$ ， $A C = 4$ ， $B C = 3$ ，点O是AB的三等分点，半圆O与AC相切，M，N分别是BC与半圆弧上的动点，则MN的最小值和最大值之和是（）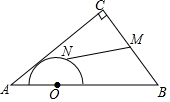

A、5 B、6 C、7 D、8

查看试题解析
10. 已知点 $P (x_{0} ， y_{0})$ 和直线 $y = k x + b$ ，求点P到直线 $y = k x + b$ 的距离d可用公式 $d = \frac{| k x_{0} - y_{0} + b |}{\sqrt{1 + k^{2}}}$ 计算．根据以上材料解决下面问题：如图， $⊙ C$ 的圆心C的坐标为 $(1 ， 1)$ ，半径为1，直线l的表达式为 $y = - 2 x + 6$ ，P是直线l上的动点，Q是 $⊙ C$ 上的动点，则 $P Q$ 的最小值是（）

A、 $\frac{3 \sqrt{5}}{5}$ B、 $\frac{3 \sqrt{5}}{5} - 1$ C、 $\frac{6 \sqrt{5}}{5} - 1$ D、2

查看试题解析

二、填空题（每题4分，共24分）

11. $⊙ O$ 的半径为2，点A到圆心的距离是3，则点A与 $⊙ O$ 的位置关系是

查看试题解析
12. 如图，在⊙O中，点A在圆内，点B在圆上，点C在圆外，若OA=3，OC=5，则OB的长度可能为(写出一个即可)

查看试题解析
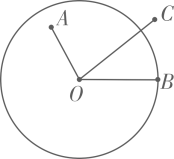13. 点 $P$ 是非圆上一点，若点 $P$ 到 $⊙ O$ 上的点的最小距离是 $4 c m$ ，最大距离是 $9 c m$ ，则 $⊙ O$ 的半径是．

查看试题解析
14. 在平面直角坐标系中，以点 $A (- 2 ， 3)$ 为圆心、 $r$ 为半径的圆与坐标轴恰好有三个公共点，那么 $r$ 的值为.

查看试题解析
15. 如图，在矩形 $A B C D$ 中， $A B = 2$ ， $B C = 4$ ，点 $E$ 为 $B C$ 上一动点，过点 $B$ 作 $A E$ 的垂线交 $A E$ 于点 $F$ ，连接 $D F$ ，则 $D F$ 的最小值是．

查看试题解析
16. 图1是邻边长为2和6的矩形，它由三个小正方形组成，将其剪拼成不重叠、无缝隙的大正方形（如图2），则图1中所标注的 $d$ 的值为；记图1中小正方形的中心为点 $A$ ， $B$ ， $C$ ，图2中的对应点为点 $A^{'}$ ， $B^{'}$ ， $C^{'}$ .以大正方形的中心 $O$ 为圆心作圆，则当点 $A^{'}$ ， $B^{'}$ ， $C^{'}$ 在圆内或圆上时，圆的最小面积为.

查看试题解析

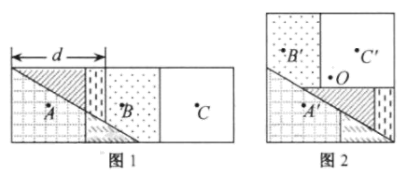
三、解答题（共8题，共66分）

17. 如图1，⊙O的半径为r（r＞0），若点P′在射线OP上，满足OP′•OP=r² ，则称点P′是点P关于⊙O的“反演点”．
如图2，⊙O的半径为4，点B在⊙O上，∠BOA=60°，OA=8，若点A′，B′分别是点A，B关于⊙O的反演点，求A′B′的长．

查看试题解析
18. 圆圆在解答问题“在矩形 $A B C D$ 中， $A B = 6 ， A D = 8 ，$ 以A为圆心作 $⊙ A$ ，使得B，C，D三点中至少有一点在 $⊙ A$ 内，有一点在 $⊙ A$ 外，求 $⊙ A$ 的半径r的取值范围？”时，答案为“ $6 < r < 8$ ”.圆圆的答案对吗？如果错误，请写出正确的解答过程.

查看试题解析
19. 如图，在矩形ABCD中，AB=6cm，AD=8cm，

(1)、若以A为圆心，6cm长为半径作⊙A（画图），则B、C、D与圆的位置关系是什么？

(2)、若作⊙A，使B、C、D三点至少有一个点在⊙A内，至少有一点在⊙A外，则⊙A的半径r的取值范围是．

查看试题解析
20. 如图，在平面直角坐标系中， $A (0 ， 4)$ 、 $B (4 ， 4)$ 、 $C (6 ， 2)$ ．

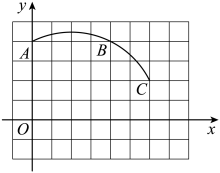(1)、在图中画出经过A、B、C三点的圆弧所在圆的圆心M的位置．

(2)、写出圆心点M的坐标为；

(3)、若 $D M = 2 \sqrt{5}$ ，判断点D与 $⊙ M$ 的位置关系．

查看试题解析
21. 如图，已知 $△$ ABC中，∠C＝90°，AC＝3，BC＝4，以点C为圆心作⊙C，半径为r．

(1)、当r取什么值时，点A在⊙C外？

(2)、当r取什么值时，点A在⊙C内，点B在⊙C外．

查看试题解析
22. 如图，△ABC中，∠ACB＝90°，AC＝6，BC＝8，点O是AB的中点．

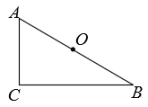(1)、若以点O为圆心，以R为半径作⊙O，且点A，B，C都在⊙O上，求R的值；

(2)、若以点B为圆心，以r为半径作⊙B，且点O，A，C中有两个点在⊙B内，有一个点在⊙B外，求r的取值范围．

查看试题解析
23. 已知二次函数y＝ax²+bx+c的图象过点A（﹣1，0），B（3，0），且与y轴交于点C（0，﹣3）.

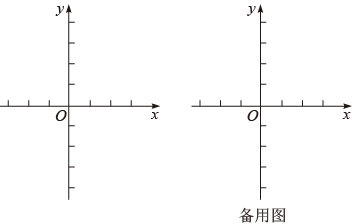(1)、求此二次函数的表达式及图象顶点D的坐标；

(2)、在此抛物线的对称轴上是否存在点E，使△ACE为Rt△，若存在，试求点E的坐标，若不存在，请说明理由；

(3)、在平面直角坐标系中，存在点P，满足PA⊥PD，求线段PB的最小值.

查看试题解析
24.

(1)、问题提出
如图1，点A为线段BC外一动点，且BC=5，AB=2，填空：当点A位于时，线段AC的长取得最大值，且最大值是；

(2)、问题探究
如图2，在Rt△ABC中，AB=AC，点D为△ABC外一点，且BD=10，CD=4，求AD的最小值；

(3)、问题解决
如图3，市政部门计划在一片足够大的空地上修建四边形的城市花园ABCD，其中AB=200米，BC=CD，BC⊥CD，BC∥AD，由于受地理位置影响，∠BAD＜90°.根据要求，现计划给该城市花园修建一条笔直的景观路，且景观路的入口定为AB的中点O，出口定为点C，为了尽可能地提高观赏体验，要求景观路OC尽可能的长，试求景观路OC最长为多少米？

查看试题解析