浙教版备考2023年中考数学一轮复习66.垂径定理及其应用
试卷更新日期:2023-01-01 类型:一轮复习
一、单选题(每题3分,共30分)
-
1. 一条排水管的截面如图所示, 已知排水管的半径 , 水面宽 , 则截面圆心O到水面的距离是( )
 A、4 B、3 C、2 D、12. 如图,AB为⊙O的弦,半径OC⊥AB于点D ,且AB=6,OD=4,则DC的长为( )
A、4 B、3 C、2 D、12. 如图,AB为⊙O的弦,半径OC⊥AB于点D ,且AB=6,OD=4,则DC的长为( ) A、1 B、2 C、2.5 D、53. 如图,是的直径,垂直于弦于点 , 的延长线交于点.若 , , 则的长是( )
A、1 B、2 C、2.5 D、53. 如图,是的直径,垂直于弦于点 , 的延长线交于点.若 , , 则的长是( )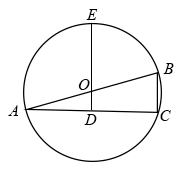 A、1 B、 C、2 D、44. 如图,已知AB是⊙O的直径,CD是OO的弦,AB⊥CD.垂足为E.若AB=26,CD=24,则∠OCE的余弦值为( )
A、1 B、 C、2 D、44. 如图,已知AB是⊙O的直径,CD是OO的弦,AB⊥CD.垂足为E.若AB=26,CD=24,则∠OCE的余弦值为( )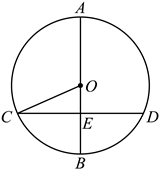 A、 B、 C、 D、5. 已知⊙O的半径为7,AB是⊙O的弦,点P在弦AB上.若PA=4,PB=6,则OP=( )A、 B、4 C、 D、56. 某仿古墙上原有一个矩形的门洞,现要将它改为一个圆弧形的门洞,圆弧所在的圆外接于矩形,如图.已知矩形的宽为2m,高为2 m,则改建后门洞的圆弧长是( )
A、 B、 C、 D、5. 已知⊙O的半径为7,AB是⊙O的弦,点P在弦AB上.若PA=4,PB=6,则OP=( )A、 B、4 C、 D、56. 某仿古墙上原有一个矩形的门洞,现要将它改为一个圆弧形的门洞,圆弧所在的圆外接于矩形,如图.已知矩形的宽为2m,高为2 m,则改建后门洞的圆弧长是( ) A、 m B、 m C、 m D、( +2)m7. 如图,将半径为8的沿折叠,弧恰好经过与垂直的半径的中点 , 则折痕长为( )
A、 m B、 m C、 m D、( +2)m7. 如图,将半径为8的沿折叠,弧恰好经过与垂直的半径的中点 , 则折痕长为( ) A、 B、 C、8 D、108. 高速公路的隧道和桥梁最多.如图是一个隧道的横截面,若它的形状是以为圆心的圆的一部分,路面米,净高米,则此圆的半径
A、 B、 C、8 D、108. 高速公路的隧道和桥梁最多.如图是一个隧道的横截面,若它的形状是以为圆心的圆的一部分,路面米,净高米,则此圆的半径 A、6米 B、米 C、7米 D、米9. 如图,C是以AB为直径的半圆O上一点,连接AC,BC,分别以AC,BC为边向外作正方形ACDE,BCFG.DE,FG, , 的中点分别是M,N,P,Q.若MP+NQ=14,AC+BC=18,则AB的长为( )
A、6米 B、米 C、7米 D、米9. 如图,C是以AB为直径的半圆O上一点,连接AC,BC,分别以AC,BC为边向外作正方形ACDE,BCFG.DE,FG, , 的中点分别是M,N,P,Q.若MP+NQ=14,AC+BC=18,则AB的长为( ) A、 B、 C、13 D、1610. 如图,⊙C 经过原点且与两坐标轴分别交于点 A 与点 B,点 B 的坐标为 ,M 是圆上一点,∠BMO=120°.⊙C的圆心C的坐标是( )
A、 B、 C、13 D、1610. 如图,⊙C 经过原点且与两坐标轴分别交于点 A 与点 B,点 B 的坐标为 ,M 是圆上一点,∠BMO=120°.⊙C的圆心C的坐标是( ) A、 B、 C、 D、
A、 B、 C、 D、二、解答题(共8题,共66分)
-
11. 把一张圆形纸片按如图方式折叠两次后展开,图中的虚线表示折痕,且折痕 , 求的半径.
 12. 《九章算术》是我国古代数学成就的杰出代表作,书中记载:“今有中,不知大小.以锯锯之,深1寸,锯道长1尺,问经几何?“其意思为:“如图,今有一圆形木材在墙中,不知其大小用锯子去锯这个木材,锯口深DE=1寸,锯道长AB=10寸,问这块圆形木材的直径是多少?”
12. 《九章算术》是我国古代数学成就的杰出代表作,书中记载:“今有中,不知大小.以锯锯之,深1寸,锯道长1尺,问经几何?“其意思为:“如图,今有一圆形木材在墙中,不知其大小用锯子去锯这个木材,锯口深DE=1寸,锯道长AB=10寸,问这块圆形木材的直径是多少?”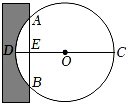 13. 如图,的直径垂直于弦于点F,点P在的延长线上,与相切于点C.
13. 如图,的直径垂直于弦于点F,点P在的延长线上,与相切于点C. (1)、求证:;(2)、若的直径为4,弦平分半径 , 求:图中阴影部分的面积.14. 石拱桥是我国古代人民勤劳和智慧的结晶(如图1),隋代建造的赵州桥距今约有1400年历史,是我国古代石拱桥的代表.如图2是根据某石拱桥的实物图画出的几何图形,桥的主桥拱是圆弧形,表示为 .桥的跨度(弧所对的弦长) ,设 所在圆的圆心为 ,半径 ,垂足为 .拱高(弧的中点到弦的距离) .连接 .
(1)、求证:;(2)、若的直径为4,弦平分半径 , 求:图中阴影部分的面积.14. 石拱桥是我国古代人民勤劳和智慧的结晶(如图1),隋代建造的赵州桥距今约有1400年历史,是我国古代石拱桥的代表.如图2是根据某石拱桥的实物图画出的几何图形,桥的主桥拱是圆弧形,表示为 .桥的跨度(弧所对的弦长) ,设 所在圆的圆心为 ,半径 ,垂足为 .拱高(弧的中点到弦的距离) .连接 .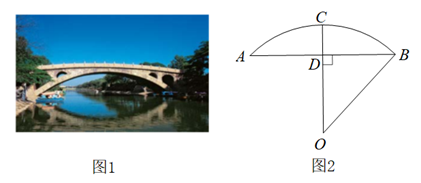 (1)、直接判断 与 的数量关系;(2)、求这座石拱桥主桥拱的半径(精确到 ).15. 如图,在 △ABC中,AB=AC ,以AB为直径的⊙O与BC交于点D,连接AD.
(1)、直接判断 与 的数量关系;(2)、求这座石拱桥主桥拱的半径(精确到 ).15. 如图,在 △ABC中,AB=AC ,以AB为直径的⊙O与BC交于点D,连接AD. (1)、求证: BD=CD;(2)、若⊙O 与AC 相切,求∠B的度数;(3)、用无刻度的直尺和圆规作出劣弧 的中点 E.(不写作法,保留作图痕迹)16. 根据以下素材,探索完成任务.
(1)、求证: BD=CD;(2)、若⊙O 与AC 相切,求∠B的度数;(3)、用无刻度的直尺和圆规作出劣弧 的中点 E.(不写作法,保留作图痕迹)16. 根据以下素材,探索完成任务.如何设计高架桥的限高及车道宽方案?
素材1
图1高架桥是一段圆弧拱形结构,图2是它的示意图.经测量,拱形跨度24m,拱顶离地面6m.

素材2
如图3,某道路规划部门计划将左侧公路分为非机动车道、机动车道一、机动车道二及绿化带四部分,原计划设计非机动车道宽3m,每条机动车道宽均3.5m.为了保证车辆的行驶安全,高架下方需要设置限高标志以警示车辆驾驶员.(限高即图中FC的高度)

素材3
如图4,由于城市道路绿化需求,道路规划部门确定新方案为在非机动车道和机动车道一之间增加一条宽为1m的绿化带,中间绿化带宽度不变,每条机动车道道宽均不小于3.25m且相等,非机动车道最高高度不小于2.5m.

问题解决
任务1
确定桥拱所在圆弧的半径.
在图2中补好图形,标注字母、数据等信息,求出桥拱所在圆弧的半径长.
任务2
探究原计划该高架桥下方机动车道一的限高要求.
在图3中画出图形,标注字母、数据等信息,计算确定机动车道一的限高高度.
任务3
拟定新方案下非机动车道和机动车车道宽度.
给出一对符合新方案要求的非机动车道和机动车道的道宽值.
(参考数值:=9.63,=11.61)
17. 综合与实践问题情境:我国东周到汉代一些出土实物上反映出一些几何作图方法,如侯马铸铜遗址出土车軎范、芯组成的(如图1),它的端面是圆形,如图2是用“矩”(带直角的角尺)确定端面圆心的方法:将“矩”的直角尖端A沿圆周移动,直到 ,在圆上标记A,B,C三点;将“矩”向右旋转,使它左侧边落在A,B点上,“矩”的另一条边与圆的交点标记为D点,这样就用“矩”确定了圆上等距离的A,B,C,D四点,连接AD,BC相交于点O,即O为圆心.
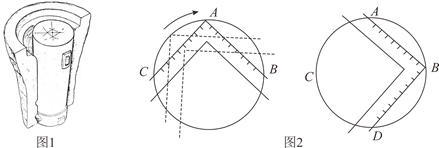
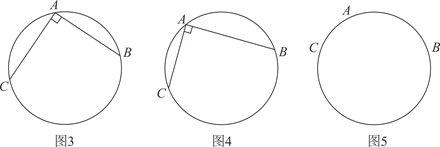 (1)、问题解决:请你根据“问题情境”中提供的方法,用三角板还原我国古代几何作图确定圆心O.如图3,点A,B,C在 上, ,且 ,请作出圆心O.(保留作图痕迹,不写作法)(2)、类比迁移:小梅受此问题的启发,在研究了用“矩”(带直角的角尺)确定端面圆心的方法后发现,如果AB和AC不相等,用三角板也可以确定圆心O.如图4,点A,B,C在 上, ,请作出圆心O.(保留作图痕迹,不写作法)(3)、拓展探究:小梅进一步研究,发现古代由“矩”度量确定圆上等距离点时存在误差,用平时学的尺规作图的方法确定圆心可以减少误差.如图5,点A,B,C是 上任意三点,请用不带刻度的直尺和圆规作出圆心O.(保留作图痕迹,不写作法)请写出你确定圆心的理由: ▲ .18. CD是以O为圆心AB为直径的半圆上的弦,E、F是弦CD上的点,线段BF与线段EO交于点G、与线段DO交于点H.
(1)、问题解决:请你根据“问题情境”中提供的方法,用三角板还原我国古代几何作图确定圆心O.如图3,点A,B,C在 上, ,且 ,请作出圆心O.(保留作图痕迹,不写作法)(2)、类比迁移:小梅受此问题的启发,在研究了用“矩”(带直角的角尺)确定端面圆心的方法后发现,如果AB和AC不相等,用三角板也可以确定圆心O.如图4,点A,B,C在 上, ,请作出圆心O.(保留作图痕迹,不写作法)(3)、拓展探究:小梅进一步研究,发现古代由“矩”度量确定圆上等距离点时存在误差,用平时学的尺规作图的方法确定圆心可以减少误差.如图5,点A,B,C是 上任意三点,请用不带刻度的直尺和圆规作出圆心O.(保留作图痕迹,不写作法)请写出你确定圆心的理由: ▲ .18. CD是以O为圆心AB为直径的半圆上的弦,E、F是弦CD上的点,线段BF与线段EO交于点G、与线段DO交于点H.

 (1)、如图1,当点E为CD中点,点F与点C重合时,若tan∠DOB= , CD=12,求EG;(2)、如图2,当弦CD∥AB,AO=10,BH=7,HG= , 求OH:OG;(3)、在(2)的条件下,若CD=16.
(1)、如图1,当点E为CD中点,点F与点C重合时,若tan∠DOB= , CD=12,求EG;(2)、如图2,当弦CD∥AB,AO=10,BH=7,HG= , 求OH:OG;(3)、在(2)的条件下,若CD=16.①求OE;
②求S△GHO—S△EFG.