浙教版备考2023年中考数学一轮复习65.圆的认识
试卷更新日期:2023-01-01 类型:一轮复习
一、单选题(每题3分,共30分)
-
1. 下列语句中不正确的有( )
①长度相等的弧是等弧;②垂直于弦的直径平分弦;③圆是轴对称图形,任何一条直径都是它的对称轴;④平分弦的直线也必平分弦所对的两条弧;⑤半圆是圆中最长的弧;⑥不在同一条直线上的三个点可以确定一个圆.
A、5个 B、4个 C、3个 D、2个2. 如图,已知☉O是ΔABD的外接圆,AB是☉O的直径,CD是0O的弦,∠ABD=58°,则∠BCD等于( ) A、16° B、32° C、58° D、64°3. 如图,为的直径,C是上的一点,若 , , 则的长度为( )
A、16° B、32° C、58° D、64°3. 如图,为的直径,C是上的一点,若 , , 则的长度为( ) A、 B、 C、 D、4. 在⊙O中,弦AB等于圆的半径,则它所对应的圆心角的度数为( )A、120° B、75° C、60° D、30°5. 如图,是的直径,点E在上,点D,C是的三等分点, , 则的度数是( )
A、 B、 C、 D、4. 在⊙O中,弦AB等于圆的半径,则它所对应的圆心角的度数为( )A、120° B、75° C、60° D、30°5. 如图,是的直径,点E在上,点D,C是的三等分点, , 则的度数是( ) A、 B、 C、 D、6. 如图,在⊙O中,点A是的中点,∠ADC=24°,则∠AOB的度数是( )
A、 B、 C、 D、6. 如图,在⊙O中,点A是的中点,∠ADC=24°,则∠AOB的度数是( )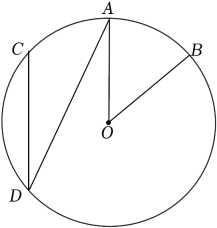 A、24° B、26° C、48° D、66°7. 将量角器按如图所示的方式放置在三角形纸板上,使点C在半圆上.点A,B的读数分别为86°,30°,则∠ACB的度数是( )
A、24° B、26° C、48° D、66°7. 将量角器按如图所示的方式放置在三角形纸板上,使点C在半圆上.点A,B的读数分别为86°,30°,则∠ACB的度数是( )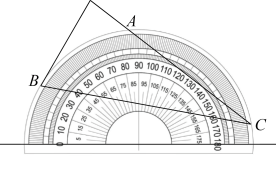 A、28° B、30° C、36° D、56°8. 如图, 内接于 ,CD是 的直径, ,则 ( )
A、28° B、30° C、36° D、56°8. 如图, 内接于 ,CD是 的直径, ,则 ( )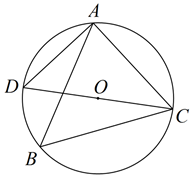 A、70° B、60° C、50° D、40°9. 如图,AB是⊙O的直径,PA与⊙O相切于点A,∠ABC=25°,OC的延长线交PA于点P,则∠P的度数是( )
A、70° B、60° C、50° D、40°9. 如图,AB是⊙O的直径,PA与⊙O相切于点A,∠ABC=25°,OC的延长线交PA于点P,则∠P的度数是( )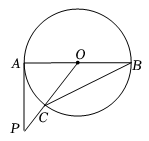 A、25° B、35° C、40° D、50°10. 如图,AB,CD是的弦,延长AB,CD相交于点P.已知 , , 则的度数是( )
A、25° B、35° C、40° D、50°10. 如图,AB,CD是的弦,延长AB,CD相交于点P.已知 , , 则的度数是( )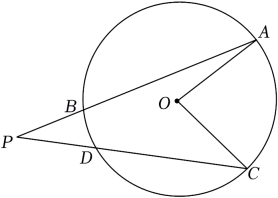 A、30° B、25° C、20° D、10°
A、30° B、25° C、20° D、10°二、填空题(每题4分,共24分)
-
11. 如图,点在上,弧的度数为.
 12. 如图,在扇形中,点C、D在上,连接、交于点E,若 , 的度数为 , 则°.
12. 如图,在扇形中,点C、D在上,连接、交于点E,若 , 的度数为 , 则°. 13. 一条弦把圆分成1:5两部分,则这条弦所对的圆心角的度数是 .14. 在⊙O中,圆心角∠AOB=90°,点O到弦AB的距离为4,则⊙O的半径的长为 .15. 如图,在平面直角坐标系中,点A,B,C的横、纵坐标都为整数,过这三个点作一条圆弧,则此圆弧的圆心坐标为 .
13. 一条弦把圆分成1:5两部分,则这条弦所对的圆心角的度数是 .14. 在⊙O中,圆心角∠AOB=90°,点O到弦AB的距离为4,则⊙O的半径的长为 .15. 如图,在平面直角坐标系中,点A,B,C的横、纵坐标都为整数,过这三个点作一条圆弧,则此圆弧的圆心坐标为 . 16. 一圆形玻璃镜面损坏了一部分,为得到同样大小的镜面,工人师傅用直角尺作如图所示的测量,测得AB=12cm,BC=5cm,则圆形镜面的半径为 .
16. 一圆形玻璃镜面损坏了一部分,为得到同样大小的镜面,工人师傅用直角尺作如图所示的测量,测得AB=12cm,BC=5cm,则圆形镜面的半径为 .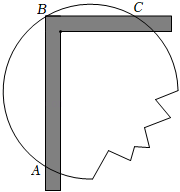
三、解答题(共8题,共66分)
-
17. 如图,学校某处空地上有A、B、C三棵树,现准备建一个圆形景观鱼池,要求A、B、C三棵树恰在圆周上,请你帮助设计鱼池,在图中作出它的鱼池轮廓,保留作图痕迹并将圆心标记为点O.
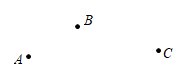 18. 证明:垂直于弦的直径平分弦以及弦所对的两条弧.
18. 证明:垂直于弦的直径平分弦以及弦所对的两条弧. 19. 某隧道施工单位准备在双向道路中间全程增加一个宽为1米的隔离带,已知隧道截面是一个半径为4米的半圆形,点O是其圆心,AE是隔离带截面,问一辆高3米,宽1.9米的卡车ABCD能通过这个隧道吗?请说明理由.
19. 某隧道施工单位准备在双向道路中间全程增加一个宽为1米的隔离带,已知隧道截面是一个半径为4米的半圆形,点O是其圆心,AE是隔离带截面,问一辆高3米,宽1.9米的卡车ABCD能通过这个隧道吗?请说明理由.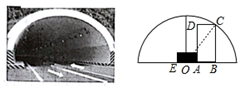 20. 如图,在以为直径的半圆中,M是半圆的中点,C是弧上的点,的延长线相交于点D,连接
20. 如图,在以为直径的半圆中,M是半圆的中点,C是弧上的点,的延长线相交于点D,连接 (1)、若 , 求的长;(2)、求证:.21. 如图,在中,B、C是的三等分点,弦相交于点E.
(1)、若 , 求的长;(2)、求证:.21. 如图,在中,B、C是的三等分点,弦相交于点E.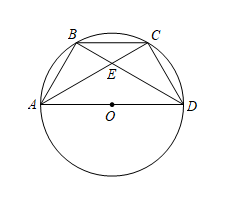 (1)、求证:;(2)、连接 , 若 , 求的度数.22. 如图,C,D是以AB为直径的半圆上的两点, , 连结BC,CD.
(1)、求证:;(2)、连接 , 若 , 求的度数.22. 如图,C,D是以AB为直径的半圆上的两点, , 连结BC,CD. (1)、求证: .(2)、若 , , 求阴影部分的面积.23. 如图1是一张圆凳的造型,已知这张圆凳的上、下底面圆的直径都是 , 高为 . 它被平行于上、下底面的平面所截得的横截面都是圆.小明画出了它的主视图,是由上、下底面圆的直径、以及、组成的轴对称图形,直线为对称轴,点、分别是、的中点,如图2,他又画出了所在的扇形并度量出扇形的圆心角 , 发现并证明了点在上.请你继续完成长的计算.
(1)、求证: .(2)、若 , , 求阴影部分的面积.23. 如图1是一张圆凳的造型,已知这张圆凳的上、下底面圆的直径都是 , 高为 . 它被平行于上、下底面的平面所截得的横截面都是圆.小明画出了它的主视图,是由上、下底面圆的直径、以及、组成的轴对称图形,直线为对称轴,点、分别是、的中点,如图2,他又画出了所在的扇形并度量出扇形的圆心角 , 发现并证明了点在上.请你继续完成长的计算.参考数据: , , , , , .
 24. 数学活动课上,老师给出这样一个题目:如图1,点C是弧上的点,于D,于E,若 , 求证:点C是弧的中点.
24. 数学活动课上,老师给出这样一个题目:如图1,点C是弧上的点,于D,于E,若 , 求证:点C是弧的中点.小波同学想到的办法是:可通过证明来完成它.
 (1)、请你们帮助小波完成证明过程:(2)、解答完老师给出的问题后,小波把老师的题进行了改变.
(1)、请你们帮助小波完成证明过程:(2)、解答完老师给出的问题后,小波把老师的题进行了改变.如图2,已知是的直径,点D,点E分别是半径 , 的中点,延长交于点F,若于D,且点C是弧的中点,求证: , 请你证明.
(3)、拓展:如图3,在(2)的条件下,点G是弧上一点,连接 , , 若 , , 求的半径长.