浙教版备考2023年中考数学一轮复习63.梯形的性质与判定

试卷更新日期：2023-01-01 类型：一轮复习

进入出卷网下载

一、单选题（每题3分，共30分）

1. 如图，把矩形ABCD沿EF翻折，点B恰好落在AD边的 $B^{'}$ 处，若AE＝2，DE＝6，∠EFB＝60°，则梯形ABFE的面积是（）

A、6 B、16 C、 $6 \sqrt{3}$ D、 $16 \sqrt{3}$

查看试题解析
2. 如图，两个一样的直角三角形重叠在一起，将其中一个三角形沿着点 $B$ 到点 $C$ 的方向平移到三角形 $D E F$ 的位置， $∠ B = 90 °$ ， $A B = 10$ ， $D H = 4$ ，平移距离为7，求阴影部分的面积为（）

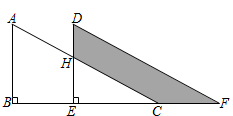A、56 B、54 C、52 D、50

查看试题解析
3. 下列命题中，真命题是（）

A、对角线互相垂直的梯形是等腰梯形 B、对角线互相垂直的平行四边形是正方形 C、对角线平分一组对角的平行四边形是菱形 D、对角线平分一组对角的梯形是直角梯形

查看试题解析
4. 如图，在四边形材料 $A B C D$ 中， $A D ∥ B C$ ， $∠ A = 90 °$ ， $A D = 9 c m$ ， $A B = 20 c m$ ， $B C = 24 c m$ .现用此材料截出一个面积最大的圆形模板，则此圆的半径是（）

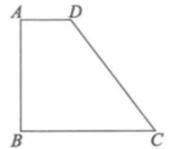A、 $\frac{110}{13} c m$ B、8cm C、 $6 \sqrt{2} c m$ D、10cm

查看试题解析
5. 如图，扇形AOB圆心角为直角，OA＝10，点C在 $\overset{⌢}{A B}$ 上，以OA，CA为邻边构造▱ACDO，边CD交OB于点E，若OE＝8，则图中两块阴影部分的面积和为（）

A、10π-8 B、5π-8 C、25π-64 D、50π-64

查看试题解析
6. 我们把梯形下底与上底的差叫做梯形的底差，梯形的高与中位线的比值叫做梯形的纵横比．如果一个腰长为 $5$ 的等腰梯形，底差等于 $6$ ，面积为 $24$ ，那么这个等腰梯形的纵横比等于（）

A、 $\frac{5}{4}$ B、 $\frac{5}{6}$ C、 $\frac{2}{3}$ D、 $\frac{3}{5}$

查看试题解析
7. 如图，在梯形ABCD中，AB∥DC ，对角线AC、BD交于点O ，下列条件中，不一定能判断梯形ABCD是等腰梯形的是（）

A、AD＝BC B、∠ABC＝∠BAD C、AB＝2DC D、∠OAB＝∠OBA

查看试题解析
8. 如图是用若干个全等的等腰梯形拼成的图形，下列说法错误的是（）

A、梯形的下底是上底的两倍 B、梯形最大角是 $120 °$ C、梯形的腰与上底相等 D、梯形的底角是 $60 °$

查看试题解析
9. 如图，点C，D是劣弧 $\overset{⌢}{A B}$ 上两点，CD∥AB，∠CAB＝45°，若AB＝6，CD＝2，则 $\overset{⌢}{A B}$ 所在圆的半径长为（）

A、 $\sqrt{17}$ B、 $\frac{16}{5}$ C、2 $\sqrt{3}$ D、 $\sqrt{10}$

查看试题解析
10. 如图，在梯形ABCD中，AD∥BC，BC＝3AD，对角线AC、BD交于点O，EF是梯形ABCD的中位线，EF与BD、AC分别交于点G、H，如果△OGH的面积为1，那么梯形ABCD的面积为（）

A、12 B、14 C、16 D、18

查看试题解析

二、填空题（每题4分，共24分）

11. 已知等腰梯形一个底角是60°，它的两底分别是6和10，那么它的腰长是．

查看试题解析
12. 在直角梯形 $A B C D$ 中， $A D // B C$ ， $∠ A = 90 °$ ， $A B = 3$ ， $C D = 6$ ，则 $∠ D$ 的度数是．

查看试题解析
13. 梯形 $A B C D$ （如图）是有由一张长方形纸折叠而成的，这个梯形的面积是 ${cm}^{2}$ ．

查看试题解析
14. 在直角三角形ABC中，∠ACB＝90°，AC＝6.将三角形ABC沿射线BC方向平移至三角形DEF处.若AG＝2，BE＝ $\frac{8}{3}$ ，则EC＝

查看试题解析
15. 如图，已知在梯形 $A B C D$ 中， $A D / / B C$ ， $A B = C D$ ，矩形 $D E F G$ 的顶点E，F，G分别在边 $A B$ ， $B C$ ， $C D$ 上，如果 $D E = 5$ ， $t a n C = \frac{5}{2}$ ，那么 $A E$ 的长为．

查看试题解析
16. 如图，点A、B在反比例函数 $y = \frac{k}{x}$ 的图象上， $A C ⊥ y$ 轴，垂足为D， $B C ⊥ A C$ .若四边形 $A O B C$ 间面积为6， $\frac{A D}{A C} = \frac{1}{2}$ ，则k的值为.

查看试题解析

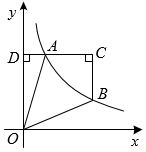
三、解答题（共8题，共66分）

17. 有一张矩形纸片 $A B C D$ ， $E$ ， $F$ 分别是边 $B C$ ， $A D$ 上的点（不与顶点重合），如图所示，若 $E F$ 将矩形 $A B C D$ 分成面积相等的两部分．求证： $A F = E C$ ．

查看试题解析
18. 某高中学校为高一新生设计的学生板凳的正面视图如图所示，其中BA=CD，BC=20cm，BC、EF平行于地面AD且到地面AD的距离分别为40cm、8cm.为使板凳两腿底端A、D之间的距离为50cm，那么横梁EF应为多长？（材质及其厚度等暂忽略不计）.

查看试题解析
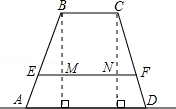19. 如图，在梯形ABCD中，AD∥BC，AB＝DC＝8，∠B＝60°，BC＝12，连接AC．

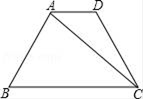(1)、求tan∠ACB的值；

(2)、若M、N分别是AB、DC的中点，连接MN，求线段MN的长．

查看试题解析
20. 如图，已知 $△ A B C$ 的面积为16， $B C = 8$ .现将 $△ A B C$ 沿直线BC向右平移a个单位到 $△ D E F$ 的位置.

(1)、连接AD，四边形ABFD的面积为32时，求a的值；

(2)、连接AE、AD，当 $A B = 5$ ， $a = 5$ 时，试判断 $△ A D E$ 的形状，并说明理由.

查看试题解析
21. 在四边形ABCD中， $A D ∥ B C$ ， $∠ B = 90 °$ ， $A B = 8 cm$ ， $A D = 24 cm$ ， $B C = 26 cm$ .点P从点A出发，以1cm/s的速度向点D运动，点Q从点C出发，以3cm/s的速度向点B同时运动.规定其中一个动点到达端点时，另一个动点也随之停止运动.设P，Q运动的时间为t s.

(1)、若点P和点Q同时运动了6秒，PQ与CD有什么数量关系？并说明理由；

(2)、在整个运动过程中是否存在t值，使得四边形PQBA是矩形？若存在，请求出t值；若不存在，请说明理由；

(3)、在整个运动过程中，是否存在一个时间，使得四边形PQBA的面积是四边形ABCD面积的一半，若存在，请直接写出值；若不存在，请说明理由.

查看试题解析
22.

(1)、如图，四边形ABCD的面积是m，E，F，G，H分别是边AB，BC，CD，AD的中点，则图中阴影部分的面积是（用含m的代数式表示）．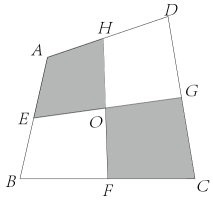

(2)、如图，把等腰梯形ABCD放在平面直角坐标系中，已知三个顶点的坐标分别是A（－2，0），B（6，0），C（4，4），画出经过顶点D并且平分梯形面积的直线，并求出它的表达式．

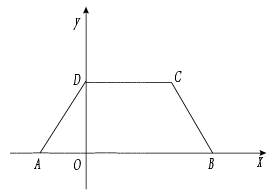(3)、如图，在四边形ABCD中，AD∥BC，AB＞CD，是否存在过点A的一条直线将四边形ABCD的面积平分？如果存在，请画出符合条件的直线，并说明你的作法和理由；如果不存在，也请说明理由．

查看试题解析
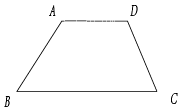23. 在等腰梯形ABCD中，DC//AB，AB= 6， $t a n B = 2 \sqrt{2}$ ，过点A作AH⊥BC，垂足为点H．

(1)、当点C与点H重合时（如图），求线段BC的长；

(2)、当点C不与点H重合时，联结AC，作△ACH的外接圆O．
①当点C在BH的延长线上时（如图），设CH=x，CD = y，求y与x的函数解析式，并写出定义域；
②延长CD交圆O于点G，如果△ACH与△ACG全等，求CD的长

查看试题解析
24. 如图，在等腰梯形ABCD中，ADllBC，BC=4 $\sqrt{3}$ ，AD= $\sqrt{3}$ ，∠B=30°，直角三角板含30°角的顶点E在边BC上移动，一直角边始终经过点A，斜边与CD交于点F.设BE=x，CF=y。

(1)、点E在边BC上运动的过程中，图中是否有相似三角形，请证明；

(2)、求y关于x的函数解析式，并写出定义域；

(3)、连接AF，点E在移动过程中，△AEF能否成为直角三角形，若能，请求出x的值；若不能，请说明理由。

查看试题解析