浙教版备考2023年中考数学一轮复习62.正方形的性质与判定
试卷更新日期:2023-01-01 类型:一轮复习
一、单选题(每题3分,共30分)
-
1. 若顺次连接四边形 各边的中点所得的四边形是正方形,则四边形 的两条对角线 一定是( )A、互相平分 B、互相垂直 C、互相平分且相等 D、互相垂直且相等2. 如图,正方形的对角线交于点O,点E是直线上一动点.若 , 则的最小值是( )
 A、 B、 C、 D、3. 如图,在矩形中,对角线、交于点 , 添加下列一个条件,能使矩形成为正方形的是
A、 B、 C、 D、3. 如图,在矩形中,对角线、交于点 , 添加下列一个条件,能使矩形成为正方形的是 A、 B、 C、 D、4. 如图,正方形ABCD的面积为3,点E在边CD上, 且CE = 1,∠ABE的平分线交AD于点F,点M,N分别是BE,BF的中点,则MN的长为( )
A、 B、 C、 D、4. 如图,正方形ABCD的面积为3,点E在边CD上, 且CE = 1,∠ABE的平分线交AD于点F,点M,N分别是BE,BF的中点,则MN的长为( )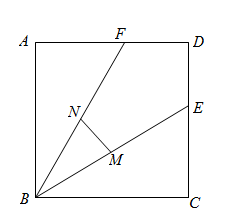 A、 B、 C、 D、5. 如图,在正方形中,和交于点O,过点O的直线交于点(E不与A,B重合),交于点F.以点O为圆心,为半径的圆交直线于点M,N.若 , 则图中阴影部分的面积为( )
A、 B、 C、 D、5. 如图,在正方形中,和交于点O,过点O的直线交于点(E不与A,B重合),交于点F.以点O为圆心,为半径的圆交直线于点M,N.若 , 则图中阴影部分的面积为( )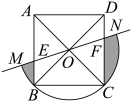 EA、 B、 C、 D、6. 如图所示,面积为5的正方形的顶点在数轴上,且点表示的数为1,若点在数轴上点在点左侧 , 且 , 则点所表示的数为( )
EA、 B、 C、 D、6. 如图所示,面积为5的正方形的顶点在数轴上,且点表示的数为1,若点在数轴上点在点左侧 , 且 , 则点所表示的数为( )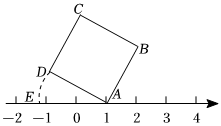 A、 B、 C、 D、7. 如图1,直角三角形纸片的一条直角边长为1,斜边为3.把它们按图2,拼摆正方形,纸片在结合部分不重叠无缝隙,则图2的中间空白部分,即四边形ABCD的面积为( )
A、 B、 C、 D、7. 如图1,直角三角形纸片的一条直角边长为1,斜边为3.把它们按图2,拼摆正方形,纸片在结合部分不重叠无缝隙,则图2的中间空白部分,即四边形ABCD的面积为( ) A、 B、9 C、 D、以上都不对8. 如图,在正方形ABCD中放入两个相同小正方形纸片,重叠部分记为①,点E,F的位置如图所示,若D,F,E三点共线,则正方形ABCD与①的面积比为( )
A、 B、9 C、 D、以上都不对8. 如图,在正方形ABCD中放入两个相同小正方形纸片,重叠部分记为①,点E,F的位置如图所示,若D,F,E三点共线,则正方形ABCD与①的面积比为( ) A、9+4 B、2 C、3 D、99. “方胜”是中国古代妇女的一种发饰,其图案由两个全等正方形相叠组成,寓意是同心吉祥.如图,将边长为2cm的正方形ABCD沿对角线BD方向平移1cm得到正方形A′B′C′D′,形成一个“方胜”图案,则点D,B′之间的距离为( )
A、9+4 B、2 C、3 D、99. “方胜”是中国古代妇女的一种发饰,其图案由两个全等正方形相叠组成,寓意是同心吉祥.如图,将边长为2cm的正方形ABCD沿对角线BD方向平移1cm得到正方形A′B′C′D′,形成一个“方胜”图案,则点D,B′之间的距离为( )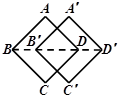 A、1cm B、2cm C、( -1)c. D、(2 -1)cm10. 如图,正方形位于第一象限, , 顶点A,C在直线上,且点A的横坐标为1,若双曲线与正方形有两个交点,则k的取值范围是( )
A、1cm B、2cm C、( -1)c. D、(2 -1)cm10. 如图,正方形位于第一象限, , 顶点A,C在直线上,且点A的横坐标为1,若双曲线与正方形有两个交点,则k的取值范围是( ) A、或 B、 C、 D、或
A、或 B、 C、 D、或二、填空题(每题4分,共24分)
-
11. 如图所示,将两个边长为2的正方形沿虚线剪开(如图甲),拼接成一个大的正方形(如图乙),则图乙中大正方形的边长为 .
 12. 如图,将边长为3的正方形ABCD沿其对角线AC平移,使A的对应点A′满足AA′=AC,则所得正方形与原正方形重叠部分的面积是 .
12. 如图,将边长为3的正方形ABCD沿其对角线AC平移,使A的对应点A′满足AA′=AC,则所得正方形与原正方形重叠部分的面积是 .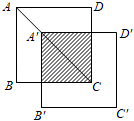 13. 如图,在直角坐标系中,边长为2个单位长度的正方形绕原点O逆时针旋转 , 再沿y轴方向向上平移1个单位长度,则点的坐标为 .
13. 如图,在直角坐标系中,边长为2个单位长度的正方形绕原点O逆时针旋转 , 再沿y轴方向向上平移1个单位长度,则点的坐标为 .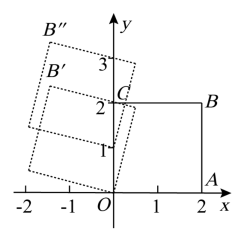 14. 如图,以正方形的中心为原点建立平面直角坐标系,点A的坐标为 , 则点D的坐标为 .
14. 如图,以正方形的中心为原点建立平面直角坐标系,点A的坐标为 , 则点D的坐标为 . 15. 如图,把边长为1:2的矩形ABCD沿长边BC,AD的中点E,F对折,得到四边形ABEF,点G,H分别在BE,EF上,且BG=EH=BE=2,AG与BH交于点O,N为AF的中点,连接ON,作OM⊥ON交AB于点M,连接MN,则tan∠AMN=.
15. 如图,把边长为1:2的矩形ABCD沿长边BC,AD的中点E,F对折,得到四边形ABEF,点G,H分别在BE,EF上,且BG=EH=BE=2,AG与BH交于点O,N为AF的中点,连接ON,作OM⊥ON交AB于点M,连接MN,则tan∠AMN=.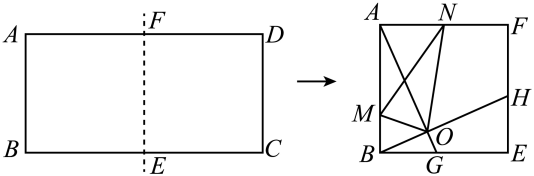 16. 如图,已知点 , , , 在函数位于第二象限的图象上,点 , , , 在函数位于第一象限的图象上,点 , , , 在轴的正半轴上,若四边形、 , , 都是正方形,则正方形的对角线长为 .
16. 如图,已知点 , , , 在函数位于第二象限的图象上,点 , , , 在函数位于第一象限的图象上,点 , , , 在轴的正半轴上,若四边形、 , , 都是正方形,则正方形的对角线长为 .
三、作图题(共8分)
-
17. 如图为方格,每个小正方形的边长都为1.
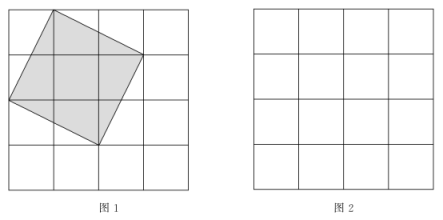 (1)、图1中阴影正方形的面积为 , 边长为;(2)、请在图2中画出一个与图1中阴影部分面积不相等的正方形,并求出所画正方形的边长.要求所画正方形满足以下条件:①正方形的边长为无理数 ②正方形的四个顶点均在网格格点处.
(1)、图1中阴影正方形的面积为 , 边长为;(2)、请在图2中画出一个与图1中阴影部分面积不相等的正方形,并求出所画正方形的边长.要求所画正方形满足以下条件:①正方形的边长为无理数 ②正方形的四个顶点均在网格格点处.四、解答题(共7题,共58分
-
18. 如图,在菱形中,对角线 , 相交于点 , 点 , 在对角线上,且 , .
求证:四边形是正方形.
 19. 如图,边长为的正方形中,是的中点,是上一点,且 , 求证:
19. 如图,边长为的正方形中,是的中点,是上一点,且 , 求证: 20. 在平面直角坐标系中,若点P的坐标为(x,y),则定义:d(x,y)=|x|+|y|为点P到坐标原点O的“折线距离”.
20. 在平面直角坐标系中,若点P的坐标为(x,y),则定义:d(x,y)=|x|+|y|为点P到坐标原点O的“折线距离”. (1)、若已知P(-2,3),则点P到坐标原点O的“折线距离”d(-2,3)=;(2)、若点P(x,y)满足2x+y=0,且点P到坐标原点O的“折线距离”d(x,y)=6,求出P的坐标;(3)、若点P到坐标原点O的“折线距离”d(x,y)=3,试在坐标系内画出所有满足条件的点P构成的图形,并求出该图形的所围成封闭区域的面积.21. 如图,四边形ABCD中,对角线AC与BD交于点O,且OA=OB=OC=OD= AB.
(1)、若已知P(-2,3),则点P到坐标原点O的“折线距离”d(-2,3)=;(2)、若点P(x,y)满足2x+y=0,且点P到坐标原点O的“折线距离”d(x,y)=6,求出P的坐标;(3)、若点P到坐标原点O的“折线距离”d(x,y)=3,试在坐标系内画出所有满足条件的点P构成的图形,并求出该图形的所围成封闭区域的面积.21. 如图,四边形ABCD中,对角线AC与BD交于点O,且OA=OB=OC=OD= AB.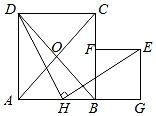 (1)、求证:四边形ABCD是正方形;(2)、若H是边AB上一点(H与A,B不重合),连接DH,将线段DH绕点H顺时针旋转90°,得到线段HE,过点E分别作BC及AB延长线的垂线,垂足分别为F,G.设四边形BGEF的面积为s1 , 以HB,BC为邻边的矩形的面积为s2 , 且s1=s2.当AB=2时,求AH的长.22. 如图所示,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD,BE.
(1)、求证:四边形ABCD是正方形;(2)、若H是边AB上一点(H与A,B不重合),连接DH,将线段DH绕点H顺时针旋转90°,得到线段HE,过点E分别作BC及AB延长线的垂线,垂足分别为F,G.设四边形BGEF的面积为s1 , 以HB,BC为邻边的矩形的面积为s2 , 且s1=s2.当AB=2时,求AH的长.22. 如图所示,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD,BE.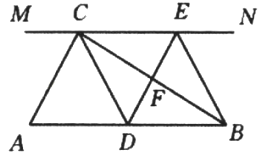 (1)、求证:CE=AD;(2)、当D为AB中点时,四边形BECD是什么特殊的四边形?说明你的理由;(3)、若D为AB中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?请说明你的理由.23. 【经典回顾】
(1)、求证:CE=AD;(2)、当D为AB中点时,四边形BECD是什么特殊的四边形?说明你的理由;(3)、若D为AB中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?请说明你的理由.23. 【经典回顾】梅文鼎是我国清初著名的数学家,他在《勾股举隅》中给出多种证明勾股定理的方法图1是其中一种方法的示意图及部分辅助线.

在中, , 四边形、和分别是以的三边为一边的正方形.延长和 , 交于点 , 连接并延长交于点 , 交于点 , 延长交于点 .
(1)、证明:;(2)、证明:正方形的面积等于四边形的面积;(3)、请利用(2)中的结论证明勾股定理.(4)、【迁移拓展】如图2,四边形和分别是以的两边为一边的平行四边形,探索在下方是否存在平行四边形 , 使得该平行四边形的面积等于平行四边形、的面积之和.若存在,作出满足条件的平行四边形(保留适当的作图痕迹);若不存在,请说明理由.
24. 某校数学活动小组在一次活动中,对一个数学问题作如下探究:

 (1)、问题发现:如图1,在等边△ABC中,点P是边BC上任意一点,连接AP,以AP为边作等边△APQ,连接CQ.求证:BP= CQ;(2)、变式探究:如图2,在等腰△ABC中,AB=BC,点P是边BC上任意一点,以AP为腰作等腰△APQ,使AP =PQ,∠APQ =∠ABC,连接CQ.判断∠ABC和∠ACQ的数量关系,并说明理由;(3)、解决问题:如图3,在正方形ADBC中,点P是边BC上一点,以AP为边作正方形 APEF,Q是正方形APEF的中心,连接CQ.若正方形APEF的边长为6, , 求正方形ADBC的边长.
(1)、问题发现:如图1,在等边△ABC中,点P是边BC上任意一点,连接AP,以AP为边作等边△APQ,连接CQ.求证:BP= CQ;(2)、变式探究:如图2,在等腰△ABC中,AB=BC,点P是边BC上任意一点,以AP为腰作等腰△APQ,使AP =PQ,∠APQ =∠ABC,连接CQ.判断∠ABC和∠ACQ的数量关系,并说明理由;(3)、解决问题:如图3,在正方形ADBC中,点P是边BC上一点,以AP为边作正方形 APEF,Q是正方形APEF的中心,连接CQ.若正方形APEF的边长为6, , 求正方形ADBC的边长.
-