浙教版备考2023年中考数学一轮复习60.矩形的性质与判定
试卷更新日期:2023-01-01 类型:一轮复习
一、单选题(每题3分,共30分)
-
1. 要检验一个四边形的桌面是否为矩形,可行的测量方案是( )A、测量两条对角线是否相等 B、度量两个角是否是90° C、测量两条对角线的交点到四个顶点的距离是否相等 D、测量两组对边是否分别相等2. 如图所示,将一矩形纸片沿AB折叠,已知 , 则( )
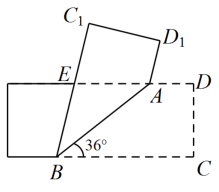 A、48° B、66° C、72° D、78°3. 如图,矩形ABCD为一个正在倒水的水杯的截面图,杯中水面与CD的交点为E,当水杯底面BC与水平面的夹角为27°时,∠AED的大小为( )
A、48° B、66° C、72° D、78°3. 如图,矩形ABCD为一个正在倒水的水杯的截面图,杯中水面与CD的交点为E,当水杯底面BC与水平面的夹角为27°时,∠AED的大小为( ) A、27° B、53° C、57° D、63°4. 如图,E、F、G、H分别是矩形的边AB、BC、CD、AD上的点,AH=CF,AE=CG,∠EHF=60°,∠GHF=45°.若AH=2,AD=5+ . 则四边形EFGH的周长为( )
A、27° B、53° C、57° D、63°4. 如图,E、F、G、H分别是矩形的边AB、BC、CD、AD上的点,AH=CF,AE=CG,∠EHF=60°,∠GHF=45°.若AH=2,AD=5+ . 则四边形EFGH的周长为( )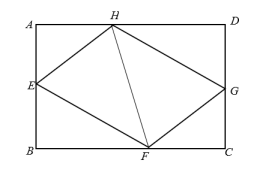 A、 B、 C、 D、5. 如图,四边形和四边形是两个矩形,点B在边上,若 , 则矩形的面积为( )
A、 B、 C、 D、5. 如图,四边形和四边形是两个矩形,点B在边上,若 , 则矩形的面积为( ) A、3 B、 C、 D、66. 如图,在中, , 分别以点,点为圆心以大于为半径画弧,两弧交于 , , 连接交于点 , 连接 , 以为圆心,长为半径作弧,交于点,则:( )
A、3 B、 C、 D、66. 如图,在中, , 分别以点,点为圆心以大于为半径画弧,两弧交于 , , 连接交于点 , 连接 , 以为圆心,长为半径作弧,交于点,则:( ) A、1: B、1:2 C、1: D、1:7. 如图,矩形A1B1C1D1在矩形ABCD的内部,且B1C1⊥BC,点B1 , D1在对角线BD的异侧.连结BB1 , DB1 , BD1 , DD1 , 若矩形ABCD∼矩形A1B1C1D1 , 且两个矩形的周长已知.只需要知道下列哪个值就一定可以求得四边形B1BD1D的面积( )
A、1: B、1:2 C、1: D、1:7. 如图,矩形A1B1C1D1在矩形ABCD的内部,且B1C1⊥BC,点B1 , D1在对角线BD的异侧.连结BB1 , DB1 , BD1 , DD1 , 若矩形ABCD∼矩形A1B1C1D1 , 且两个矩形的周长已知.只需要知道下列哪个值就一定可以求得四边形B1BD1D的面积( ) A、矩形ABCD的面积 B、∠B1BD1的度数 C、四边形B1BD1D的周长 D、BB1的长度8. 如图,在矩形ABCD中,BC=20cm,点P和点Q分别从点B和点D同时出发,按逆时针方向沿矩形ABCD的边运动,点P和点Q的速度分别为3cm/s和2cm/s,当四边形ABPQ初次为矩形时,点P和点Q运动的时间为( )秒.
A、矩形ABCD的面积 B、∠B1BD1的度数 C、四边形B1BD1D的周长 D、BB1的长度8. 如图,在矩形ABCD中,BC=20cm,点P和点Q分别从点B和点D同时出发,按逆时针方向沿矩形ABCD的边运动,点P和点Q的速度分别为3cm/s和2cm/s,当四边形ABPQ初次为矩形时,点P和点Q运动的时间为( )秒. A、2 B、3 C、4 D、59. 西周数学家商高总结了用“矩”(如图1)测量物高的方法:把矩的两边放置成如图2的位置,从矩的一端A(人眼)望点E,使视线通过点C,记人站立的位置为点B,量出BG长,即可算得物高EG.令BG=x(m), EG=y(m),若a=30cm,b=60cm,AB=1.6m,则y关于x的函数表达式为( )
A、2 B、3 C、4 D、59. 西周数学家商高总结了用“矩”(如图1)测量物高的方法:把矩的两边放置成如图2的位置,从矩的一端A(人眼)望点E,使视线通过点C,记人站立的位置为点B,量出BG长,即可算得物高EG.令BG=x(m), EG=y(m),若a=30cm,b=60cm,AB=1.6m,则y关于x的函数表达式为( )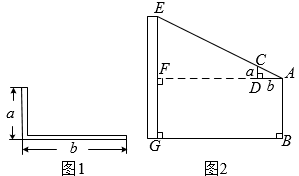 A、 B、 C、 D、10. 如图,四边形ABCD为矩形,AB=3,BC=4,点P是线段BC上一动点,点M为线段AP上一点,∠ADM=∠BAP,则BM的最小值为( )
A、 B、 C、 D、10. 如图,四边形ABCD为矩形,AB=3,BC=4,点P是线段BC上一动点,点M为线段AP上一点,∠ADM=∠BAP,则BM的最小值为( ) A、 B、 C、- D、-2
A、 B、 C、- D、-2二、填空题(每题4分,共24分)
-
11. 已知两边长为5和12,则其斜边上的中线为.12. 如图,在Rt△ABC中,∠ACB=90°,通过尺规作图得到的直线MN分别交AB,AC于D,E,连接CD.若 ,则CD=.
 13. 在矩形中,作的平分线交直线于点E,则是度.14. 如图,四边形为矩形, , 点E为边上一点,将沿翻折,点C的对应点为点F,过点F作的平行线交于点G,交直线于点H.若点G是边的三等分点,则的长是 .
13. 在矩形中,作的平分线交直线于点E,则是度.14. 如图,四边形为矩形, , 点E为边上一点,将沿翻折,点C的对应点为点F,过点F作的平行线交于点G,交直线于点H.若点G是边的三等分点,则的长是 . 15. 如图,有两张矩形纸片ABCD和EFGH,AB=EF=2cm,BC=FG=8cm.将两纸片按如图所示叠放,使点D与点G重合,且重叠部分为平行四边形.当两张纸片交叉所成的角记为α,当α=30°时,BM=;当α最小时,重叠部分的面积为 .
15. 如图,有两张矩形纸片ABCD和EFGH,AB=EF=2cm,BC=FG=8cm.将两纸片按如图所示叠放,使点D与点G重合,且重叠部分为平行四边形.当两张纸片交叉所成的角记为α,当α=30°时,BM=;当α最小时,重叠部分的面积为 . 16. 如图1是某学校食堂墙壁上“光盘行动,从我做起”的长方形宣传画,画的左侧为一个圆盘上摆放一双筷子,画的下边缘为水平线,图2是其示意图,水平线l上的点A在圆心O的正下方,筷子与右下方交于B,C两点,线段 , 分别垂直l于点D,E.测得 , , 则圆盘的半径为.
16. 如图1是某学校食堂墙壁上“光盘行动,从我做起”的长方形宣传画,画的左侧为一个圆盘上摆放一双筷子,画的下边缘为水平线,图2是其示意图,水平线l上的点A在圆心O的正下方,筷子与右下方交于B,C两点,线段 , 分别垂直l于点D,E.测得 , , 则圆盘的半径为.
三、解答题(共8题,共66分)
-
17. 如图,在中, . 作出点D,使四边形是矩形.(要求:尺规作图,不写作法,保留作图痕迹)
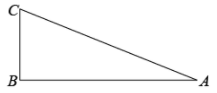 18. 如图, , 是的中位线, , 连接 , , 求证: .
18. 如图, , 是的中位线, , 连接 , , 求证: . 19. 如图,在平行四边形ABCD中,DE⊥AB,点F在AB的延长线上,且CF⊥AB.
19. 如图,在平行四边形ABCD中,DE⊥AB,点F在AB的延长线上,且CF⊥AB.求证:四边形CDEF是矩形.
 20. 如图, 中, , 相交于点 , , 分别是 , 的中点.
20. 如图, 中, , 相交于点 , , 分别是 , 的中点. (1)、求证: ;(2)、设 ,当 为何值时,四边形 是矩形?请说明理由.21. 如图,将矩形ABCD沿对角线AC折叠,点B的对应点为E,AE与CD交于点F.
(1)、求证: ;(2)、设 ,当 为何值时,四边形 是矩形?请说明理由.21. 如图,将矩形ABCD沿对角线AC折叠,点B的对应点为E,AE与CD交于点F.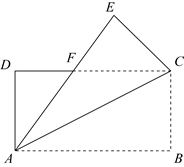 (1)、求证: ;(2)、若 ,求 的度数.22. “五一”节期间,许多露营爱好者在我市郊区露营,为遮阳和防雨会搭建一种“天幕”,其截面示意图是轴对称图形,对称轴是垂直于地面的支杆 , 用绳子拉直后系在树干上的点处,使得 , , 在一条直线上,通过调节点的高度可控制“天幕”的开合,m,m.
(1)、求证: ;(2)、若 ,求 的度数.22. “五一”节期间,许多露营爱好者在我市郊区露营,为遮阳和防雨会搭建一种“天幕”,其截面示意图是轴对称图形,对称轴是垂直于地面的支杆 , 用绳子拉直后系在树干上的点处,使得 , , 在一条直线上,通过调节点的高度可控制“天幕”的开合,m,m.
(参考数据: , , , )
(1)、天晴时打开“天幕”,若 , 求遮阳宽度(结果精确到0.1m);(2)、下雨时收拢“天幕”,从65°减少到45°,求点下降的高度(结果精确到0.1m).23. 如图,在矩形ABCD中,AB=16cm,BC=6cm,点P从点A出发,以3cm/s的速度向点B移动,一直到达点B为止;同时,点Q从点C出发,以2cm/s的速度向点D移动.当其中一个点停止移动时,另一个点也随之停止,设移动时间为ts,连接PQ. (1)、当t=2时,求PQ的长;(2)、当PQ=10cm时,求t的值.24. 如图,在中, , 平分的外角 , 于点D,过D点作平行交于点E.点P在线段上,点Q在直线上,且 , 连接 , 作P点关于直线的对称点 , 连接.
(1)、当t=2时,求PQ的长;(2)、当PQ=10cm时,求t的值.24. 如图,在中, , 平分的外角 , 于点D,过D点作平行交于点E.点P在线段上,点Q在直线上,且 , 连接 , 作P点关于直线的对称点 , 连接. (1)、当P在中点时,t =;连接 , 则此时与位置关系为(2)、①求线段的长:
(1)、当P在中点时,t =;连接 , 则此时与位置关系为(2)、①求线段的长:②将线段绕着平面上某个点旋转后,使的两个对应点、落在的边上,求点A到对应点的距离;
(3)、如图,当的一边与的或边平行时,求所有满足条件的t的值.