2022-2023学年浙教版数学七年级上册期末模拟试卷

试卷更新日期：2022-12-31 类型：期末考试

进入出卷网下载

一、单选题（每题4分，共40分）

1. 将 $1000000$ 用科学记数法表示为（）

A、 $1 \times 1 0^{6}$ B、 $0.1 \times 1 0^{6}$ C、 $0.1 \times 1 0^{7}$ D、 $1 × 1 0^{7}$

查看试题解析
2. 在-2，0，3，π这四个数中，既不是正数，也不是负数的是（）

A、-2 B、0 C、3 D、π

查看试题解析
3. 下列算式中，正确的是（）

A、 $a^{4} + a^{2} = a^{6}$ B、 $- a^{3} \cdot a^{5} = - a^{8}$ C、 ${(- a^{2})}^{6} = - a^{12}$ D、 ${(3 a^{2})}^{3} = 9 a^{6}$

查看试题解析
4. 已知 $(k - 1) x^{k^{2}} + 3 = 0$ 是关于x的一元一次方程，则 $k$ 的值是（）

A、-1 B、1 C、-1或1 D、0

查看试题解析
5. 根据下列语句画相应的几何图形，正确的是（）

A、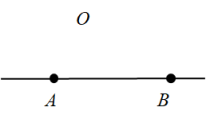点O在直线AB上 B、直线AB与CD都经过点O C、在∠ABC内部画射线BP D、延长BA到点C，使BC＝2AB

查看试题解析
6. 如图所示，面积为5的正方形 $A B C D$ 的顶点 $A$ 在数轴上，且点 $A$ 表示的数为1，若点 $E$ 在数轴上 $($ 点 $E$ 在点 $A$ 左侧 $)$ ，且 $A D = A E$ ，则点 $E$ 所表示的数为（）

A、 $\sqrt{5}$ B、 $- \sqrt{5}$ C、 $- \sqrt{5} - 1$ D、 $- \sqrt{5} + 1$

查看试题解析
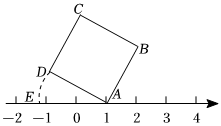7. 《算法统宗》中有如下的类似问题：“哑子来买肉，难言钱数目，一斤少二十五，八两多十五，试问能算者，合与多少肉”，意思是一个哑巴来买肉，说不出钱的数目，买一斤（16两）还差二十五文钱，买八两多十五文钱，设哑巴所带的钱数为x文，则可列方程为（）

A、 $x - 15 = 2 (x + 25)$ B、 $x - 25 = 2 (x + 15)$ C、 $x + 15 = 2 (x - 25)$ D、 $x + 25 = 2 (x - 15)$

查看试题解析
8. 根据以下程序，当输入 $x = \sqrt{7}$ 时，输出的结果是（）

A、0 B、1 C、 $\sqrt{2}$ D、 $\sqrt{3}$

查看试题解析
9. 在一个3×3的方格中填写9个数字，使得每行每列每条对角线上的三个数之和相等，得到的3×3的方格称为一个三阶幻方．如方格中填写了一些数和字母，为使该方格构成一个三阶幻方，则x+2y的值是（）．

A、15 B、17 C、19 D、21

查看试题解析
10. 如图，A、O、B两点在数轴上对应的数分别为﹣20、0、40，C点在A、B之间，在A、B两点处各放一个挡板，M、N两个小球同时从C处出发，M以2个单位/秒的速度向数轴负方向运动，N以4个单位/秒的速度向数轴正方向运动，碰到挡板后则反方向运动，速度大小不变．设两个小球运动的时间为t秒钟（0＜t＜40），当M小球第一次碰到A挡板时，N小球刚好第一次碰到B挡板．则：①C点在数轴上对应的数为0；②当10＜t＜25时，N在数轴上对应的数可以表示为80﹣4t；③当25＜t＜40时，2MA+NB始终为定值160；④只存在唯一的t值，使3MO＝NO，以上结论正确的有（　　）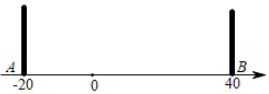

A、①②③④ B、①③ C、②③ D、①②④

查看试题解析

二、填空题（11-16每题3分，17-18每题5分）

11. 若 $| a - 4 | + | b + 3 | = 0$ ，则 $a b =$ ．

查看试题解析
12. 温州十二月份某天上午10时气温为 $5 ℃$ ，过 $4$ 小时后气温上升了 $4 ℃$ ，又过了3小时气温又下降了 $29 ℃$ ，则此时的气温是 $℃ .$

查看试题解析
13. 有理数3.1415精确到百分位结果是.

查看试题解析
14. 我们知道： $| 5 - 2 |$ 表示5与2的差的绝对值，也可理解为5与2两数在数轴上所对应的两点之间的距离； $| 5 + 2 |$ 也可以看成 $| 5 - (- 2) |$ ，表示5与 $- 2$ 之差的绝对值，也可理解为数轴上表示5与 $- 2$ 两数在数轴上所对应的两点之间的距离事实上，数轴上表示有理数 $a ， b$ 的点 $A ， B$ 的距离均可以用 $| a - b |$ 来计算.根据以上材料，则使 $| x + 3 | + | x - 4 | = 7$ 的所有整数x的和是.

查看试题解析
15. 中百超市推出如下优惠方案：
⑴一次性购物不超过 100 元，不享受优惠
⑵一次性购物超过 100 元，但不超过 300 元一律 9 折；
⑶一次性购物超过 300 元一律 8 折．某人两次购物分别付款 80 元、252 元，如果他将这两次所购商品一次性购买，则应付款．

查看试题解析
16. 计算： $| \frac{1}{2018} - \frac{1}{2017} | + | \frac{1}{2017} - \frac{1}{2016} | - | \frac{1}{2018} - \frac{1}{2016} | =$ .

查看试题解析
17. 如果关于 $x$ 的方程 $[\frac{x}{2}] + [\frac{2 x}{3}] + [\frac{3 x}{5}] = \frac{k}{7} x$ 有正整数解，那么正整数 $k$ 的所有可能取值之和为．

查看试题解析
18. 两个边长分别为a和b的正方形如图放置（图1），其未叠合部分（阴影）面积为 $S_{1}$ ；若再在图1中大正方形的右下角摆放一个边长为b的小正方形（如图2），两个小正方形叠合部分（阴影）面积为 $S_{2}$ .当 $S_{1}$ ＋ $S_{2}$ ＝40时，则图3中阴影部分的面积 $S_{3} =$ .

查看试题解析

三、计算题（共2题，共20分）

19.

(1)、计算： $- 3^{2} + 5 \times (- \frac{8}{5}) - {(- 4)}^{2} \div (- 8)$ ；

(2)、解方程： $\frac{0.1 x - 0.2}{0.02} - \frac{x + 1}{0.5} = 3$ ．

查看试题解析
20. 定义一种新运算：a@b=b²-ab，如：1@2=2²-1×2=2，

(1)、求-3@ $\frac{1}{2}$ ；

(2)、若x@3=-3，求x值。

查看试题解析

四、作图题（共2题，共16分）

21. 如图所示，已知线段AB，点P是线段AB外一点．按要求画图，保留作图痕迹；

(1)、作射线PA，作直线PB；

(2)、延长线段AB至点C，使得AC=2AB．

查看试题解析
22. 如图，4×4的方格中，每个小正方形的边长为1．

⑴图①中正方形ABCD的边长为；

⑵在图②中画一个面积为10的正方形；

⑶把图②中的数轴补充完整，再利用圆规在数轴上找出表示 $\sqrt{10}$ 的点

查看试题解析

五、解答题（共4题，共46分）

23. 阅读下面的文字，解答问题：
大家知道 $\sqrt{2}$ 是无理数，而无理数是无限不循环小数，因此 $\sqrt{2}$ 的小数部分我们不可能全部地写出来，于是小明用 $\sqrt{2} - 1$ 来表示 $\sqrt{2}$ 的小数部分，因为 $\sqrt{2}$ 的整数部分是1，将这个数减去其整数部分，差就是小数部分.又例如： $∵ \sqrt{4} < \sqrt{7} < \sqrt{9}$ ，即 $2 < \sqrt{7} < 3 ， ∴ \sqrt{7}$ 的整数部分为2，小数部分为 $(\sqrt{7} - 2)$ .

请解答：

(1)、 $\sqrt{15}$ 的整数部分是，小数部分是.

(2)、已知 $(2 + \sqrt{6})$ 的小数部分为 $a ， (5 - \sqrt{6})$ 的小数部分为 $b$ ，计算 $a + b$ 的值.

查看试题解析
24. 卡塔尔世界杯正在火热进行中，在购买足球赛门票时，设购买门票张数为 a（张），现有两种购买方案：方案一：若单位赞助广告费 10000 元，则该单位购买门票的价格为60元（总费用＝广告赞助费+门票费）．方案二：若购买的门票数不超过 100 张，每张 100 元，若所购门票超过 100 张，则超出部分按八折计算．解答下列问题：

(1)、方案一中，用含 a 的代数式来表示总费用为．方案二中，当购买的门票数 a 不超过 100 张时，用含 x 的代数式来表示总费用为 .当所购门票数 a 超过 100 张时，用含 x 的代数式来表示总费用为．

(2)、甲、乙两单位分别采用方案一、方案二购买本次足球赛门票，合计 700 张，花去的总费用计 58000元，求甲、乙两单位各购买门票多少张？

查看试题解析
25. 如图1，将一副直角三角板的两顶点重合叠放于点 $O$ ，其中一个三角板的顶点 $C$ 落在另一个三角板的边 $O A$ 上.已知 $∠ A B O = ∠ D C O = 90^{\circ}$ ， $∠ A O B = 45^{\circ}$ ， $∠ C O D = 60^{\circ}$ ，作 $∠ A O D$ 的平分线交边 $C D$ 于点 $E$ .

(1)、求 $∠ B O E$ 的度数；

(2)、如图2，若点 $C$ 不落在边 $O A$ 上，当 $∠ C O E = 15^{\circ}$ 时，求 $∠ B O D$ 的度数.

查看试题解析
26. 在数轴上，对于不重合的三点A ， B ， C ，给出如下定义：
若点C到点A的距离是点C到点B的距离的2倍，我们就把点C叫做【A ， B】的和谐点．

例如：图中，点A表示的数为﹣1，点B表示的数为2．表示数1的点C到点A的距离是2，到点B的距离是1．那么点C是【A ， B】的和谐点；又如，表示数0的点D到点A的距离是1，到点B的距离是2，那么点D就不是【A ， B】的和谐点，但点D是【B ， A】的和谐点．

(1)、当点A表示的数为﹣4，点B表示的数为8时，
①若点C表示的数为4，则点C（填“是”或“不是”）【A ， B】的和谐点；

②若点D是【B ， A】的和谐点，则点D表示的数是；

(2)、若A ， B在数轴上表示的数分别为﹣2和4，现有一点C从点B出发，以每秒1个单位长度的速度向数轴负半轴方向运动，当点C到达点A时停止，问点C运动多少秒时，C ， A ， B中恰有一个点为其余两点的和谐点？

查看试题解析