2022-2023学年苏科版数学七年级上学期期末练习卷2
试卷更新日期:2022-12-31 类型:期末考试
一、单选题(每题2分,共16分)
-
1. 把 , , , , 这五个数填入下列圆中,使行、列三个数的和相等,其中错误的是( )A、
 B、
B、 C、
C、 D、
D、 2. 2021年温州达到758500000000元,将该数值用科学记数法表示( )A、 B、 C、 D、3. 一个正方体的表面展开图如图所示,六个面上各有一字,连起来的意思是“全面落实双减”,把它折成正方体后,与“全”相对的字是( )
2. 2021年温州达到758500000000元,将该数值用科学记数法表示( )A、 B、 C、 D、3. 一个正方体的表面展开图如图所示,六个面上各有一字,连起来的意思是“全面落实双减”,把它折成正方体后,与“全”相对的字是( ) A、双 B、减 C、落 D、面4. 如图,点A,O,B在一条直线上,OE⊥AB于点O,如果∠1与∠2互余,那么图中相等的角有( )
A、双 B、减 C、落 D、面4. 如图,点A,O,B在一条直线上,OE⊥AB于点O,如果∠1与∠2互余,那么图中相等的角有( ) A、6对 B、5对 C、4对 D、3对5. 一架飞机在A,B两城市间飞行,顺风要5.5h,逆风要6h,风速为24km/h,求A,B两城市间的距离为x的方程是( )A、 B、 C、 D、6. 下列各式中不能表示图中阴影部分面积的是( )
A、6对 B、5对 C、4对 D、3对5. 一架飞机在A,B两城市间飞行,顺风要5.5h,逆风要6h,风速为24km/h,求A,B两城市间的距离为x的方程是( )A、 B、 C、 D、6. 下列各式中不能表示图中阴影部分面积的是( ) A、 B、 C、 D、7. 设三个互不相等的有理数,既可以表示成1、m+n、m的形式,又可以表示成0、 、n的形式,则m2021+n2021的值为( )A、0 B、1 C、-1 D、28. n个球队进行单循环比赛(参加比赛的每一个队都与其他所有队各赛一场),总的比赛场数是( )A、 B、 C、 D、
A、 B、 C、 D、7. 设三个互不相等的有理数,既可以表示成1、m+n、m的形式,又可以表示成0、 、n的形式,则m2021+n2021的值为( )A、0 B、1 C、-1 D、28. n个球队进行单循环比赛(参加比赛的每一个队都与其他所有队各赛一场),总的比赛场数是( )A、 B、 C、 D、二、填空题(每题2分,共20分)
-
9. 有理数-6的相反数是 .10. 七年级(1)班第一次数学测试平均成绩是88分,小皓考了93分,记作“+5分”,那么小张考了81分,记作 .11. 单项式的系数是 .12. 若x=﹣1是关于x的方程2x+5a=3的解,则a的值 .13. 计算: .14. 一个角为 , 则它的余角度数为 .15. 若单项式与单项式的和仍然是一个单项式A,则A=16. 如图在一条可以折叠的数轴上,点表示的数分别是 , 若以点为折点,将此数轴向右对折,若点落在点右边,且两点相距1单位长,则点表示的数是 .
 17. 如图,在∠AOB的内部有3条射线OC、OD、OE,若∠AOC=70°,∠BOE= ∠BOC,∠BOD= ∠AOB,则∠DOE=°.(用含n的代数式表示)
17. 如图,在∠AOB的内部有3条射线OC、OD、OE,若∠AOC=70°,∠BOE= ∠BOC,∠BOD= ∠AOB,则∠DOE=°.(用含n的代数式表示)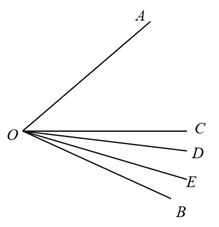 18. 已知关于x的方程 的解是 ,则 的值为.
18. 已知关于x的方程 的解是 ,则 的值为.三、解答题(共8题,共4分)
-
19. 计算:(1)、;(2)、;(3)、 .20. 解下列方程:(1)、4x-8=3(2-x).(2)、 .21. 化简:(1)、;(2)、先化简,再求值:其中 , .22. 如图1,是由8个大小相同的小正方体组合成的简单几何体,该几何体从正面看如图所示.
 (1)、请在方格纸中分别画出从左面看和上面看的形状图;(2)、求该几何体的表面积.(每个小正方体棱长为1个单位)23. 我们规定,如果两个角的差是一个直角,那么这两个角互为足角.其中的一个角叫做另一个角的足角.
(1)、请在方格纸中分别画出从左面看和上面看的形状图;(2)、求该几何体的表面积.(每个小正方体棱长为1个单位)23. 我们规定,如果两个角的差是一个直角,那么这两个角互为足角.其中的一个角叫做另一个角的足角. (1)、如图,直线经过点O,OE平分 , . 请直接写出图中的足角;(2)、如果一个角的足角等于这个角的补角,求这个角的度数.24. 区域需要将一段长为120米的绿化带进行整修,整修任务由甲、乙两个工程队先后接力共同完成.已知甲工程队每天可以整修8米,乙工程队每天可以整修6米,两个工程队共用了18天,问甲、乙两个工程队整修绿化带分别参加了几天?25. 卡塔尔世界杯正在火热进行中,在购买足球赛门票时,设购买门票张数为 a(张),现有两种购买方案:方案一:若单位赞助广告费 10000 元,则该单位购买门票的价格为60元(总费用=广告赞助费+门票费).方案二:若购买的门票数不超过 100 张,每张 100 元,若所购门票超过 100 张,则超出部分按八折计算. 解答下列问题:(1)、方案一中,用含 a 的代数式来表示总费用为 . 方案二中,当购买的门票数 a 不超过 100 张时,用含 x 的代数式来表示总费用为 .当所购门票数 a 超过 100 张时,用含 x 的代数式来表示总费用为 .(2)、甲、乙两单位分别采用方案一、方案二购买本次足球赛门票,合计 700 张,花去的总费用计 58000元,求甲、乙两单位各购买门票多少张?26. 如图,数轴上点A、B、C对应的数分别为a、b、c,且a、b、c使得 与 互为同类项.动点P从A点出发沿数轴以每秒5个单位的速度向右运动,当点P运动到点C之后立即以原速沿数轴向左运动,动点P从A点出发的同时动点Q从B点出发沿数轴以每秒1个单位的速度向右运动.设运动的时间为t秒,
(1)、如图,直线经过点O,OE平分 , . 请直接写出图中的足角;(2)、如果一个角的足角等于这个角的补角,求这个角的度数.24. 区域需要将一段长为120米的绿化带进行整修,整修任务由甲、乙两个工程队先后接力共同完成.已知甲工程队每天可以整修8米,乙工程队每天可以整修6米,两个工程队共用了18天,问甲、乙两个工程队整修绿化带分别参加了几天?25. 卡塔尔世界杯正在火热进行中,在购买足球赛门票时,设购买门票张数为 a(张),现有两种购买方案:方案一:若单位赞助广告费 10000 元,则该单位购买门票的价格为60元(总费用=广告赞助费+门票费).方案二:若购买的门票数不超过 100 张,每张 100 元,若所购门票超过 100 张,则超出部分按八折计算. 解答下列问题:(1)、方案一中,用含 a 的代数式来表示总费用为 . 方案二中,当购买的门票数 a 不超过 100 张时,用含 x 的代数式来表示总费用为 .当所购门票数 a 超过 100 张时,用含 x 的代数式来表示总费用为 .(2)、甲、乙两单位分别采用方案一、方案二购买本次足球赛门票,合计 700 张,花去的总费用计 58000元,求甲、乙两单位各购买门票多少张?26. 如图,数轴上点A、B、C对应的数分别为a、b、c,且a、b、c使得 与 互为同类项.动点P从A点出发沿数轴以每秒5个单位的速度向右运动,当点P运动到点C之后立即以原速沿数轴向左运动,动点P从A点出发的同时动点Q从B点出发沿数轴以每秒1个单位的速度向右运动.设运动的时间为t秒, (1)、填空: , , Q点在数轴上所表示的数为(用t的代数式表示).(2)、在整个运动过程中,t取何值时 ?(3)、若动点P从A点出发的同时动点M也从点C出发沿数轴向左运动,运动速度为每秒2个单位长度,是否存在正数n使得 在一段时间内为定值,如果不存在,说明理由;如果存在,求出正数n.
(1)、填空: , , Q点在数轴上所表示的数为(用t的代数式表示).(2)、在整个运动过程中,t取何值时 ?(3)、若动点P从A点出发的同时动点M也从点C出发沿数轴向左运动,运动速度为每秒2个单位长度,是否存在正数n使得 在一段时间内为定值,如果不存在,说明理由;如果存在,求出正数n.