2022-2023学年苏科版数学八年级上学期期末练习卷3
试卷更新日期:2022-12-31 类型:期末考试
一、单选题(每题2分,共16分)
-
1. 下列各组数中是勾股数的是( )A、4,5, 6 B、1.5,2, 2.5 C、11,60, 61 D、1, ,22. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 如图,用三角尺可按下面方法画角平分线:在已知的∠AOB 的两边上分别取点M、N,使OM=ON,再分别过点M、N作OA、OB的垂线,交点为P,画射线OP.可证得△POM≌△PON,OP平分∠AOB.以上依画法证明△POM≌△PON根据的是( )
3. 如图,用三角尺可按下面方法画角平分线:在已知的∠AOB 的两边上分别取点M、N,使OM=ON,再分别过点M、N作OA、OB的垂线,交点为P,画射线OP.可证得△POM≌△PON,OP平分∠AOB.以上依画法证明△POM≌△PON根据的是( ) A、SSS B、SAS C、AAS D、HL4. 若点A(-2,n)在x轴上,则点B(n-1,n+1)在( ).A、第一象限 B、第二象限 C、第三象限 D、第四象限5. 如图,台阶阶梯每一层高20cm,宽30cm,长50cm,一只蚂蚁从A点爬到B点,最短路程是( )
A、SSS B、SAS C、AAS D、HL4. 若点A(-2,n)在x轴上,则点B(n-1,n+1)在( ).A、第一象限 B、第二象限 C、第三象限 D、第四象限5. 如图,台阶阶梯每一层高20cm,宽30cm,长50cm,一只蚂蚁从A点爬到B点,最短路程是( ) A、 B、 C、120 D、1306. 如图,在正方形ABCD中,E是AB上一点,BE=2,AE=3BE,P是AC上一动点,则PB+PE的最小值为( ).
A、 B、 C、120 D、1306. 如图,在正方形ABCD中,E是AB上一点,BE=2,AE=3BE,P是AC上一动点,则PB+PE的最小值为( ).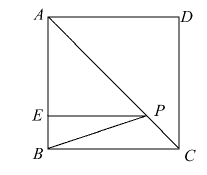 A、8 B、8 C、10 D、7. 在同一直角坐标系中,一次函数y=(k﹣2)x+k的图象与正比例函数y=kx图象的位置可能是( )A、
A、8 B、8 C、10 D、7. 在同一直角坐标系中,一次函数y=(k﹣2)x+k的图象与正比例函数y=kx图象的位置可能是( )A、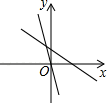 B、
B、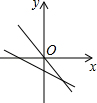 C、
C、 D、
D、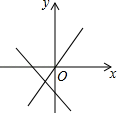 8. 如图,在中, , 是边上的两点,且 , , 设 , , 则与之间的关系式为( )
8. 如图,在中, , 是边上的两点,且 , , 设 , , 则与之间的关系式为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每题2分,共20分)
-
9. 当x= 时, 值为0。10. 如图,数轴上点A表示数-1,点B表示数1,过点B作BC垂直于数轴,若BC=1,以A为圆心,AC为半径作圆弧交数轴的正半轴于点P,则点P所表示的数是 .
 11. 为了比较 +1与 的大小,可以构造如图所示的图形进行推算,其中∠C=90°,BC=4,D在BC上且BD=AC=1.通过计算可得 +1 .(填“>”或“<”或“=”)
11. 为了比较 +1与 的大小,可以构造如图所示的图形进行推算,其中∠C=90°,BC=4,D在BC上且BD=AC=1.通过计算可得 +1 .(填“>”或“<”或“=”) 12. 如图,ABC中,AC=BC,且点D在ABC外,D在AC的垂直平分线上,连接BD, 若∠DBC=30°∠ACD=13°,则∠A=°
12. 如图,ABC中,AC=BC,且点D在ABC外,D在AC的垂直平分线上,连接BD, 若∠DBC=30°∠ACD=13°,则∠A=° 13. 把直线y= x+1向右平移个单位可得到直线y= x-2.14. 如图,函数 与 的图象交于 .则不等式 的解集为 .
13. 把直线y= x+1向右平移个单位可得到直线y= x-2.14. 如图,函数 与 的图象交于 .则不等式 的解集为 . 15. 一条笔直的公路上依次有A,B,C三地,甲,乙两人同时从A地出发,甲先使用共享单车,经过B地到达停车点C地后再步行返回B地,此时直接步行的乙也恰好到达B地.已知两人步行速度相同,两人离起点A的距离y(米)关于时间x(分)的函数关系如图,则 .
15. 一条笔直的公路上依次有A,B,C三地,甲,乙两人同时从A地出发,甲先使用共享单车,经过B地到达停车点C地后再步行返回B地,此时直接步行的乙也恰好到达B地.已知两人步行速度相同,两人离起点A的距离y(米)关于时间x(分)的函数关系如图,则 . 16. 如图,已知正方形ABOC的顶点B(2,1),则顶点C的坐标为 .
16. 如图,已知正方形ABOC的顶点B(2,1),则顶点C的坐标为 .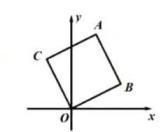 17. 已知一次函数 为常数),当x<2时,y>0,则 的取值范围为 .18. 如图,正方形ABCD边长为2,F为对角线AC上的一个动点,过C作AC的垂线并截取 , 连结EF,周长的最小值为 .
17. 已知一次函数 为常数),当x<2时,y>0,则 的取值范围为 .18. 如图,正方形ABCD边长为2,F为对角线AC上的一个动点,过C作AC的垂线并截取 , 连结EF,周长的最小值为 .
三、解答题(共9题,共64分)
-
19. 求下列各式中x的值:(1)、2x2-32=0;(2)、(x+4)3+64=0.20. 如图,在中,是对角线,⊥ , ⊥ , 垂足分别为E、F.求证:△≌△ .
 21. 作图题(1)、如图所示,画出△ABC关于直线MN的轴对称图形.
21. 作图题(1)、如图所示,画出△ABC关于直线MN的轴对称图形. (2)、已知:∠AOB和两点M、N,求作:一点P,使点P到∠AOB两边的距离相等,且PM=PN.(尺规作图,保留作图痕迹)
(2)、已知:∠AOB和两点M、N,求作:一点P,使点P到∠AOB两边的距离相等,且PM=PN.(尺规作图,保留作图痕迹) 22. 明朝数学家程大位在他的著作《算法统宗》中写了一首计算秋千绳索长度的词《西江月》:“平地秋千未起,踏板一尺离地,送行二步恰竿齐,五尺板高离地…”翻译成现代文为:如图,秋千静止的时候,踏板离地高一尺(尺),将它往前推进两步(尺),此时踏板升高离地五尺(尺),求秋千绳索(或)的长度.
22. 明朝数学家程大位在他的著作《算法统宗》中写了一首计算秋千绳索长度的词《西江月》:“平地秋千未起,踏板一尺离地,送行二步恰竿齐,五尺板高离地…”翻译成现代文为:如图,秋千静止的时候,踏板离地高一尺(尺),将它往前推进两步(尺),此时踏板升高离地五尺(尺),求秋千绳索(或)的长度. 23. 已知y是x的一次函数,且当 时, ;当 时, .(1)、求这个一次函数的解析式;(2)、当 时,求函数y的值;(3)、当 时,求自变量x的取值范围.24. 等腰Rt△ABC,点D为斜边AB上的中点,点E在线段BD上,连结CD,CE,作AH⊥CE,垂足为H,交CD于点G,AH的延长线交BC于点F.
23. 已知y是x的一次函数,且当 时, ;当 时, .(1)、求这个一次函数的解析式;(2)、当 时,求函数y的值;(3)、当 时,求自变量x的取值范围.24. 等腰Rt△ABC,点D为斜边AB上的中点,点E在线段BD上,连结CD,CE,作AH⊥CE,垂足为H,交CD于点G,AH的延长线交BC于点F.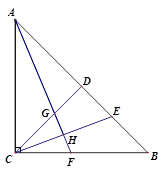 (1)、求证:△ADG≌△CDE.(2)、若点H恰好为CE的中点,求证:∠CGF=∠CFG.25. 如图,直线l:y=x+b过点A(﹣3,0),与y轴交于点B,∠OAB的平分线交y轴于点C,过点C作直线AB的垂线,交x轴于点E,垂足是点D.
(1)、求证:△ADG≌△CDE.(2)、若点H恰好为CE的中点,求证:∠CGF=∠CFG.25. 如图,直线l:y=x+b过点A(﹣3,0),与y轴交于点B,∠OAB的平分线交y轴于点C,过点C作直线AB的垂线,交x轴于点E,垂足是点D. (1)、求点B和点C的坐标;(2)、求直线DE的函数关系式;(3)、设点P是y轴上一动点,当PA+PD的值最小时,请直接写出点P的坐标.26. 甲、乙两地间的直线公路长为 千米.一辆轿车和一辆货车分别沿该公路从甲、乙两地以各自的速度匀速相向而行,货车比轿车早出发 小时,途中轿车出现了故障,停下维修,货车仍继续行驶. 小时后轿车故障被排除,此时接到通知,轿车立刻掉头按原路原速返回甲地(接到通知及掉头时间不计).最后两车同时到达甲地,已知两车距各自出发地的距离 (千米)与轿车所用的时间 (小时)的关系如图所示,请结合图象解答下列问题:
(1)、求点B和点C的坐标;(2)、求直线DE的函数关系式;(3)、设点P是y轴上一动点,当PA+PD的值最小时,请直接写出点P的坐标.26. 甲、乙两地间的直线公路长为 千米.一辆轿车和一辆货车分别沿该公路从甲、乙两地以各自的速度匀速相向而行,货车比轿车早出发 小时,途中轿车出现了故障,停下维修,货车仍继续行驶. 小时后轿车故障被排除,此时接到通知,轿车立刻掉头按原路原速返回甲地(接到通知及掉头时间不计).最后两车同时到达甲地,已知两车距各自出发地的距离 (千米)与轿车所用的时间 (小时)的关系如图所示,请结合图象解答下列问题: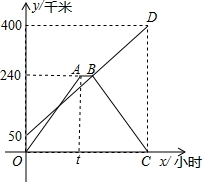 (1)、货车的速度是千米/小时;轿车的速度是千米/小时; 值为.(2)、求轿车距其出发地的距离 (千米)与所用时间 (小时)之间的函数关系式并写出自变量 的取值范围;(3)、请直接写出货车出发多长时间两车相距 千米.27. 通过对下面数学模型的研究学习,解决下列问题:
(1)、货车的速度是千米/小时;轿车的速度是千米/小时; 值为.(2)、求轿车距其出发地的距离 (千米)与所用时间 (小时)之间的函数关系式并写出自变量 的取值范围;(3)、请直接写出货车出发多长时间两车相距 千米.27. 通过对下面数学模型的研究学习,解决下列问题: (1)、【模型呈现】
(1)、【模型呈现】如图1,∠BAD=90°,AB=AD,过点B作BC⊥AC于点C,过点D作DE⊥AC于点E.由∠1+∠2=∠2+∠D=90°,得∠1=∠D.又∠ACB=∠AED=90°,可以推理得到△ABC≌△DAE.进而得到AC= , BC= . 我们把这个数学模型称为“K字”模型或“一线三等角”模型;
(2)、【模型应用】如图2,∠BAD=∠CAE=90°,AB=AD,AC=AE,连接BC,DE,且BC⊥AF于点F,DE与直线AF交于点G.求证:点G是DE的中点;
(3)、如图3,在平面直角坐标系xOy中,点A的坐标为(2,6),点B为平面内任一点.若△AOB是以OA为斜边的等腰直角三角形,请直接写出点B的坐标.