2022-2023学年苏科版九年级上学期数学期末模拟试卷3
试卷更新日期:2022-12-31 类型:期末考试
一、单选题(每题2分,共12分)
-
1. 菱形ABCD的一条对角线长为6,边AB的长为方程y2﹣7y+10=0的一个根,则菱形ABCD的周长为( )A、8 B、20 C、8或20 D、102. 若抛物线与x轴只有一个交点,则k的值为( )A、-1 B、0 C、1 D、23. 为了调查某小区居民的用水情况,随机抽查了若干户家庭的月用水量,结果如表:
月用水量/吨
3
4
6
10
12
户数/户
2
4
3
2
1
则关于这若干户家庭的用水量,下列说法错误的是( )
A、众数是4 B、平均数是7 C、调查了12户家庭的月用水量 D、中位数是54. 如图,在Rt△ABC中,∠BAC=90°,AD是斜边BC上的高,其中正确的命题是( )①AB2=BD•BC;②AD2=BD•BC;③AC2=CD•CB;④AB•AC=AD•CB
 A、①②③ B、①②③④ C、①④ D、①③④5. 二次函数 的部分图象如图所示,当 时,函数值 的取值范围是( )
A、①②③ B、①②③④ C、①④ D、①③④5. 二次函数 的部分图象如图所示,当 时,函数值 的取值范围是( ) A、 B、 C、 D、6. 如图,在矩形ABCD中,AB=8,AD=6,点M为对角线AC上的一个动点(不与端点A,C重合),过点M作ME⊥AD,MF⊥DC,垂足分别为E,F,则四边形EMFD面积的最大值为( )
A、 B、 C、 D、6. 如图,在矩形ABCD中,AB=8,AD=6,点M为对角线AC上的一个动点(不与端点A,C重合),过点M作ME⊥AD,MF⊥DC,垂足分别为E,F,则四边形EMFD面积的最大值为( )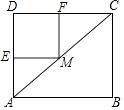 A、6 B、12 C、18 D、24
A、6 B、12 C、18 D、24二、填空题(每题2分,共20分)
-
7. 若 ,则 的值为.8. 将二次函数的图象沿x轴向右平移2个单位长度,得到的函数解析式是.9. 方程2x2-3x-1=0,则+=.10. 如图,测量小玻璃管口径的量具ABC上,AB的长为10毫米,AC被分为60等份,如果小管口中DE正好对着量具上20份处(DE∥AB),那么小管口径DE的长是毫米.
 11. 如图, 是 的直径,点 在 上,点 在 上, , 于 .若 ,则 为 .
11. 如图, 是 的直径,点 在 上,点 在 上, , 于 .若 ,则 为 . 12. 如图,正六边形和正五边形内接于 , 且有公共顶点A,则的度数为度.
12. 如图,正六边形和正五边形内接于 , 且有公共顶点A,则的度数为度.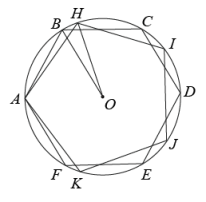 13. 如图,中,E是边AD的中点,BE交对角线AC于点F,那么S△AFB :S四边形FEDC的值为
13. 如图,中,E是边AD的中点,BE交对角线AC于点F,那么S△AFB :S四边形FEDC的值为 14. 如图,将矩形ABCD沿直线AC折叠,点B落在点E处,连接DE,BE,若△ABE为等边三角形,且S△CDE= ,则CD的长为 .
14. 如图,将矩形ABCD沿直线AC折叠,点B落在点E处,连接DE,BE,若△ABE为等边三角形,且S△CDE= ,则CD的长为 . 15. 在矩形ABCD中,∠ABC的平分线交边AD于点E,∠BED的平分线交直线CD于点F.若AB=3,CF=1,则BC=.16. 二次函数 图象 轴上方的部分沿 轴翻折到 轴下方,图象的其余部分保持不变,翻折后的图象与原图象 轴下方的部分组成一个“ ”形状的新图象,若直线 与该新图象有两个公共点,则 的取值范围为.
15. 在矩形ABCD中,∠ABC的平分线交边AD于点E,∠BED的平分线交直线CD于点F.若AB=3,CF=1,则BC=.16. 二次函数 图象 轴上方的部分沿 轴翻折到 轴下方,图象的其余部分保持不变,翻折后的图象与原图象 轴下方的部分组成一个“ ”形状的新图象,若直线 与该新图象有两个公共点,则 的取值范围为.三、解答题(共11题,共88分)
-
17. 某社区准备在甲、乙两位射箭爱好者中选出一人参加集训,两人各射了 箭,他们的总成绩(单位:环)相同,小宇根据他们的成绩计算了甲成绩的平均数和方差(见小宇的作业).

第 次
第 次
第 次
第 次
第 次
甲成绩
乙成绩
(1)、求a和乙的方差 ;(2)、请你从平均数和方差的角度分析,谁将被选中.18. 羽毛球团体赛小组赛比赛规则:两队之间进行五局比赛,其中三局单打.两局双打,五局比赛必须全部打完,赢得三局及以上的队获胜.假如甲、乙两队每局获胜的机会相同.(1)、若前四局双方战成2:2,那么甲队最终获胜的概率是多少?(2)、现甲队在前两局比赛中已取得2:0的领先,那么甲队最终获胜的概率是多少?(用“列表”或“画树状图”给出分析过程)19.(1)、用公式法解方程2x2-2x-1=0;(2)、用配方法解方程2x2-6x-1=0.20. 为抗旱保丰收,某地政府制定农户投资购买抗旱设备的补贴办法,其中购买Ⅰ型、Ⅱ型抗旱设备所投资的金额与政府补贴的额度存在下表所示的函数对应关系.型号
金额
Ⅰ型设备
Ⅱ型设备
投资金额x(万元)
x
5
x
2
4
补贴金额y(万元)
2
(1)、分别求出和的函数关系式;(2)、有一农户同时对Ⅰ型、Ⅱ型两种设备共投资10万元进行购买,请你设计一个能获得最大补贴金额的方案,并求出按此方案能获得的最大补贴金额.21. 如图, 的三个顶点的坐标分别为 .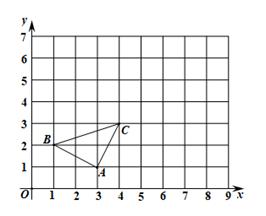 (1)、以原点O为位似中心,在第一象限内将 放大为原来的2倍得到 ,作出 ,写出 的坐标;(2)、P为第一象限的整点(横纵坐标都是整数的点), 平分 ,直接写出点P的坐标.22. 如图,四边形ABCD内接于 为 的直径,D为弧AC的中点,过点D作 ,交BC的延长线于点E.
(1)、以原点O为位似中心,在第一象限内将 放大为原来的2倍得到 ,作出 ,写出 的坐标;(2)、P为第一象限的整点(横纵坐标都是整数的点), 平分 ,直接写出点P的坐标.22. 如图,四边形ABCD内接于 为 的直径,D为弧AC的中点,过点D作 ,交BC的延长线于点E. (1)、判断DE与 的位置关系,并说明理由;(2)、若 的半径为5,BC=6, 求CE的长.23. 在 中, , 垂直平分 ,分别交 于点 .
(1)、判断DE与 的位置关系,并说明理由;(2)、若 的半径为5,BC=6, 求CE的长.23. 在 中, , 垂直平分 ,分别交 于点 . (1)、求证: ;(2)、求证: .24. 如图, 是 的直径, ,点 是劣弧 上一点,过点 作 的切线 ,交 的延长线于点 , 交 于点 .
(1)、求证: ;(2)、求证: .24. 如图, 是 的直径, ,点 是劣弧 上一点,过点 作 的切线 ,交 的延长线于点 , 交 于点 . (1)、求证: ;(2)、若 , ,过点 作 交 于点 ,求 的长.25. 定义:在平面直角坐标系 中,点 为图形 上一点,点 为图形 上一点.若存在 ,则称图形 与图形 关于原点 “平衡”.(1)、如图,已知⊙ 是以 为圆心, 为半径的圆,点 , , .
(1)、求证: ;(2)、若 , ,过点 作 交 于点 ,求 的长.25. 定义:在平面直角坐标系 中,点 为图形 上一点,点 为图形 上一点.若存在 ,则称图形 与图形 关于原点 “平衡”.(1)、如图,已知⊙ 是以 为圆心, 为半径的圆,点 , , .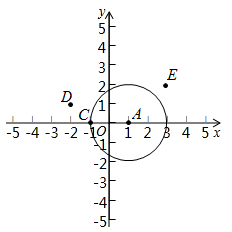
①在点 , , 中,与⊙ 关于原点 “平衡”的点是;
②点 为直线 上一点,若点 与⊙ 关于原点 “平衡”,点 的横坐标的取值范围为:;
(2)、如图,已知图形 是以原点 为中心,边长为 的正方形.⊙ 的圆心在 轴上,半径为 .若⊙ 与图形 关于原点 “平衡”,请直接写出圆心 的横坐标的取值范围. 26. 已知关于x的一元二次方程mx2+(3m+1)x+3=0.
26. 已知关于x的一元二次方程mx2+(3m+1)x+3=0. (1)、求证:该方程有两个实数根;(2)、如果抛物线y=mx2+(3m+1)x+3与x轴交于A、B两个整数点(点A在点B左侧),且m为正整数,求此抛物线的表达式;(3)、在(2)的条件下,抛物线y=mx2+(3m+1)x+3与y轴交于点C,点B关于y轴的对称点为D,设此抛物线在-3≤x≤- 之间的部分为图象G,如果图象G向右平移n(n>0)个单位长度后与直线CD有公共点,求n的取值范围.27. 如图1, 是 的高, .
(1)、求证:该方程有两个实数根;(2)、如果抛物线y=mx2+(3m+1)x+3与x轴交于A、B两个整数点(点A在点B左侧),且m为正整数,求此抛物线的表达式;(3)、在(2)的条件下,抛物线y=mx2+(3m+1)x+3与y轴交于点C,点B关于y轴的对称点为D,设此抛物线在-3≤x≤- 之间的部分为图象G,如果图象G向右平移n(n>0)个单位长度后与直线CD有公共点,求n的取值范围.27. 如图1, 是 的高, .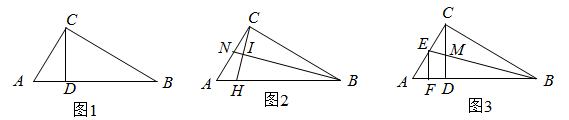 (1)、求证: .(2)、如图2, 是 的中线, 于点I交 于H点,若 ,求 的值.(3)、如图3,M是 的中点, 交 于E, 于F.若 , ,直接写出 的值.
(1)、求证: .(2)、如图2, 是 的中线, 于点I交 于H点,若 ,求 的值.(3)、如图3,M是 的中点, 交 于E, 于F.若 , ,直接写出 的值.