浙教版备考2023年中考数学一轮复习59.三角形的中位线定理
试卷更新日期:2022-12-31 类型:一轮复习
一、单选题(每题3分,共30分)
-
1. 如图,在中, , 点D、E分别是直角边AC、BC的中点,连接DE,则度数是( )
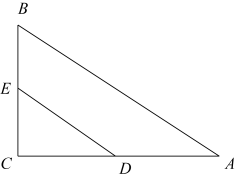 A、70° B、60° C、30° D、20°2. 如图,正方形ABCD的面积为3,点E在边CD上, 且CE = 1,∠ABE的平分线交AD于点F,点M,N分别是BE,BF的中点,则MN的长为( )
A、70° B、60° C、30° D、20°2. 如图,正方形ABCD的面积为3,点E在边CD上, 且CE = 1,∠ABE的平分线交AD于点F,点M,N分别是BE,BF的中点,则MN的长为( )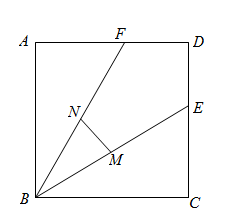 A、 B、 C、 D、3. 如图,是的中线, , 分别是 , 的中点,连接EF.若 , 则的长为( )
A、 B、 C、 D、3. 如图,是的中线, , 分别是 , 的中点,连接EF.若 , 则的长为( ) A、 B、2 C、 D、44. 如图,四边形是菱形, , 点是中点,是对角线上一点,且 , 则的值是( )
A、 B、2 C、 D、44. 如图,四边形是菱形, , 点是中点,是对角线上一点,且 , 则的值是( )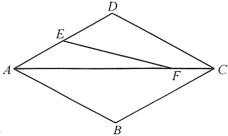 A、3 B、 C、 D、5. 在中, , , , 点 , , 分别为边 , , 的中点,则的周长为( )A、9 B、12 C、14 D、166. 如图,在 △ABC中,D、E分别为线段BC、BA的中点,设△ABC的面积为S1 , △EBD的面积为S2 . 则 =( )
A、3 B、 C、 D、5. 在中, , , , 点 , , 分别为边 , , 的中点,则的周长为( )A、9 B、12 C、14 D、166. 如图,在 △ABC中,D、E分别为线段BC、BA的中点,设△ABC的面积为S1 , △EBD的面积为S2 . 则 =( ) A、 B、 C、 D、7. 如图,点I为的内心,连接并延长交的外接圆于点D,点E为弦的中点,连接 , , , 当 , , 时,的长为( )
A、 B、 C、 D、7. 如图,点I为的内心,连接并延长交的外接圆于点D,点E为弦的中点,连接 , , , 当 , , 时,的长为( )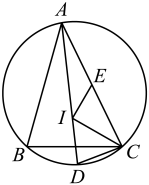 A、5 B、4.5 C、4 D、3.58. 如图,G为的重心,点D在延长线上,且 , 过D、G的直线交于点E,则为( )
A、5 B、4.5 C、4 D、3.58. 如图,G为的重心,点D在延长线上,且 , 过D、G的直线交于点E,则为( ) A、 B、 C、 D、9. 如图,C是以AB为直径的半圆O上一点,连结AC,BC,分别以AC,BC为边向外作正方形ACDE与BCFG,点M,N,P,Q分别是DE,FG,弧AC,弧BC的中点.若MP+NQ=14,AC+BC=18,则AB的长是( )
A、 B、 C、 D、9. 如图,C是以AB为直径的半圆O上一点,连结AC,BC,分别以AC,BC为边向外作正方形ACDE与BCFG,点M,N,P,Q分别是DE,FG,弧AC,弧BC的中点.若MP+NQ=14,AC+BC=18,则AB的长是( ) A、 B、 C、13 D、1610. 如图,在中, , 是的中点,延长至点 , 使 , 连接 , 为中点,连接若 , , 则的长为( )
A、 B、 C、13 D、1610. 如图,在中, , 是的中点,延长至点 , 使 , 连接 , 为中点,连接若 , , 则的长为( )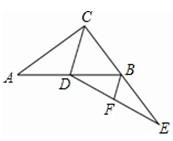 A、5 B、4 C、6 D、8
A、5 B、4 C、6 D、8二、填空题(每题4分,共24分)
-
11. 如图,如果要测量池塘两端A,B的距离,可以在池塘外取一点C,连接AC,BC,点D,E分别是AC,BC的中点,测得DE的长为25米,则AB的长为 米.
 12. 如图,在和中, , 、、分别为、、的中点,若 , 则 .
12. 如图,在和中, , 、、分别为、、的中点,若 , 则 . 13. 如图,中, , , 点 , 分别是 , 的中点,点在上,且 , 则EF= .
13. 如图,中, , , 点 , 分别是 , 的中点,点在上,且 , 则EF= .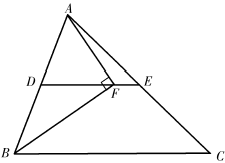 14. 如图,在矩形中,对角线 , 相交于点 , 点是边的中点,点在对角线上,且 , 连接 . 若 , 则 .
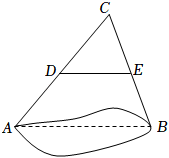
14. 如图,在矩形中,对角线 , 相交于点 , 点是边的中点,点在对角线上,且 , 连接 . 若 , 则 . 15. 如图,在 中, ,点D,E分别是 边上的中点,连接 .如果 , ,那么 的长是m.
15. 如图,在 中, ,点D,E分别是 边上的中点,连接 .如果 , ,那么 的长是m. 16. “做数学”可以帮助我们积累数学活动经验.如图,已知三角形纸片 , 第1次折叠使点落在边上的点处,折痕交于点;第2次折叠使点落在点处,折痕交于点.若 , 则.
16. “做数学”可以帮助我们积累数学活动经验.如图,已知三角形纸片 , 第1次折叠使点落在边上的点处,折痕交于点;第2次折叠使点落在点处,折痕交于点.若 , 则.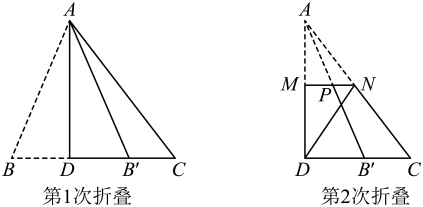
三、解答题(共8题,共66分)
-
17. 如图,是由个边长为1的小正方形网格组成,每个小正方形的顶点称为格点,的三个顶点A,B,C均在格点上,在AB,BC上各取一点D,E,请仅用无刻度的直尺,按下列要求画图.(1)、在图中画线段DE,使线段且;
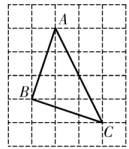 (2)、在图中画线段DE,使线段且.
(2)、在图中画线段DE,使线段且.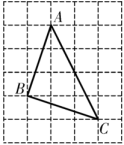 18. 如图,在中,已知 , , 平分 , 于点 , 为中点.求的长.
18. 如图,在中,已知 , , 平分 , 于点 , 为中点.求的长. 19. 三角形三条边上的中线交于一点,这个点叫三角形的重心.如图G是 的重心.求证: .
19. 三角形三条边上的中线交于一点,这个点叫三角形的重心.如图G是 的重心.求证: .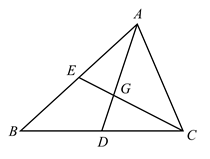 20. 如图,线段DE与AF分别为△ABC的中位线与中线.
20. 如图,线段DE与AF分别为△ABC的中位线与中线.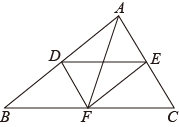 (1)、求证:AF与DE互相平分;(2)、当线段AF与BC满足怎样的数量关系时,四边形ADFE为矩形?请说明理由.21. 如图,在半径为5的扇形AOB中,∠AOB=90°,点C是弧AB上的一个动点(不与点A、B重合)OD⊥BC,OE⊥AC,垂足分别为D、E.
(1)、求证:AF与DE互相平分;(2)、当线段AF与BC满足怎样的数量关系时,四边形ADFE为矩形?请说明理由.21. 如图,在半径为5的扇形AOB中,∠AOB=90°,点C是弧AB上的一个动点(不与点A、B重合)OD⊥BC,OE⊥AC,垂足分别为D、E.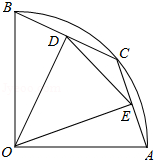 (1)、当BC=6时,求线段OD的长;(2)、在△DOE中是否存在长度保持不变的边?如果存在,请指出并求其长度;如果不存在,请说明理由.22. 如图,在△ABC中,AD是高,E、F分别为AB、AC的中点,连接DE、EF、FD.
(1)、当BC=6时,求线段OD的长;(2)、在△DOE中是否存在长度保持不变的边?如果存在,请指出并求其长度;如果不存在,请说明理由.22. 如图,在△ABC中,AD是高,E、F分别为AB、AC的中点,连接DE、EF、FD. (1)、若AB=14,AC=10,求四边形AEDF的周长;(2)、EF与AD存在怎样的位置关系?证明你的结论.
(1)、若AB=14,AC=10,求四边形AEDF的周长;(2)、EF与AD存在怎样的位置关系?证明你的结论.

