浙教版备考2023年中考数学一轮复习58.平行四边形性质与判定
试卷更新日期:2022-12-31 类型:一轮复习
一、单选题(每题3分,共30分)
-
1. 如图,在 中,一定正确的是( )
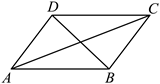 A、 B、 C、 D、2. 依据所标数据,下列一定为平行四边形的是()A、
A、 B、 C、 D、2. 依据所标数据,下列一定为平行四边形的是()A、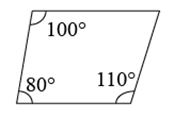 B、
B、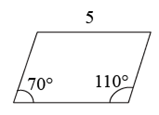 C、
C、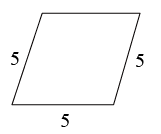 D、
D、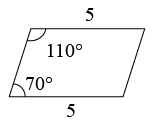 3. 如图,在▱ABCD中,AB=8,点E是AB上一点,AE=3,连接DE,过点C作CF∥DE,交AB的延长线于点F,则BF的长为( )
3. 如图,在▱ABCD中,AB=8,点E是AB上一点,AE=3,连接DE,过点C作CF∥DE,交AB的延长线于点F,则BF的长为( )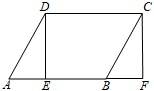 A、5 B、4 C、3 D、24. 如图,在▱ABCD中,已知AB=12,AD=8,∠ABC的平分线BM交CD边于点M,则DM的长为( )
A、5 B、4 C、3 D、24. 如图,在▱ABCD中,已知AB=12,AD=8,∠ABC的平分线BM交CD边于点M,则DM的长为( )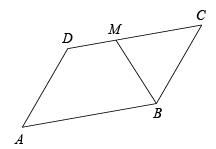 A、2 B、4 C、6 D、85. 如图,在中, , 是上的点,交于点 , 交于点 , 那么四边形的周长是( )
A、2 B、4 C、6 D、85. 如图,在中, , 是上的点,交于点 , 交于点 , 那么四边形的周长是( )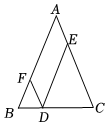 A、5 B、10 C、15 D、206. 如图,剪两张对边平行的纸条,随意交叉叠放在一起,重合部分构成一个四边形 , 其中一张纸条在转动过程中,下列结论一定成立的是( )
A、5 B、10 C、15 D、206. 如图,剪两张对边平行的纸条,随意交叉叠放在一起,重合部分构成一个四边形 , 其中一张纸条在转动过程中,下列结论一定成立的是( )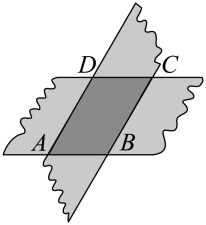 A、四边形周长不变 B、 C、四边形面积不变 D、7. 在▱ABCD中(如图),连接AC,已知∠BAC=40°,∠ACB=80°,则∠BCD=( )
A、四边形周长不变 B、 C、四边形面积不变 D、7. 在▱ABCD中(如图),连接AC,已知∠BAC=40°,∠ACB=80°,则∠BCD=( )
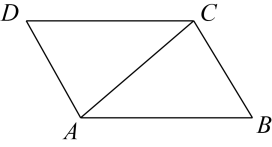 A、80° B、100° C、120° D、140°8. 如图,在 中,点D,E分别是 , 边的中点,点F在 的延长线上.添加一个条件,使得四边形 为平行四边形,则这个条件可以是( )
A、80° B、100° C、120° D、140°8. 如图,在 中,点D,E分别是 , 边的中点,点F在 的延长线上.添加一个条件,使得四边形 为平行四边形,则这个条件可以是( ) A、 B、 C、 D、9. 如图,在▱ABCD中,∠A=60°,AB=2,AD=1,点E,F在▱ABCD的边上,从点A同时出发,分别沿A→B→C和A→D→C的方向以每秒1个单位长度的速度运动,到达点C时停止,线段EF扫过区域的面积记为y,运动时间记为x,能大致反映y与x之间函数关系的图象是( )
A、 B、 C、 D、9. 如图,在▱ABCD中,∠A=60°,AB=2,AD=1,点E,F在▱ABCD的边上,从点A同时出发,分别沿A→B→C和A→D→C的方向以每秒1个单位长度的速度运动,到达点C时停止,线段EF扫过区域的面积记为y,运动时间记为x,能大致反映y与x之间函数关系的图象是( ) A、
A、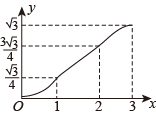 B、
B、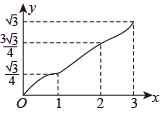 C、
C、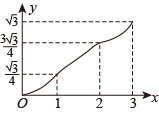 D、
D、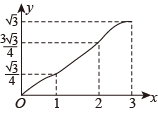 10. 如图, 点P是平行四边形内部一点, 过P分别作和的平行线交平行四边 形的四边于. 连结分别交于M和N. 若四边形四边形 , 且四边形的面积是四边形的3倍. 下列选项正确的是( )
10. 如图, 点P是平行四边形内部一点, 过P分别作和的平行线交平行四边 形的四边于. 连结分别交于M和N. 若四边形四边形 , 且四边形的面积是四边形的3倍. 下列选项正确的是( )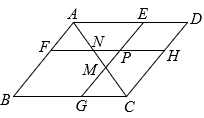 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每题4分,共24分)
-
11. 如图,有一张平行四边形纸片 , , , 将这张纸片折叠,使得点落在边上,点的对应点为点 , 折痕为 , 若点在边上,则长的最小值等于 .
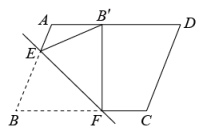 12. 如图,在▱ABCD中,AD=10,对角线AC 与BD相交于点O,AC+BD=22,则△BOC的周长为
12. 如图,在▱ABCD中,AD=10,对角线AC 与BD相交于点O,AC+BD=22,则△BOC的周长为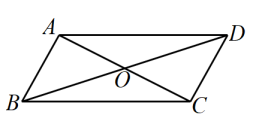 13. 如图,在▱ABCD中,E,F是对角线BD上的两点,要使四边形AFCE是平行四边形,则需添加的一个条件可以是 . (只添加一个条件)
13. 如图,在▱ABCD中,E,F是对角线BD上的两点,要使四边形AFCE是平行四边形,则需添加的一个条件可以是 . (只添加一个条件) 14. 已知:如图,线段AB=6cm,点P是线段AB上的动点,分别以AP、BP为边在AB作等边APC、等边BPD,连接CD,点M是CD的中点,当点P从点A运动到点B时,点M经过的路径的长是cm.
14. 已知:如图,线段AB=6cm,点P是线段AB上的动点,分别以AP、BP为边在AB作等边APC、等边BPD,连接CD,点M是CD的中点,当点P从点A运动到点B时,点M经过的路径的长是cm. 15. 如图在平行四边形ABCD中,E是CD的中点,F是AE的中点,CF交BE于点G,若BE=8,则GE=.
15. 如图在平行四边形ABCD中,E是CD的中点,F是AE的中点,CF交BE于点G,若BE=8,则GE=. 16. 如图,平行四边形ABCD的对角线AC,BD相交于点O, , 点E在线段BO上从点B以1cm/s的速度运动,点F在线段OD上从点O以2cm/s的速度运动.若点E,F同时运动,设运动时间为t秒,当时,四边形AECF是平行四边形.
16. 如图,平行四边形ABCD的对角线AC,BD相交于点O, , 点E在线段BO上从点B以1cm/s的速度运动,点F在线段OD上从点O以2cm/s的速度运动.若点E,F同时运动,设运动时间为t秒,当时,四边形AECF是平行四边形.
三、解答题(共8题,共66分)
-
17. 如图,在四边形中,与交于点 , , , 垂足分别为点 , , 且 , . 求证:四边形是平行四边形.
 18. 如图,在矩形中,F是边上的一点,请在边上求作一点H,连接 , 使得四边形为平行四边形.(保留作图痕迹,不写作法)
18. 如图,在矩形中,F是边上的一点,请在边上求作一点H,连接 , 使得四边形为平行四边形.(保留作图痕迹,不写作法)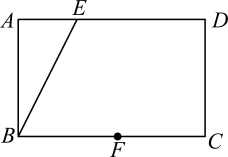 19. 如图,在▱ABCD中,DF平分∠ADC,交AB于点F,BEDF,交AD的延长线于点E.若∠A=40°,求∠ABE的度数.
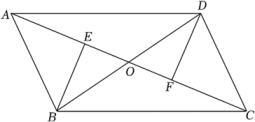
19. 如图,在▱ABCD中,DF平分∠ADC,交AB于点F,BEDF,交AD的延长线于点E.若∠A=40°,求∠ABE的度数.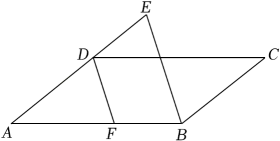 20. 如图,在平行四边形ABCD中,点E、F在对角线BD上,且BE=DF.求证:
20. 如图,在平行四边形ABCD中,点E、F在对角线BD上,且BE=DF.求证: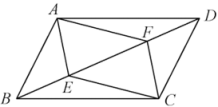 (1)、△ABE≌△CDF;(2)、四边形AECF是平行四边形.21. 已知:如图,在平行四边形ABCD中,E、F为对角线BD上的两点,
(1)、△ABE≌△CDF;(2)、四边形AECF是平行四边形.21. 已知:如图,在平行四边形ABCD中,E、F为对角线BD上的两点, (1)、求证:△AED≌△CFB;(2)、若∠ABC=75°, , , 求平行四边形ABCD的周长.22. 如图,一次函数 与反比例函数 的图象相交于小 ,B两点,分别连接 , .
(1)、求证:△AED≌△CFB;(2)、若∠ABC=75°, , , 求平行四边形ABCD的周长.22. 如图,一次函数 与反比例函数 的图象相交于小 ,B两点,分别连接 , .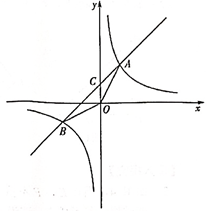 (1)、求这个反比例函数的表达式;(2)、求 的面积:(3)、在平面内是否存在一点P,使以点O,B,A,P为顶点的四边形为平行四边形?若存在,请直接写出点P的坐标;若不存在,请说明理由.23. 如图,二次函数的图象与x轴交于O(O为坐标原点),A两点,且二次函数的最小值为 , 点是其对称轴上一点,y轴上一点.
(1)、求这个反比例函数的表达式;(2)、求 的面积:(3)、在平面内是否存在一点P,使以点O,B,A,P为顶点的四边形为平行四边形?若存在,请直接写出点P的坐标;若不存在,请说明理由.23. 如图,二次函数的图象与x轴交于O(O为坐标原点),A两点,且二次函数的最小值为 , 点是其对称轴上一点,y轴上一点.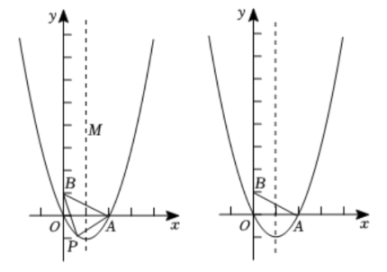 (1)、求二次函数的表达式;(2)、二次函数在第四象限的图象上有一点P,连结 , , 设点P的横坐标为t,的面积为S,求S与t的函数关系式;(3)、在二次函数图象上是否存在点N,使得以A、B、M、N为顶点的四边形是平行四边形?若存在,直接写出所有符合条件的点N的坐标,若不存在,请说明理由.24. 如图,在▱ABCD中,对角线AC,BD相交于点O,OA=5cm,E,F为直线BD上的两个动点(点E、F始终在▱ABCD的外面),连接AE、CE、CF、AF.
(1)、求二次函数的表达式;(2)、二次函数在第四象限的图象上有一点P,连结 , , 设点P的横坐标为t,的面积为S,求S与t的函数关系式;(3)、在二次函数图象上是否存在点N,使得以A、B、M、N为顶点的四边形是平行四边形?若存在,直接写出所有符合条件的点N的坐标,若不存在,请说明理由.24. 如图,在▱ABCD中,对角线AC,BD相交于点O,OA=5cm,E,F为直线BD上的两个动点(点E、F始终在▱ABCD的外面),连接AE、CE、CF、AF. (1)、若DEOD,BFOB,
(1)、若DEOD,BFOB,①求证:四边形AFCE为平行四边形;
②若CA平分∠BCD,∠AEC=60°,求AE的长.
(2)、若DEOD,BFOB,四边形AFCE还是平行四边形吗?请写出结论并说明理由.(3)、若DEOD,BFOB,四边形AFCE还是平行四边形吗?请直接写出结论.