浙教版备考2023年中考数学一轮复习57.多边形

试卷更新日期：2022-12-31 类型：一轮复习

进入出卷网下载

一、单选题（每题3分，共30分）

1. 如图，四边形 $ABCD$ 的内角和等于（）

A、 $180 °$ B、 $270 °$ C、 $360 °$ D、 $540 °$

查看试题解析
2. 如图，PA，PB是 $⊙ O$ 的切线，A、B为切点，若 $∠ A O B = 128 °$ ，则 $∠ P$ 的度数为（）

A、 $32 °$ B、 $52 °$ C、 $64 °$ D、 $72 °$

查看试题解析
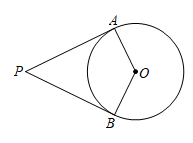3. 如图，将三角形纸片剪掉一角得四边形，设△ABC与四边形BCDE的外角和的度数分别为 $α$ ， $β$ ，则正确的是（）

A、 $α - β = 0$ B、 $α - β < 0$ C、 $α - β > 0$ D、无法比较 $α$ 与 $β$ 的大小

查看试题解析
4. 一个多边形的内角和为900°，则这个多边形是（）

A、七边形 B、八边形 C、九边形 D、十边形

查看试题解析
5. 若从 $n$ 边形的一个顶点出发，可以画出 $4$ 条对角线，则 $n$ 的值是（）

A、 $4$ B、 $5$ C、 $6$ D、 $7$

查看试题解析
6. 如图是不倒翁的主视图，不倒翁的圆形脸恰好与帽子边沿PA，PB分别相切于点A，B，不倒翁的鼻尖正好是圆心O，若∠OAB=28°，则∠APB的度数为（）

A、 $28 °$ B、 $50 °$ C、 $56 °$ D、 $62 °$

查看试题解析
7. 一个多边形从一个顶点可引对角线3条，这个多边形内角和等于（）

A、360° B、540° C、720° D、900°

查看试题解析
8. 用边长相等的两种正多边形进行密铺，其中一种是正八边形，则另一种正多边形可以是（）

A、正三角形 B、正方形 C、正五边形 D、正六边形

查看试题解析
9. 用边长相等的正三角形地砖和正方形地砖铺地面，围绕在一个顶点处正三角形地砖和正方形地砖的块数是（）

A、2块正三角形地砖和2块正方形地砖 B、2块正三角形地砖和3块正方形地砖 C、3块正三角形地砖和2块正方形地砖 D、3块正三角形地砖和3块正方形地砖

查看试题解析
10. 将一长方形纸片沿一条直线剪成两个多边形，那么这两个多边形的内角和之和不可能是（）

A、360° B、540° C、720° D、730°

查看试题解析

二、填空题（共7题，共28分）

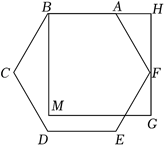
11. 正六边形一个外角的度数为.

查看试题解析
12. 小张同学家要装修，准备购买两种边长相同的正多边形瓷砖用于铺满地面．现已选定正三角形瓷砖，则选的另一种正多边形瓷砖的边数可以是．（填一种即可）

查看试题解析
13. 一个正n边形的一个外角等于36°，则n＝．

查看试题解析
14. 如果正n边形的一个内角与一个外角的比是3：2，则 $n =$ ．

查看试题解析
15. 一个多边形外角和是内角和的 $\frac{2}{9}$ ，则这个多边形的边数为.

查看试题解析
16. 剪纸片：有一张长方形的纸片，用剪刀沿一条不过任何顶点的直线将其剪成了2张纸片；从这2张中任选一张，再用剪刀沿一条不过任何顶点的直线将其剪成了2张纸片，这样共有3张纸片：从这3张中任选一张，再用剪刀沿一条不过任何顶点的直线将其剪成了2张纸片，这样共有4张纸片；……；如此下去，若最后得到10张纸片，其中有1张五边形纸片，3张三角形纸片，5 张四边形纸片，则还有一张多边形纸片的边数为.

查看试题解析
17. 如图，正六边形ABCDEF的顶点A、F分别在正方形BMGH的边BH、GH上.若正方形BMGH的边长为6，则正六边形ABCDEF的边长为 .

查看试题解析

三、解答题（共7题，共62分）

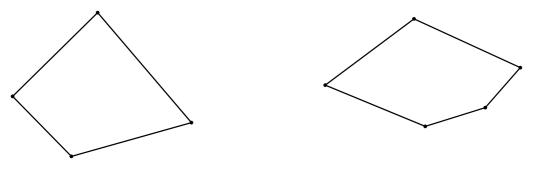
18. 画出图中多边形的所有对角线．

查看试题解析
19. 已知从m边形的一个顶点出发可以画4条对角线；从n边形的一个顶点出发的所有对角线把n边形分成6个三角形．求 $(n - m) (n + m)$ 的值．

查看试题解析
20. 同学们在探索“多边形的内角和”时，利用了“三角形的内角和”.请你在不直接运用结论“n边形的内角和为 $(n - 2) \cdot 180 °$ ”计算的条件下，利用“一个三角形的内角和等于180°”，结合图形说明：五边形 $A B C D E$ 的内角和为540°.

查看试题解析
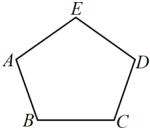21. 夏夏和数学小组的同学们研究多边形对角线的相关问题，邀请你也加入其中，请仔细观察下面的图形和表格，并回答下列问题：
多边形的顶点数
4
5
6
7
8
……
$n$
从一个顶点出发的对角线的条数
1
2
3
4
5
……
①____
多边形对角线的总条数
2
5
9
14
20
……
② ____

(1)、观察探究：请自己观察上面的图形和表格，并用含n的代数式将上面的表格填写完整，其中①；②.

(2)、拓展应用：
有一个76人的代表团，由于任务需要每两人之间通1次电话（且只通1次电话），他们一共通了多少次电话?

查看试题解析
22. 在日常生活中，观察各种建筑物的地板，就能发现地板常用各种正多边形地砖铺砌成美丽的图案．也就是说，使用给定的某些正多边形，能够拼成一个平面图形，既不留下一丝空白，又不互相重叠（在几何里叫做平面镶嵌）．这显然与正多边形的内角大小有关．当围绕一点拼在一起的几个多边形的内角加在一起恰好组成一个周角（360°）时，就拼成了一个平面图形．

(1)、请根据下列图形，填写表中空格：

正多边形边数

3

4

5

6

…

正多边形每个内角的度数

…

(2)、如图，如果限于用一种正多边形镶嵌，哪几种正多边形能镶嵌成一个平面图形；

(3)、正三角形，正四边形，正六边形中选一种，再在其他正多边形中选一种，请画出用这两种不同的正多边形镶嵌成的一个平面图形（草图）；并探索这两种正多边形共能镶嵌成几种不同的平面图形？说明你的理由．

查看试题解析
23. 在2020年新冠肺炎疫情期间，某中学响应政府有“停课不停学”的号召，充分利用网络资源进行网上学习，九年级1班的全体同学在自主完成学习任务的同时，彼此关怀，全班每两个同学都通过一次电话，互相勉励，共同提高，如果该班共有48名同学，若每两名同学之间仅通过一次电话，那么全班同学共通过多少次电话呢？我们可以用下面的方式来解决问题．
用点A₁、A₂、A₃…A₄₈分表示第1名同学、第2名同学、第3名同学…第48名同学，把该班级人数x与通电话次数y之间的关系用如图模型表示：

(1)、填写上图中第四个图中y的值为，第五个图中y的值为．

(2)、通过探索发现，通电话次数y与该班级人数x之间的关系式为，当x＝48时，对应的y＝．

(3)、若九年级1班全体女生相互之间共通话190次，问：该班共有多少名女生？

查看试题解析
24. 已知：如图， $n$ 边形 $A_{1} A_{2} A_{3} A_{4} A_{5} … A_{n}$ .

(1)、求证： $n$ 边形 $A_{1} A_{2} A_{3} A_{4} A_{5} … A_{n}$ 的内角和等于 $(n - 2) \cdot 180 °$ ；

(2)、在一个各内角都相等的多边形中，每一个内角都比相邻的外角的3倍还大20°，求这个多边形的内角和；

(3)、粗心的小明在计算一个多边形的内角和时，误把一个外角也加进去了，得其和为1180°，这个多加的外角度数为，多边形的边数为 .

查看试题解析

多边形的顶点数	4	5	6	7	8	……	$n$
从一个顶点出发的对角线的条数	1	2	3	4	5	……	①____
多边形对角线的总条数	2	5	9	14	20	……	② ____

正多边形边数	3	4	5	6	…
正多边形每个内角的度数					…