浙教版备考2023年中考数学一轮复习56.三角形的综合
试卷更新日期:2022-12-31 类型:一轮复习
一、单选题(每题2分,共20分)
-
1. 中,厘米,厘米,点D为AB的中点.如果点P在线段BC上以v厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.若点Q的运动速度为3厘米/秒,则当与全等时,v的值为( )
 A、2.5 B、3 C、2.25或3 D、1或52. 已知点O是边长为6的等边△ABC的中心,点P在△ABC外,△ABC,△PAB,△PBC,△PCA的面积分别记为 , , , . 若 , 则线段OP长的最小值是( )A、 B、 C、 D、3. 如图,M,A,N是直线l上的三点,AM=3 , AN=5, P是直线l外一点,且∠PAN=60°, AP=1, 若动点Q从点M出发,向点N移动,移动到点N停止,在△APQ形状的变化过程中,依次出现的特殊三角形是( )
A、2.5 B、3 C、2.25或3 D、1或52. 已知点O是边长为6的等边△ABC的中心,点P在△ABC外,△ABC,△PAB,△PBC,△PCA的面积分别记为 , , , . 若 , 则线段OP长的最小值是( )A、 B、 C、 D、3. 如图,M,A,N是直线l上的三点,AM=3 , AN=5, P是直线l外一点,且∠PAN=60°, AP=1, 若动点Q从点M出发,向点N移动,移动到点N停止,在△APQ形状的变化过程中,依次出现的特殊三角形是( ) A、直角三角形—等边三角形—直角三角形—等腰三角形 B、直角三角形—等腰三角形—直角三角形—等边三角形 C、等腰三角形—直角三角形—等腰三角形—直角三角形 D、等腰三角形—直角三角形—等边三角形—直角三角形4. 如图,和都是边长为2的等边三角形,它们的边BC,EF在同一条直线l上,点C,E重合.现将在直线l向右移动,直至点B与F重合时停止移动.在此过程中,设点C移动的距离为x,两个三角形重叠部分的面积为y,则y随x变化的函数图象大致为( )
A、直角三角形—等边三角形—直角三角形—等腰三角形 B、直角三角形—等腰三角形—直角三角形—等边三角形 C、等腰三角形—直角三角形—等腰三角形—直角三角形 D、等腰三角形—直角三角形—等边三角形—直角三角形4. 如图,和都是边长为2的等边三角形,它们的边BC,EF在同一条直线l上,点C,E重合.现将在直线l向右移动,直至点B与F重合时停止移动.在此过程中,设点C移动的距离为x,两个三角形重叠部分的面积为y,则y随x变化的函数图象大致为( ) A、
A、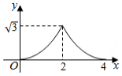 B、
B、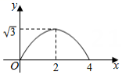 C、
C、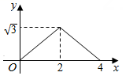 D、
D、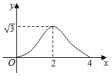 5. 如图, 是等边三角形, ,点M从点C出发沿CB方向以 的速度匀速运动到点B , 同时点N从点C出发沿射线CA方向以 的速度匀速运动,当点M停止运动时,点N也随之停止.过点M作 交AB于点P , 连接MN , NP , 作 关于直线MP对称的 ,设运动时间为ts , 与 重叠部分的面积为 ,则能表示S与t之间函数关系的大致图象为( )
5. 如图, 是等边三角形, ,点M从点C出发沿CB方向以 的速度匀速运动到点B , 同时点N从点C出发沿射线CA方向以 的速度匀速运动,当点M停止运动时,点N也随之停止.过点M作 交AB于点P , 连接MN , NP , 作 关于直线MP对称的 ,设运动时间为ts , 与 重叠部分的面积为 ,则能表示S与t之间函数关系的大致图象为( ) A、
A、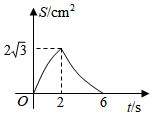 B、
B、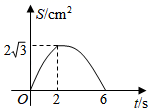 C、
C、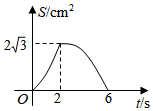 D、
D、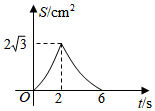 6. 如图,O是正△ABC内一点,OA=3,OB=4,OC=5,将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′,下列结论:①△BO′A可以由△BOC绕点B逆时针旋转60°得到;②点O与O′的距离为4;③∠AOB=150°;④S四边形AOBO;⑤S△AOC+S△AOB= . 其中正确的结论是( )
6. 如图,O是正△ABC内一点,OA=3,OB=4,OC=5,将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′,下列结论:①△BO′A可以由△BOC绕点B逆时针旋转60°得到;②点O与O′的距离为4;③∠AOB=150°;④S四边形AOBO;⑤S△AOC+S△AOB= . 其中正确的结论是( )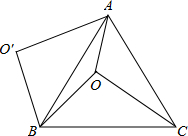 A、①②③⑤ B、①②③④ C、①②③④⑤ D、①②③7. 如图,在中,是的平分线,是外角的平分线,于点E,于点D,连接 . 若 , , , 则的长是( )
A、①②③⑤ B、①②③④ C、①②③④⑤ D、①②③7. 如图,在中,是的平分线,是外角的平分线,于点E,于点D,连接 . 若 , , , 则的长是( )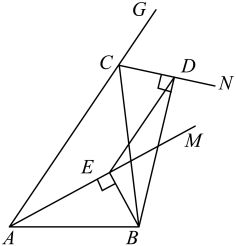 A、 B、 C、 D、8. 如图,在中, , 点为线段上一动点不与点 , 重合 , 连接 , 作 , 交线段于点下列结论:
A、 B、 C、 D、8. 如图,在中, , 点为线段上一动点不与点 , 重合 , 连接 , 作 , 交线段于点下列结论:;
若 , 则;
当时,则为中点;
当为等腰三角形时, .
其中正确的有个.( )
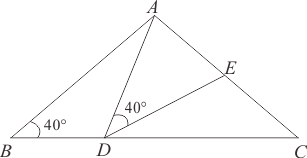 A、1个 B、2个 C、3个 D、4个9. 如图,ABC的三条边相等,三个内角也相等,且 , 连接DE,DF,EF,CD与BE交于H点,以下结论:①;②BDE与CFD的面积相等;③;④ . 其中正确的是( )
A、1个 B、2个 C、3个 D、4个9. 如图,ABC的三条边相等,三个内角也相等,且 , 连接DE,DF,EF,CD与BE交于H点,以下结论:①;②BDE与CFD的面积相等;③;④ . 其中正确的是( )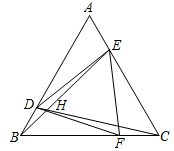 A、①②③④ B、①② C、②③④ D、③④10. 在锐角 中,分别以AB和AC为斜边向 的外侧作等腰 和等腰 ,点D、E、F分别为边AB、AC、BC的中点,连接MD、MF、FE、FN . 根据题意小明同学画出草图(如图所示),并得出下列结论:① ,② ,③ ,④ ,其中结论正确的个数为( )
A、①②③④ B、①② C、②③④ D、③④10. 在锐角 中,分别以AB和AC为斜边向 的外侧作等腰 和等腰 ,点D、E、F分别为边AB、AC、BC的中点,连接MD、MF、FE、FN . 根据题意小明同学画出草图(如图所示),并得出下列结论:① ,② ,③ ,④ ,其中结论正确的个数为( )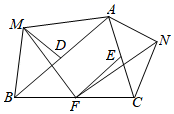 A、4 B、3 C、2 D、1
A、4 B、3 C、2 D、1二、填空题(每题2分,共12分)
-
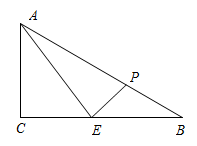
11. 如图,在中, , BC=8cm,AC=6cm,点E是BC的中点,动点P从A点出发,以每秒1cm的速度沿运动.若设点P运动的时间是t秒,那么当 , 的面积等于6.
 12. 如图,在△ABC中,AB=AC=4,∠CAB=30°,AD⊥BC,垂足为D,P为线段AD上的一动点,连接PB、PC.则PA+2PB的最小值为 .
12. 如图,在△ABC中,AB=AC=4,∠CAB=30°,AD⊥BC,垂足为D,P为线段AD上的一动点,连接PB、PC.则PA+2PB的最小值为 .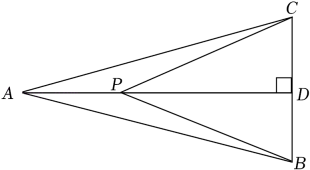 13. 如图,在 中, , , .若点P是 内一点,则 的最小值为 .
13. 如图,在 中, , , .若点P是 内一点,则 的最小值为 . 14. 如图,是等边三角形, , D是的中点,F是直线上一动点,线段绕点D逆时针旋转 , 得到线段 , 当点F运动时,的最小值是 .
14. 如图,是等边三角形, , D是的中点,F是直线上一动点,线段绕点D逆时针旋转 , 得到线段 , 当点F运动时,的最小值是 .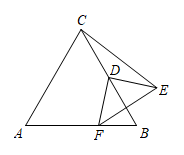 15. 如图,在中, , , , 点P在的内部(不包括边上),且的面积等于的面积的一半,设点D为的重心,点P、D两点之间的距离为d,那么d的最小值为 .
15. 如图,在中, , , , 点P在的内部(不包括边上),且的面积等于的面积的一半,设点D为的重心,点P、D两点之间的距离为d,那么d的最小值为 . 16. 如图,在Rt中, , 动点D从点A出发,沿线段以每秒2个单位的速度向B运动,过点D作交所在的直线于点F,连结 , 设点D运动时间为t秒,当是等腰三角形时,则t=秒.
16. 如图,在Rt中, , 动点D从点A出发,沿线段以每秒2个单位的速度向B运动,过点D作交所在的直线于点F,连结 , 设点D运动时间为t秒,当是等腰三角形时,则t=秒.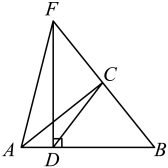
三、综合题(共10题,共88分)
-
17. 已知△ABC中,∠ACB=90°,AC=BC=4cm,点P从点A出发,沿AB方向以每秒cm的速度向终点B运动,同时动点Q从点B出发沿BC方向以每秒1cm的速度向终点C运动,设运动的时间为t秒.
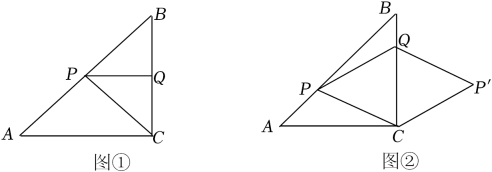 (1)、如图①,若PQ⊥BC,求t的值;(2)、如图②,将△PQC沿BC翻折至△P′QC,当t为何值时,四边形QPCP′为菱形?18. 如图1,在中,于点D,在DA上取点E,使 , 连接BE、CE.
(1)、如图①,若PQ⊥BC,求t的值;(2)、如图②,将△PQC沿BC翻折至△P′QC,当t为何值时,四边形QPCP′为菱形?18. 如图1,在中,于点D,在DA上取点E,使 , 连接BE、CE.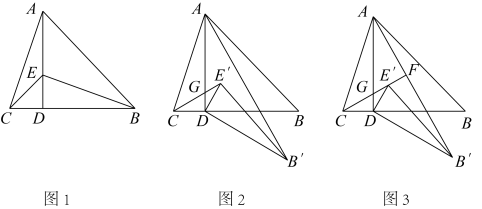 (1)、直接写出CE与AB的位置关系;(2)、如图2,将绕点D旋转,得到(点 , 分别与点B,E对应),连接 , 在旋转的过程中与的位置关系与(1)中的CE与AB的位置关系是否一致?请说明理由;(3)、如图3,当绕点D顺时针旋转30°时,射线与AD、分别交于点G、F,若 , 求的长.19. 在△ABC中,AB=AC,∠BAC=90°,AD是△ABC的角平分线.
(1)、直接写出CE与AB的位置关系;(2)、如图2,将绕点D旋转,得到(点 , 分别与点B,E对应),连接 , 在旋转的过程中与的位置关系与(1)中的CE与AB的位置关系是否一致?请说明理由;(3)、如图3,当绕点D顺时针旋转30°时,射线与AD、分别交于点G、F,若 , 求的长.19. 在△ABC中,AB=AC,∠BAC=90°,AD是△ABC的角平分线.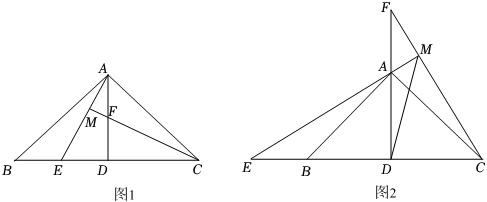 (1)、如图1,点E、F分别是线段BD、AD上的点,且DE=DF,AE与CF的延长线交于点M,则AE与CF的数量关系是 , 位置关系是;(2)、如图2,点E、F分别在DB和DA的延长线上,且DE=DF,EA的延长线交CF于点M.
(1)、如图1,点E、F分别是线段BD、AD上的点,且DE=DF,AE与CF的延长线交于点M,则AE与CF的数量关系是 , 位置关系是;(2)、如图2,点E、F分别在DB和DA的延长线上,且DE=DF,EA的延长线交CF于点M.①(1)中的结论还成立吗?如果成立,请给出证明;如果不成立,请说明理由;
②连接DM,求∠EMD的度数;
③若DM=6 , ED=12,求EM的长.
20. 如图,△AOB是等边三角形,过点A作y轴的垂线,垂足为C,点C的坐标为(0,).P是直线AB上在第一象限内的一动点,过点P作y轴的垂线,垂足为D,交AO于点E,连接AD,作DM⊥AD交x轴于点M,交AO于点F,连接BE,BF. (1)、填空:若△AOD是等腰三角形,则点D的坐标为;(2)、当点P在线段AB上运动时(点P不与点A,B重合),设点M的横坐标为m.
(1)、填空:若△AOD是等腰三角形,则点D的坐标为;(2)、当点P在线段AB上运动时(点P不与点A,B重合),设点M的横坐标为m.①求m值最大时点D的坐标;
②是否存在这样的m值,使BE=BF?若存在,求出此时的m值;若不存在,请说明理由.
21. 【思维探究】如图1,在四边形ABCD中,∠BAD=60°,∠BCD=120°,AB=AD,连接AC.求证:BC+CD=AC.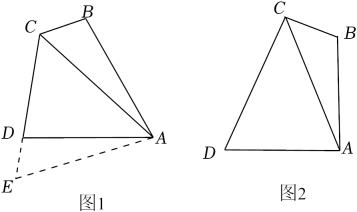 (1)、小明的思路是:延长CD到点E,使DE=BC,连接AE.根据∠BAD+∠BCD=180°,推得∠B+∠ADC=180°,从而得到∠B=∠ADE,然后证明ADE≌ABC,从而可证BC+CD=AC,请你帮助小明写出完整的证明过程.(2)、【思维延伸】如图2,四边形ABCD中,∠BAD=∠BCD=90°,AB=AD,连接AC,猜想BC,CD,AC之间的数量关系,并说明理由.(3)、【思维拓展】在四边形ABCD中,∠BAD=∠BCD=90°,AB=AD= , AC与BD相交于点O.若四边形ABCD中有一个内角是75°,请直接写出线段OD的长.22. 如图
(1)、小明的思路是:延长CD到点E,使DE=BC,连接AE.根据∠BAD+∠BCD=180°,推得∠B+∠ADC=180°,从而得到∠B=∠ADE,然后证明ADE≌ABC,从而可证BC+CD=AC,请你帮助小明写出完整的证明过程.(2)、【思维延伸】如图2,四边形ABCD中,∠BAD=∠BCD=90°,AB=AD,连接AC,猜想BC,CD,AC之间的数量关系,并说明理由.(3)、【思维拓展】在四边形ABCD中,∠BAD=∠BCD=90°,AB=AD= , AC与BD相交于点O.若四边形ABCD中有一个内角是75°,请直接写出线段OD的长.22. 如图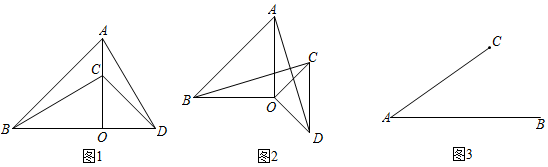 (1)、如图1,和是等腰直角三角形, , 点C在OA上,点D在线段BO延长线上,连接AD,BC.线段AD与BC的数量关系为;(2)、如图2,将图1中的绕点O顺时针旋转()第一问的结论是否仍然成立;如果成立,证明你的结论,若不成立,说明理由.(3)、如图,若 , 点C是线段AB外一动点, , 连接BC,
(1)、如图1,和是等腰直角三角形, , 点C在OA上,点D在线段BO延长线上,连接AD,BC.线段AD与BC的数量关系为;(2)、如图2,将图1中的绕点O顺时针旋转()第一问的结论是否仍然成立;如果成立,证明你的结论,若不成立,说明理由.(3)、如图,若 , 点C是线段AB外一动点, , 连接BC,①若将CB绕点C逆时针旋转90°得到CD,连接AD,则AD的最大值 ▲ ;
②若以BC为斜边作 , (B、C、D三点按顺时针排列), , 连接AD,当时,直接写出AD的值.
23. 综合与实践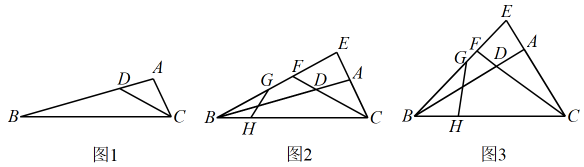 (1)、问题情境:
(1)、问题情境:数学活动课上,王老师出示了一个问题:如图1,在中,D是上一点, . 求证 .
独立思考:
请解答王老师提出的问题.
(2)、实践探究:在原有问题条件不变的情况下,王老师增加下面的条件,并提出新问题,请你解答.“如图2,延长至点E,使 , 与的延长线相交于点F,点G,H分别在上, , . 在图中找出与相等的线段,并证明.”
(3)、问题解决:数学活动小组河学时上述问题进行特殊化研究之后发现,当时,若给出中任意两边长,则图3中所有已经用字母标记的线段长均可求,该小组提出下面的问题,请你解答.“如图3,在(2)的条件下,若 , , , 求的长.”
24.(1)、【问题呈现】如图1,△ABC和△ADE都是等边三角形,连接BD,CE.求证:BD=CE.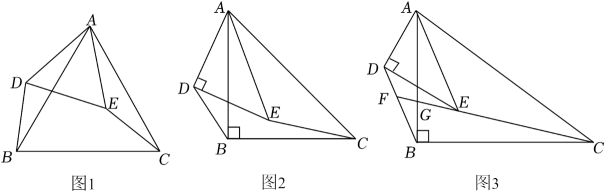 (2)、【类比探究】如图2,△ABC和△ADE都是等腰直角三角形,∠ABC=∠ADE=90°.连接BD,CE.请直接写出的值.(3)、【拓展提升】如图3,△ABC和△ADE都是直角三角形,∠ABC=∠ADE=90°,且== . 连接BD,CE.
(2)、【类比探究】如图2,△ABC和△ADE都是等腰直角三角形,∠ABC=∠ADE=90°.连接BD,CE.请直接写出的值.(3)、【拓展提升】如图3,△ABC和△ADE都是直角三角形,∠ABC=∠ADE=90°,且== . 连接BD,CE.①求的值;
②延长CE交BD于点F,交AB于点G.求sin∠BFC的值.
25.(1)、【情境再现】甲、乙两个含角的直角三角尺如图①放置,甲的直角顶点放在乙斜边上的高的垂足O处,将甲绕点O顺时针旋转一个锐角到图②位置.小莹用作图软件Geogebra按图②作出示意图,并连接 , 如图③所示,交于E,交于F,通过证明 , 可得 .
请你证明: .
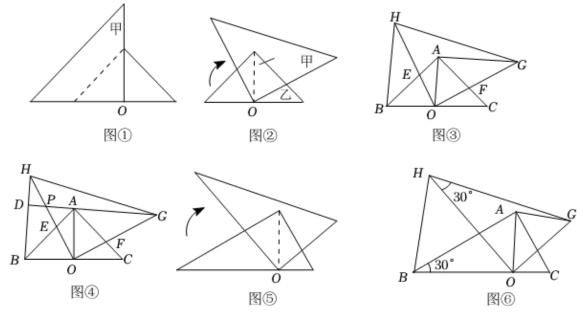 (2)、【迁移应用】
(2)、【迁移应用】延长分别交所在直线于点P,D,如图④,猜想并证明与的位置关系.
(3)、【拓展延伸】小亮将图②中的甲、乙换成含角的直角三角尺如图⑤,按图⑤作出示意图,并连接 , 如图⑥所示,其他条件不变,请你猜想并证明与的数量关系.
26. 已知 ,点A,B分别在射线 上运动, .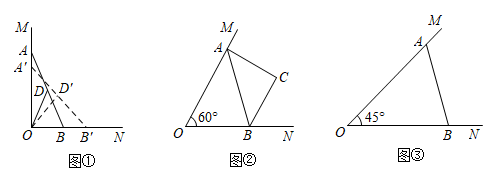 (1)、如图①,若 ,取AB中点D,点A,B运动时,点D也随之运动,点A,B,D的对应点分别为 ,连接 .判断OD与 有什么数量关系?证明你的结论:(2)、如图②,若 ,以AB为斜边在其右侧作等腰直角三角形ABC,求点O与点C的最大距离:(3)、如图③,若 ,当点A,B运动到什么位置时, 的面积最大?请说明理由,并求出 面积的最大值.
(1)、如图①,若 ,取AB中点D,点A,B运动时,点D也随之运动,点A,B,D的对应点分别为 ,连接 .判断OD与 有什么数量关系?证明你的结论:(2)、如图②,若 ,以AB为斜边在其右侧作等腰直角三角形ABC,求点O与点C的最大距离:(3)、如图③,若 ,当点A,B运动到什么位置时, 的面积最大?请说明理由,并求出 面积的最大值.