浙教版备考2023年中考数学一轮复习55.勾股定理及其应用
试卷更新日期:2022-12-31 类型:一轮复习
一、单选题(每题3分,共30分)
-
1. 如图,在中, , D是AB的中点,延长CB至点E,使 , 连接DE,F为DE中点,连接BF.若 , , 则BF的长为( )
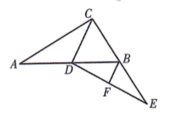 A、5 B、4 C、6 D、82. 如图,三角形纸片ABC中,∠BAC=90°,AB=2,AC=3.沿过点A的直线将纸片折叠,使点B落在边BC上的点D处;再折叠纸片,使点C与点D重合,若折痕与AC的交点为E,则AE的长是( )
A、5 B、4 C、6 D、82. 如图,三角形纸片ABC中,∠BAC=90°,AB=2,AC=3.沿过点A的直线将纸片折叠,使点B落在边BC上的点D处;再折叠纸片,使点C与点D重合,若折痕与AC的交点为E,则AE的长是( ) A、 B、 C、 D、3. 如图,在Rt△ABC中, , , , 将绕点B顺时针旋转90°得到.在此旋转过程中所扫过的面积为( )
A、 B、 C、 D、3. 如图,在Rt△ABC中, , , , 将绕点B顺时针旋转90°得到.在此旋转过程中所扫过的面积为( ) A、25π+24 B、5π+24 C、25π D、5π4. 如图,在正方形方格纸中,每个小正方形的边长都相等,A,B,C,D都在格点处,AB与CD相交于点P,则cos∠APC的值为( )
A、25π+24 B、5π+24 C、25π D、5π4. 如图,在正方形方格纸中,每个小正方形的边长都相等,A,B,C,D都在格点处,AB与CD相交于点P,则cos∠APC的值为( ) A、 B、 C、 D、5. 如图,正方形的对角线交于点O,点E是直线上一动点.若 , 则的最小值是( )
A、 B、 C、 D、5. 如图,正方形的对角线交于点O,点E是直线上一动点.若 , 则的最小值是( ) A、 B、 C、 D、6. 如图是两个全等的直角三角形拼成的图形,且点 , , 在同一直线上,连结设 , , 则的面积可以表示为( )
A、 B、 C、 D、6. 如图是两个全等的直角三角形拼成的图形,且点 , , 在同一直线上,连结设 , , 则的面积可以表示为( ) A、 B、 C、 D、7. 如图,正方形ABCD边长为1,以AC为边作第2个正方形ACEF,再以CF为边作第3个正方形FCGH,…,按照这样的规律作下去,第6个正方形的边长为( )
A、 B、 C、 D、7. 如图,正方形ABCD边长为1,以AC为边作第2个正方形ACEF,再以CF为边作第3个正方形FCGH,…,按照这样的规律作下去,第6个正方形的边长为( ) A、(2)5 B、(2)6 C、()5 D、()68. 有一直角三角形纸片,∠C=90°BC=6,AC=8,现将△ABC按如图那样折叠,使点A与点B重合,折痕为DE,则CE的长为( )
A、(2)5 B、(2)6 C、()5 D、()68. 有一直角三角形纸片,∠C=90°BC=6,AC=8,现将△ABC按如图那样折叠,使点A与点B重合,折痕为DE,则CE的长为( )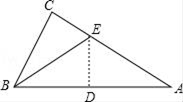 A、 B、 C、 D、49. 我国古代数学著作《九章算术》中记载了一个问题:“今有池方一丈,葭(jiǎ)生其中,出水一尺,引葭赴岸,适与岸齐.间水深几何.”(丈、尺是长度单位,1丈 尺,)其大意为:有一个水池,水面是一个边长为10尺的正方形,在水池正中央有一根芦苇,它高出水面1尺.如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面,水的深度是多少?则水深为( )
A、 B、 C、 D、49. 我国古代数学著作《九章算术》中记载了一个问题:“今有池方一丈,葭(jiǎ)生其中,出水一尺,引葭赴岸,适与岸齐.间水深几何.”(丈、尺是长度单位,1丈 尺,)其大意为:有一个水池,水面是一个边长为10尺的正方形,在水池正中央有一根芦苇,它高出水面1尺.如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面,水的深度是多少?则水深为( ) A、10尺 B、11尺 C、12尺 D、13尺10. 数形结合是数学的重要思想和解题方法,如:“当0<x<12时,求代数式 的最小值”,其中 可看作两直角边分别为x和2的Rt△ACP的斜边长, 可看作两直角边分别是12-x和3的Rt△BDP的斜边长.于是将问题转化为求AP+BP的最小值,如图所示,当AP与BP共线时,AP+BP为最小.请你解决问题:当0<x<4时,则代数式 的最小值是( )
A、10尺 B、11尺 C、12尺 D、13尺10. 数形结合是数学的重要思想和解题方法,如:“当0<x<12时,求代数式 的最小值”,其中 可看作两直角边分别为x和2的Rt△ACP的斜边长, 可看作两直角边分别是12-x和3的Rt△BDP的斜边长.于是将问题转化为求AP+BP的最小值,如图所示,当AP与BP共线时,AP+BP为最小.请你解决问题:当0<x<4时,则代数式 的最小值是( ) A、4 B、5 C、6 D、7
A、4 B、5 C、6 D、7二、填空题(每题3分,共18分)
-
11. 如图,将矩形纸片ABCD沿CE折叠,使点B落在边AD上的点F处.若点E在边AB上,AB=3,BC=5,则AE= .
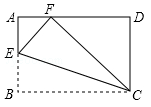 12. 如图,在 中, , 是 边上除 , 点外的任意一点,则 .
12. 如图,在 中, , 是 边上除 , 点外的任意一点,则 . 13. 沐沐用七巧板拼了一个对角线长为2的正方形,再用这副七巧板拼成一个长方形(如图所示),则长方形的对角线长为 .
13. 沐沐用七巧板拼了一个对角线长为2的正方形,再用这副七巧板拼成一个长方形(如图所示),则长方形的对角线长为 . 14. 如图所示的象棋盘中,各个小正方形的边长均为1.“马”从图中的位置出发,不走重复路线,按照“马走日”的规则,走两步后的落点与出发点间的最短距离为.
14. 如图所示的象棋盘中,各个小正方形的边长均为1.“马”从图中的位置出发,不走重复路线,按照“马走日”的规则,走两步后的落点与出发点间的最短距离为.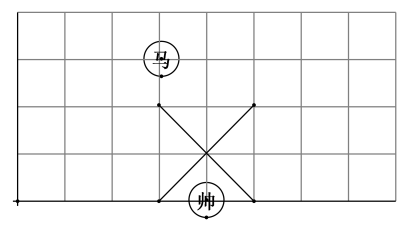 15. 我国古代数学家赵爽创制了一幅“赵爽弦图”,极富创新意识地给出了勾股定理的证明.如图所示,“赵爽弦图”是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形,若大正方形的面积是25,小正方形的面积是1,则.
15. 我国古代数学家赵爽创制了一幅“赵爽弦图”,极富创新意识地给出了勾股定理的证明.如图所示,“赵爽弦图”是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形,若大正方形的面积是25,小正方形的面积是1,则.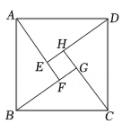 16. 勾股定理最早出现在商高的《周髀算经》:“勾广三,股修四,经隅五”.观察下列勾股数:3,4,5;5,12,13;7,24,25;…,这类勾股数的特点是:勾为奇数,弦与股相差为1,柏拉图研究了勾为偶数,弦与股相差为2的一类勾股数,如:6,8,10;8,15,17;…,若此类勾股数的勾为2m(m≥3,m为正整数),则其弦是(结果用含m的式子表示).
16. 勾股定理最早出现在商高的《周髀算经》:“勾广三,股修四,经隅五”.观察下列勾股数:3,4,5;5,12,13;7,24,25;…,这类勾股数的特点是:勾为奇数,弦与股相差为1,柏拉图研究了勾为偶数,弦与股相差为2的一类勾股数,如:6,8,10;8,15,17;…,若此类勾股数的勾为2m(m≥3,m为正整数),则其弦是(结果用含m的式子表示).三、解答题(共8题,共72分)
-
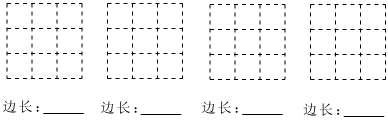
17. 在的网格中,设每一个小方格的边长为1个单位,画出4个不同的正方形用阴影部分表示 , 所画正方形的顶点都在方格的顶点上,且面积均小于9,并写出相应正方形的边长.
 18. 如图,在离水面高度为5米的岸上,有人用绳子拉船靠岸,开始时绳子BC的长为13米,此人以0.5米/秒的速度收绳,10秒后船移动到点D的位置,问船向岸边移动了多少米?(假设绳子是直的,结果保留根号)
18. 如图,在离水面高度为5米的岸上,有人用绳子拉船靠岸,开始时绳子BC的长为13米,此人以0.5米/秒的速度收绳,10秒后船移动到点D的位置,问船向岸边移动了多少米?(假设绳子是直的,结果保留根号) 19. 已知的三条边长分别为 , , , 其中 , , , 且是直角三角形吗?请证明你的判断.20. 阅读与应用:
19. 已知的三条边长分别为 , , , 其中 , , , 且是直角三角形吗?请证明你的判断.20. 阅读与应用:下面是小敏学习实数之后,写的数学日记的一部分,请你认真阅读,并完成相应的任务.
2022年9月22日 天气:晴
无理数与线段长.今天我们借助勾股定理,在数轴上找到了一些特殊的无理数对应的点,认识了“数轴上的点与实数一一对应”这一事实.
回顾梳理:要在数轴上找到表示的点,关键是在数轴上构造线段 . 如图1,正方形的边长为1个单位长度,以原点O为圆心,对角线长为半径画弧与数轴分别交于点A, , 则点A对应的数为 , 点对应的数为 . 类似地,我们可以在数轴上找到表示 , , …的点.
拓展思考:如图2,改变图1中正方形的位置,用类似的方法作图,可在数轴上构造出线段与 , 其中O仍为原点,点B,分别在原点的右侧、左侧,可由线段与的长得到点B,所表示的无理数!
按照这样的思路,只要构造出特定长度的线段,就能在数轴上找到无理数对应的点!

任务:
(1)、“拓展思考”中,线段的长为 , 的长为;点B表示的数为 , 点表示的数为 .(2)、请从A,B两题中任选一题作答.我选择题.A.请在图3所示的数轴上,画图确定表示的点M,N;
B.请在图3所示的数轴上,画图确定表示的点M.
 21. 综合与实践
21. 综合与实践 (1)、知识再现
(1)、知识再现
如图 , 中, , 分别以、、为边向外作的正方形的面积为、、 . 当 , 时, .(2)、问题探究如图,中, .
如图 , 分别以、、为边向外作的等腰直角三角形的面积为、、 , 则、、之间的数量关系是 .(3)、如图 , 分别以、、为边向外作的等边三角形的面积为、、 , 试猜想、、之间的数量关系,并说明理由.(4)、实践应用
如图4,将图中的绕点逆时针旋转一定角度至 , 绕点顺时针旋转一定角度至 , 、相交于点 . 求证:;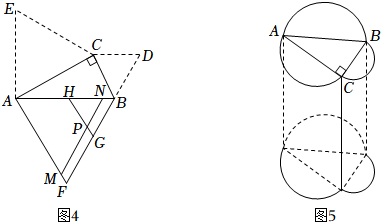 (5)、如图5,分别以图中的边、、为直径向外作半圆,再以所得图形为底面作柱体,、、为直径的半圆柱的体积分别为、、 . 若 , 柱体的高 , 直接写出的值.22. 【经典回顾】
(5)、如图5,分别以图中的边、、为直径向外作半圆,再以所得图形为底面作柱体,、、为直径的半圆柱的体积分别为、、 . 若 , 柱体的高 , 直接写出的值.22. 【经典回顾】梅文鼎是我国清初著名的数学家,他在《勾股举隅》中给出多种证明勾股定理的方法图1是其中一种方法的示意图及部分辅助线.

在中, , 四边形、和分别是以的三边为一边的正方形.延长和 , 交于点 , 连接并延长交于点 , 交于点 , 延长交于点 .
(1)、证明:;(2)、证明:正方形的面积等于四边形的面积;(3)、请利用(2)中的结论证明勾股定理.(4)、【迁移拓展】如图2,四边形和分别是以的两边为一边的平行四边形,探索在下方是否存在平行四边形 , 使得该平行四边形的面积等于平行四边形、的面积之和.若存在,作出满足条件的平行四边形(保留适当的作图痕迹);若不存在,请说明理由.
23. 综合与实践(1)、问题情境:在Rt△ABC中,∠BAC=90°,AB=6,AC=8.直角三角板EDF中∠EDF=90°,将三角板的直角顶点D放在Rt△ABC斜边BC的中点处,并将三角板绕点D旋转,三角板的两边DE,DF分别与边AB,AC交于点M,N,猜想证明:
如图①,在三角板旋转过程中,当点M为边AB的中点时,试判断四边形AMDN的形状,并说明理由;
(2)、问题解决:如图②,在三角板旋转过程中,当时,求线段CN的长;
(3)、如图③,在三角板旋转过程中,当AM=AN时,直接写出线段AN的长.24. 将矩形纸片放在平面直角坐标系中,点 , 点 , 点 . 现绕点O顺时针旋转矩形纸片 , 得到新的矩形 , 其中A,B,C的对应点分别为 . 当直线与直线有交点时,设交点为D. (1)、在旋转过程中,判断线段和的数量关系,并以图①为例说明理由;(2)、在旋转过程中,当点落在线段上时(如图②),直接写出点的坐标;(3)、在旋转过程中,若线段恰好过线段中点E时(如图③),求线段的长;(4)、在旋转过程中,当线段与线段的交点M恰好是线段中点时(如图④),请直接写出点M和点D的坐标.
(1)、在旋转过程中,判断线段和的数量关系,并以图①为例说明理由;(2)、在旋转过程中,当点落在线段上时(如图②),直接写出点的坐标;(3)、在旋转过程中,若线段恰好过线段中点E时(如图③),求线段的长;(4)、在旋转过程中,当线段与线段的交点M恰好是线段中点时(如图④),请直接写出点M和点D的坐标.