浙教版备考2023年中考数学一轮复习54.直角三角形的性质和判定
试卷更新日期:2022-12-31 类型:一轮复习
一、单选题(每题3分,共30分)
-
1. 如图,在△ABC中,∠ACB=90°,CD是AB边上的高,∠A=30°,则下列结论中正确的是( )
 A、AD=2CD B、CD=2BD C、AC=2BC D、AB=4BD2. 在△ABC中,BC=+1,∠B=45°,∠C=30°,则△ABC的面积为( )
A、AD=2CD B、CD=2BD C、AC=2BC D、AB=4BD2. 在△ABC中,BC=+1,∠B=45°,∠C=30°,则△ABC的面积为( ) A、 B、+1 C、 D、+13. 如图,△ABD和△CBD,∠ADB=90°,∠ABD=∠DBC,AD=DC=1,若AB=4,则BC的长为( )
A、 B、+1 C、 D、+13. 如图,△ABD和△CBD,∠ADB=90°,∠ABD=∠DBC,AD=DC=1,若AB=4,则BC的长为( ) A、 B、2 C、3 D、4. 如图,∠AOE=15°,OE平分∠AOB,DE∥OB交OA于点D,EC⊥OB,垂足为C.若EC=2,则OD的长为( )
A、 B、2 C、3 D、4. 如图,∠AOE=15°,OE平分∠AOB,DE∥OB交OA于点D,EC⊥OB,垂足为C.若EC=2,则OD的长为( ) A、2 B、2 C、4 D、4+25. 如图,已知⊙O的直径为4,∠ACB=45°,则AB的长为( )
A、2 B、2 C、4 D、4+25. 如图,已知⊙O的直径为4,∠ACB=45°,则AB的长为( ) A、4 B、2 C、4 D、26. 由四个全等的直角三角形和一个小正方形组成的大正方形ABCD如图所示.过点D作DF的垂线交小正方形对角线EF的延长线于点G,连结BG,若大正方形的面积是小正方形面积的5倍,则 的值为( )
A、4 B、2 C、4 D、26. 由四个全等的直角三角形和一个小正方形组成的大正方形ABCD如图所示.过点D作DF的垂线交小正方形对角线EF的延长线于点G,连结BG,若大正方形的面积是小正方形面积的5倍,则 的值为( ) A、 B、3 C、 D、47. 活动探究:我们知道,已知两边和其中一边的对角对应相等的两个三角形不一定全等,如已知△ABC中,∠A=30°, AC=3,∠A所对的边为 , 满足已知条件的三角形有两个(我们发现其中如图的△ABC是一个直角三角形),则满足已知条件的三角形的第三边长为( )
A、 B、3 C、 D、47. 活动探究:我们知道,已知两边和其中一边的对角对应相等的两个三角形不一定全等,如已知△ABC中,∠A=30°, AC=3,∠A所对的边为 , 满足已知条件的三角形有两个(我们发现其中如图的△ABC是一个直角三角形),则满足已知条件的三角形的第三边长为( ) A、 B、 C、或 D、或8. 如图,在等腰直角三角形中, , 为的中点,为边上一点不与端点重合 , 过点作于点 , 作于点 , 过点作交的延长线于点若 , 则阴影部分的面积为( )
A、 B、 C、或 D、或8. 如图,在等腰直角三角形中, , 为的中点,为边上一点不与端点重合 , 过点作于点 , 作于点 , 过点作交的延长线于点若 , 则阴影部分的面积为( ) A、12 B、12.5 C、13 D、13.59. 在2022年北京冬奥会开幕式和闭幕式中,一片“雪花”的故事展现了“世界大同、天下一家”的主题,让世界观众感受了中国人的浪漫,如图,将“雪花”图案(边长为4的正六边形ABCDEF)放在平面直角坐标系中,若AB与x轴垂直,顶点A的坐标为(2,-3).则顶点C的坐标为( )
A、12 B、12.5 C、13 D、13.59. 在2022年北京冬奥会开幕式和闭幕式中,一片“雪花”的故事展现了“世界大同、天下一家”的主题,让世界观众感受了中国人的浪漫,如图,将“雪花”图案(边长为4的正六边形ABCDEF)放在平面直角坐标系中,若AB与x轴垂直,顶点A的坐标为(2,-3).则顶点C的坐标为( )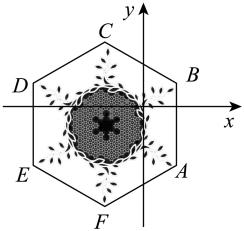 A、 B、 C、 D、10. 如图1是第七届国际数学教育大会()的会徽,在其主体图案中选择两个相邻的直角三角形,恰好能够组合得到如图2所示的四边形.若 , , , 则的值为( )
A、 B、 C、 D、10. 如图1是第七届国际数学教育大会()的会徽,在其主体图案中选择两个相邻的直角三角形,恰好能够组合得到如图2所示的四边形.若 , , , 则的值为( )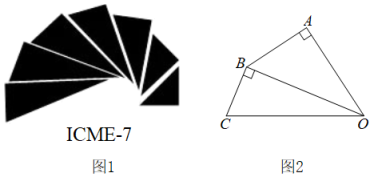 A、 B、 C、 D、1
A、 B、 C、 D、1二、填空题(每题3分,共18分)
-
11. 如图,依下列步骤尺规作图,并保留作图痕迹:
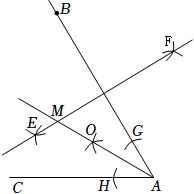
(1)分别以点A,B为圆心,大于AB的长为半径作弧,两弧相交于E,F两点,作直线EF;
(2)以点A为圆心,适当长为半径画弧,分别交AB,AC于点G,H,再分别以点G,H为圆心,大于GH的长为半径画弧,两弧在∠BAC的内部相交于点O,画射线AO,交直线EF于点M.
已知线段AB=6,∠BAC=60°,则点M到射线AC的距离为.12. 已知⊙O的直径AB长为2,弦AC长为 , 那么弦AC所对的圆周角的度数等于 .13. 如图,将绕点旋转得到 , 若 , , , 则 .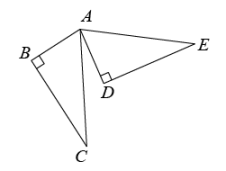 14. 如图,四边形ABCD中,∠ADC=90°,AC⊥BC,∠ABC=45°,AC与BD交于点E,若AB= , CD=2,则△ABE的面积为 .
14. 如图,四边形ABCD中,∠ADC=90°,AC⊥BC,∠ABC=45°,AC与BD交于点E,若AB= , CD=2,则△ABE的面积为 .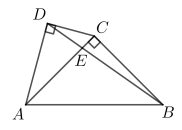 15. 如图,在△ABC中,∠A=30°,∠B=90°,D为AB中点,E在线段AC上, , 则 .
15. 如图,在△ABC中,∠A=30°,∠B=90°,D为AB中点,E在线段AC上, , 则 .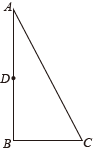 16. 《庄子▪天下篇》记载“一尺之锤,日取其半,万世不竭.”如图,直线与轴交于点 , 过点作轴的平行线交直线于点 , 过点作轴的平行线交直线于点 , 以此类推,令 , , , , 若对任意大于1的整数恒成立,则的最小值为 .
16. 《庄子▪天下篇》记载“一尺之锤,日取其半,万世不竭.”如图,直线与轴交于点 , 过点作轴的平行线交直线于点 , 过点作轴的平行线交直线于点 , 以此类推,令 , , , , 若对任意大于1的整数恒成立,则的最小值为 .
三、解答题(共8题,共66分)
-
17. 方格纸中小正方形的顶点叫格点,点A和点B是格点,位置如图.
 (1)、在图1中确定格点C,使得△ABC是直角三角形,画出一个这样的△ABC,并直接写出线段AB的长.(2)、在图2中确定格点D,使得△ABD是等腰三角形,画出一个这样的△ABD.18. 如图,点 , 在上,且 , , .
(1)、在图1中确定格点C,使得△ABC是直角三角形,画出一个这样的△ABC,并直接写出线段AB的长.(2)、在图2中确定格点D,使得△ABD是等腰三角形,画出一个这样的△ABD.18. 如图,点 , 在上,且 , , . (1)、求证: .(2)、连结 , 若 , , , 求的长度.19. 如图,在矩形ABCD中,AB=BC,点F在BC边的延长线上,点P是线段BC上一点(与点B,C不重合),连接AP并延长,过点C作CG⊥AP,垂足为E.
(1)、求证: .(2)、连结 , 若 , , , 求的长度.19. 如图,在矩形ABCD中,AB=BC,点F在BC边的延长线上,点P是线段BC上一点(与点B,C不重合),连接AP并延长,过点C作CG⊥AP,垂足为E. (1)、若CG为∠DCF的平分线.请判断BP与CP的数量关系,并证明;(2)、若AB=3,△ABP≌△CEP,求BP的长.20. 两个顶角相等的等腰三角形,如果具有公共的顶角的顶点,并把它们的底角顶点连接起来,则形成一组全等的三角形,把具有这个规律的图形称为“手拉手”图形.(1)、问题发现:
(1)、若CG为∠DCF的平分线.请判断BP与CP的数量关系,并证明;(2)、若AB=3,△ABP≌△CEP,求BP的长.20. 两个顶角相等的等腰三角形,如果具有公共的顶角的顶点,并把它们的底角顶点连接起来,则形成一组全等的三角形,把具有这个规律的图形称为“手拉手”图形.(1)、问题发现:如图1,若和是顶角相等的等腰三角形,BC,DE分别是底边.求证:;
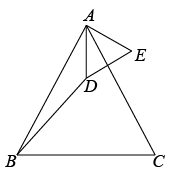
图1
(2)、解决问题:如图2,若和均为等腰直角三角形, , 点A,D,E在同一条直线上,CM为中DE边上的高,连接BE,请判断∠AEB的度数及线段CM,AE,BE之间的数量关系并说明理由.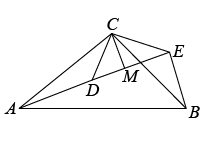
图2
21. 如图,在△ABC中,AC=BC= , ∠ACB=120°,将一块足够大的直角三角尺PEF(∠E=90°,∠EPF=30°)按如图放置,顶点P在线段AB上滑动(不与点A,B重合),三角尺的直角边PE始终经过点C,斜边PF交AC于点D. (1)、当PD∥BC时,判断△BCP的形状,并说明理由;(2)、当△PCD是等腰三角形时,求出所有满足要求的BP的长;(3)、记点C关于PD的对称点为C′,当C′D⊥AC时,AP的长是.22. 如图,在平面直角坐标系中,等腰直角三角形ABO的直角顶点A的坐标为(m,2),点B在x轴上,将△ABO向右平移得到△DEF,使点D恰好在反比例函数y=(x>0)的图象上.
(1)、当PD∥BC时,判断△BCP的形状,并说明理由;(2)、当△PCD是等腰三角形时,求出所有满足要求的BP的长;(3)、记点C关于PD的对称点为C′,当C′D⊥AC时,AP的长是.22. 如图,在平面直角坐标系中,等腰直角三角形ABO的直角顶点A的坐标为(m,2),点B在x轴上,将△ABO向右平移得到△DEF,使点D恰好在反比例函数y=(x>0)的图象上.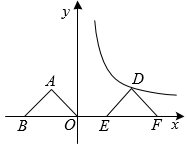 (1)、求m的值和点D的坐标;(2)、求DF所在直线的表达式;(3)、若该反比例函数图象与直线DF的另一交点为点G,求S△EFG.23. 《几何原本》是古希腊数学家欧几里得的一部不朽著作,是数学发展史的一个里程碑.在该书的第2幕“几何与代数”部分,记载了很多利用几何图形来论证的代数结论,利用几何给人以强烈印象将抽象的逻辑规律体现在具体的图形之中.(1)、我们在学习许多代数公式时,可以用几何图形来推理,观察下列图形,找出可以推出的代数公式,(下面各图形均满足推导各公式的条件,只需填写对应公式的序号)
(1)、求m的值和点D的坐标;(2)、求DF所在直线的表达式;(3)、若该反比例函数图象与直线DF的另一交点为点G,求S△EFG.23. 《几何原本》是古希腊数学家欧几里得的一部不朽著作,是数学发展史的一个里程碑.在该书的第2幕“几何与代数”部分,记载了很多利用几何图形来论证的代数结论,利用几何给人以强烈印象将抽象的逻辑规律体现在具体的图形之中.(1)、我们在学习许多代数公式时,可以用几何图形来推理,观察下列图形,找出可以推出的代数公式,(下面各图形均满足推导各公式的条件,只需填写对应公式的序号)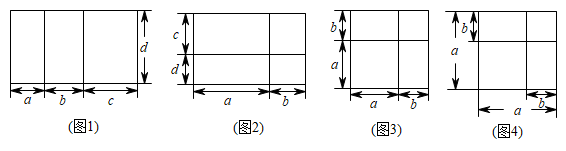
公式①:
公式②:
公式③:
公式④:
图1对应公式 , 图2对应公式 , 图3对应公式 , 图4对应公式;
(2)、《几何原本》中记载了一种利用几何图形证明平方差公式的方法,如图5,请写出证明过程;(已知图中各四边形均为矩形)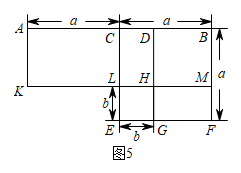 (3)、如图6,在等腰直角三角形ABC中, , D为BC的中点,E为边AC上任意一点(不与端点重合),过点E作于点G,作F点H过点B作BF//AC交EG的延长线于点F.记△BFG与△CEG的面积之和为 , △ABD与△AEH的面积之和为.
(3)、如图6,在等腰直角三角形ABC中, , D为BC的中点,E为边AC上任意一点(不与端点重合),过点E作于点G,作F点H过点B作BF//AC交EG的延长线于点F.记△BFG与△CEG的面积之和为 , △ABD与△AEH的面积之和为.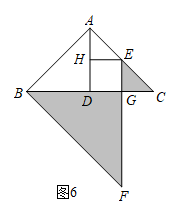
①若E为边AC的中点,则的值为 ▲ ;
②若E不为边AC的中点时,试问①中的结论是否仍成立?若成立,写出证明过程;若不成立,请说明理由.
24. 如图: (1)、【问题初探】
(1)、【问题初探】如图1,中, , , 点D是上一点,连接 , 以为一边作 , 使 , , 连接 , 与的数量关系 , 位置关系 .
(2)、【类比再探】如图2,中, , , 点M是上一点,点D是上一点,连接 , 以为一边作 , 使 , , 连接 , 求的度数.
(3)、【方法迁移】如图3,中, , , , 点M是中点,点D是上一点且 , 连接 , 以为一边作 , 使 , , 连接 , 求的长.