浙教版备考2023年中考数学一轮复习53.等边三角形的性质与判定
试卷更新日期:2022-12-31 类型:一轮复习
一、单选题(每题3分,共30分)
-
1. 下列关于等边三角形的描述不正确的是( )A、是轴对称图形 B、对称轴的交点是其重心 C、是中心对称图形 D、绕重心顺时针旋转120°能与自身重合2. 如图,在中, , , 是边的中点,是边上一点,若平分的周长,则的长为( )
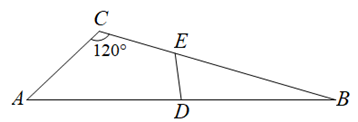 A、 B、 C、 D、3. 如图,直线 , 等边三角形的顶点在直线上, , 则的度数为( )
A、 B、 C、 D、3. 如图,直线 , 等边三角形的顶点在直线上, , 则的度数为( )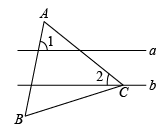 A、 B、 C、 D、4. 如图,等边、等边的边长分别为3和2.开始时点A与点D重合,在上,在上,沿向右平移,当点D到达点B时停止.在此过程中,设、重合部分的面积为y,移动的距离为x,则y与x的函数图象大致为( )
A、 B、 C、 D、4. 如图,等边、等边的边长分别为3和2.开始时点A与点D重合,在上,在上,沿向右平移,当点D到达点B时停止.在此过程中,设、重合部分的面积为y,移动的距离为x,则y与x的函数图象大致为( ) A、
A、 B、
B、 C、
C、 D、
D、 5. 如图,在等边中,为中点,点 , 分别为 , 上的点, , , 在上有一动点 , 则的最小值为( )
5. 如图,在等边中,为中点,点 , 分别为 , 上的点, , , 在上有一动点 , 则的最小值为( ) A、7 B、8 C、9 D、106. 如图,P是等边的边AC的中点,E为边延长线上一点, , 则的度数为( )
A、7 B、8 C、9 D、106. 如图,P是等边的边AC的中点,E为边延长线上一点, , 则的度数为( ) A、20° B、25° C、30° D、35°7. 如图,是等边三角形,过边上的点作的垂线交于点 , 作交于点 , 作交于点 , , 相交于点若 , , 则的长为( )
A、20° B、25° C、30° D、35°7. 如图,是等边三角形,过边上的点作的垂线交于点 , 作交于点 , 作交于点 , , 相交于点若 , , 则的长为( )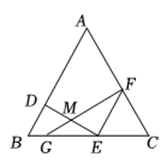 A、7 B、7.5 C、8 D、8.58. 一辆汽车沿A地北偏东50方向行驶6千米到达B地,再沿B地南偏东10°方向行驶6千米到达C地,则此时A、C两地相距( )千米。A、12 B、 C、6 D、39. 如图,点E是等边三角形△ABC边AC的中点,点D是直线BC上一动点,连接ED,并绕点E逆时针旋转90°,得到线段EF,连接DF.若运动过程中AF的最小值为 , 则AB的值为( )
A、7 B、7.5 C、8 D、8.58. 一辆汽车沿A地北偏东50方向行驶6千米到达B地,再沿B地南偏东10°方向行驶6千米到达C地,则此时A、C两地相距( )千米。A、12 B、 C、6 D、39. 如图,点E是等边三角形△ABC边AC的中点,点D是直线BC上一动点,连接ED,并绕点E逆时针旋转90°,得到线段EF,连接DF.若运动过程中AF的最小值为 , 则AB的值为( ) A、2 B、 C、 D、410. 如图,等边中,、分别为、边上的点, , 连接、交于点 , 、的平分线交于边上的点 , 与交于点 , 连接下列说法:≌;;;;其中正确的说法有( )
A、2 B、 C、 D、410. 如图,等边中,、分别为、边上的点, , 连接、交于点 , 、的平分线交于边上的点 , 与交于点 , 连接下列说法:≌;;;;其中正确的说法有( )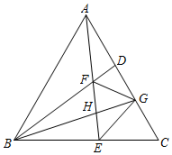 A、4个 B、3个 C、2个 D、1个
A、4个 B、3个 C、2个 D、1个二、填空题(每题4分,共24分)
-
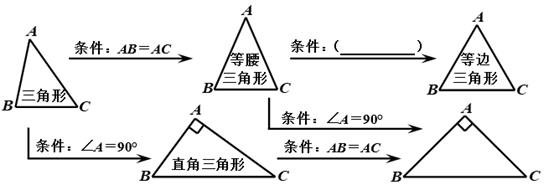
11. 小曹同学复习时将几种三角形的关系整理如图,请帮他在括号内填上一个适当的条件 .
 12. 如图,等边中, , 点E为高上的一动点,以为边作等边 , 连接 , , 则 , 的最小值为 .
12. 如图,等边中, , 点E为高上的一动点,以为边作等边 , 连接 , , 则 , 的最小值为 . 13. 跳棋是一项传统的智力游戏.如图是一副跳棋棋盘的示意图,它可以看作是由全等的等边三角形和等边三角形组合而成,它们重叠部分的图形为正六边形.若厘米,则这个正六边形的周长为厘米.
13. 跳棋是一项传统的智力游戏.如图是一副跳棋棋盘的示意图,它可以看作是由全等的等边三角形和等边三角形组合而成,它们重叠部分的图形为正六边形.若厘米,则这个正六边形的周长为厘米.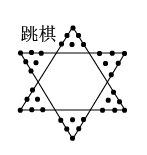
 14. 等边三角形ABC中,D是边BC上的一点,BD=2CD,以AD为边作等边三角形ADE,连接CE.若CE=2,则等边三角形ABC的边长为 .15. 如图,已知图①是一块边长为1,周长记为C1的等边三角形卡纸,把图①的卡纸剪去一个边长为的等边三角形纸板后得到图②,然后沿同一底边再剪去一个边长为的等边三角形后得到图③,依次剪去一个边长为、、…的等边三角形后,得到图④、⑤、⑥、…,记图n(n≥3)中的卡纸的周长为Cn , 则Cn-Cn-1= .
14. 等边三角形ABC中,D是边BC上的一点,BD=2CD,以AD为边作等边三角形ADE,连接CE.若CE=2,则等边三角形ABC的边长为 .15. 如图,已知图①是一块边长为1,周长记为C1的等边三角形卡纸,把图①的卡纸剪去一个边长为的等边三角形纸板后得到图②,然后沿同一底边再剪去一个边长为的等边三角形后得到图③,依次剪去一个边长为、、…的等边三角形后,得到图④、⑤、⑥、…,记图n(n≥3)中的卡纸的周长为Cn , 则Cn-Cn-1= . 16. 如图,等边△ABC内有一点O,OA=3,OB=4,OC=5,以点B为旋转中心将BO逆时针旋转60°得到线段 , 连接 , 下列结论:①可以看成是△BOC绕点B逆时针旋转60°得到的;②点O与的距离为5;③∠AOB=150°;④S四边形AOBO′=6+4;⑤=6+ . 其中正确的结论有 . (填正确序号)
16. 如图,等边△ABC内有一点O,OA=3,OB=4,OC=5,以点B为旋转中心将BO逆时针旋转60°得到线段 , 连接 , 下列结论:①可以看成是△BOC绕点B逆时针旋转60°得到的;②点O与的距离为5;③∠AOB=150°;④S四边形AOBO′=6+4;⑤=6+ . 其中正确的结论有 . (填正确序号)
三、解答题(共8题,共66分)
-
17. 如图,△ 是等边三角形, 在直线 上, .

求证: .
18. 如图,边长为6的等边三角形ABC内接于⊙O,点D为AC上的动点(点A、C除外),BD的延长线交⊙O于点E,连接CE.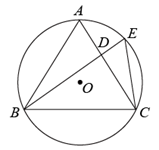 (1)、求证 ;(2)、当 时,求CE的长.19. 如图,点D在等边的外部,E为边上的一点, , 交于点F, .
(1)、求证 ;(2)、当 时,求CE的长.19. 如图,点D在等边的外部,E为边上的一点, , 交于点F, .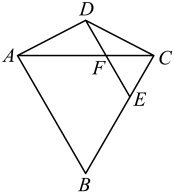 (1)、判断的形状,并说明理由;(2)、若 , , 求的长.20. 如图1,△ABC是等边三角形,点D在△ABC的内部,连接AD,将线段AD绕点A按逆时针方向旋转60°,得到线段AE,连接BD,DE,CE.
(1)、判断的形状,并说明理由;(2)、若 , , 求的长.20. 如图1,△ABC是等边三角形,点D在△ABC的内部,连接AD,将线段AD绕点A按逆时针方向旋转60°,得到线段AE,连接BD,DE,CE. (1)、判断线段BD与CE的数量关系并给出证明;(2)、延长ED交直线BC于点F.
(1)、判断线段BD与CE的数量关系并给出证明;(2)、延长ED交直线BC于点F.①如图2,当点F与点B重合时,直接用等式表示线段AE,BE和CE的数量关系为 ▲ ;
②如图3,当点F为线段BC中点,且ED=EC时,猜想∠BAD的度数,并说明理由.
21. 和都是等边三角形. (1)、将绕点A旋转到图①的位置时,连接BD,CE并延长相交于点P(点P与点A重合),有(或)成立;请证明.(2)、将绕点A旋转到图②的位置时,连接BD,CE相交于点P,连接PA,猜想线段PA、PB、PC之间有怎样的数量关系?并加以证明;(3)、将绕点A旋转到图③的位置时,连接BD,CE相交于点P,连接PA,猜想线段PA、PB、PC之间有怎样的数量关系?直接写出结论,不需要证明.22. 如图,在中, , , . 动点从点出发,以的速度沿边向终点匀速运动.以为一边作 , 另一边与折线相交于点 , 以为边作菱形 , 点在线段上.设点的运动时间为 , 菱形与重叠部分图形的面积为 .
(1)、将绕点A旋转到图①的位置时,连接BD,CE并延长相交于点P(点P与点A重合),有(或)成立;请证明.(2)、将绕点A旋转到图②的位置时,连接BD,CE相交于点P,连接PA,猜想线段PA、PB、PC之间有怎样的数量关系?并加以证明;(3)、将绕点A旋转到图③的位置时,连接BD,CE相交于点P,连接PA,猜想线段PA、PB、PC之间有怎样的数量关系?直接写出结论,不需要证明.22. 如图,在中, , , . 动点从点出发,以的速度沿边向终点匀速运动.以为一边作 , 另一边与折线相交于点 , 以为边作菱形 , 点在线段上.设点的运动时间为 , 菱形与重叠部分图形的面积为 .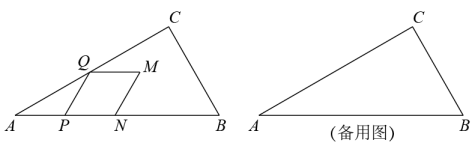 (1)、当点在边上时,的长为;(用含的代数式表示)(2)、当点落在边上时,求的值;(3)、求关于的函数解析式,并写出自变量的取值范围.23. 如图1,点P,Q分别是边长为4 cm的等边△ABC边AB,BC上的动点,点P从顶点A,点Q从顶点B同时出发,都以1 cm/s的速度分别向B,C运动.
(1)、当点在边上时,的长为;(用含的代数式表示)(2)、当点落在边上时,求的值;(3)、求关于的函数解析式,并写出自变量的取值范围.23. 如图1,点P,Q分别是边长为4 cm的等边△ABC边AB,BC上的动点,点P从顶点A,点Q从顶点B同时出发,都以1 cm/s的速度分别向B,C运动. (1)、连接AQ,CP交于点M,则P,Q运动的过程中,∠CMQ的大小变化吗?若变化,说明理由;若不变,求出它的度数;(2)、何时△PBQ是直角三角形?(3)、如图2,若点P,Q在运动到终点后继续在射线 AB,BC上运动,直线AQ,CP交于点M,则∠CMQ的度数为.24. 解答题(1)、如图1,和都是等边三角形,连接、 , 求证,;
(1)、连接AQ,CP交于点M,则P,Q运动的过程中,∠CMQ的大小变化吗?若变化,说明理由;若不变,求出它的度数;(2)、何时△PBQ是直角三角形?(3)、如图2,若点P,Q在运动到终点后继续在射线 AB,BC上运动,直线AQ,CP交于点M,则∠CMQ的度数为.24. 解答题(1)、如图1,和都是等边三角形,连接、 , 求证,;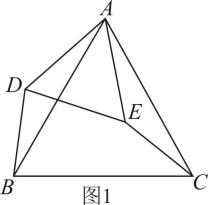 (2)、[类比探究]
(2)、[类比探究]如图2,和都是等腰直角三角形, , 连接 . 求的值.
 (3)、[拓展提升]
(3)、[拓展提升]如图3,和都是直角三角形, , . 连接 , 延长交于点F,连接 . 若恰好等于 , 请直接写出此时之间的数量关系.
