浙教版备考2023年中考数学一轮复习52.等腰三角形的性质与判定

试卷更新日期：2022-12-31 类型：一轮复习

进入出卷网下载

一、单选题（每题3分，共30分）

1. 等腰三角形的一个外角是70°，则它的顶角的度数为（）

A、70° B、70°或40° C、110° D、110°或40°

查看试题解析
2. 如图，在等腰三角形ABC中，BD为∠ABC的平分线，∠A=36°，AB=AC=a，BC=b，则CD=（）

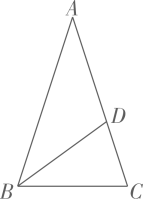A、 $\frac{a + b}{2}$ B、 $\frac{a - b}{2}$ C、a-b D、b-a

查看试题解析
3. △ABC 中，AB＝AC，过其中一个顶点的直线可以把这个三角形分成另外两个等腰三角形，则∠BAC（）

A、36°，90°， $\frac{180 °}{7}$ ， 108° B、36°，72°， $\frac{180 °}{7}$ ，90° C、90°，72°，108°， $\frac{180 °}{7}$ D、36°，90°，108°， $\frac{108 °}{7}$

查看试题解析
4. 如图，在 $△ A B C$ 中， $A B = A C$ ， $∠ B A C = 24 °$ ，延长 $B C$ 到点 $D$ ，使 $C D = A C$ ，连接 $A D$ ，则 $∠ D$ 的度数（）

A、 $39 °$ B、 $40 °$ C、 $49 °$ D、 $51 °$

查看试题解析
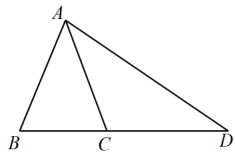5. 在平面直角坐标系中，点A在第一象限，点P在x轴上，若以P，O，A为顶点的三角形是等腰三角形，则满足条件的点P的个数是（）

A、2 B、3 C、4 D、2或4

查看试题解析
6. 将一平板保护套展开放置在水平桌面上，其侧面示意图如图所示，若 $∠ A B C = ∠ A C B$ ， $A B = 10 c m$ ，则 $A C$ 的长为（）

A、 $10 c m$ B、 $11 c m$ C、 $12 c m$ D、 $13 c m$

查看试题解析
7. 习题课上，张老师和同学们一起探究一个问题：“如图，在 $△ A B C$ 中， $D 、 E$ 分别是 $A C 、 A B$ 上的点， $B D$ 与 $C E$ 相交于点 $O ， O B = O C$ ，添加下列哪个条件能判定 $△ A B C$ 是等腰三角形?"请你判断正确的条件应为（）

A、 $A E = B E$ B、 $B E = C D$ C、 $∠ B E O = ∠ C D O$ D、 $∠ B E O = ∠ B O E$

查看试题解析
8. 如图，在△ABC 中，AB＝AC，∠A＝36°，BD、CE 分别是∠ABC、∠ACB 的平分线，则图中的等腰三角形有（）

A、5 个 B、6 个 C、7 个 D、8 个

查看试题解析
9. 如图，在等腰 $△ A B C$ 中， $∠ B A C = 120 °$ ， BC= $6 \sqrt{3}$ ， $⊙ O$ 同时与边 $B A$ 的延长线、射线 $A C$ 相切， $⊙ O$ 的半径为3．将 $△ A B C$ 绕点 $A$ 按顺时针方向旋转 $α (0 ° < α \leq 360 °)$ ， $B$ 、 $C$ 的对应点分别为 $B^{'}$ 、 $C^{'}$ ，在旋转的过程中边 $B^{'} C^{'}$ 所在直线与 $⊙ O$ 相切的次数为（）

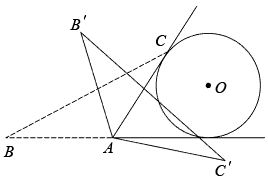A、1 B、2 C、3 D、4

查看试题解析
10. 如图，将一个等腰直角三角形△ABC按如图方式折叠，若DE=a，DC=b，下列四个结论：①DC′平分∠BDE；②BC长为2a+b；③△BDC′是等腰三角形；④△CED的周长等于BC的长.其中，正确的是（）

A、①②④ B、②③④ C、②③ D、②④

查看试题解析

二、填空题（每题4分，共24分）

11. 若（a﹣3）²+ $\sqrt{b - 5}$ =0，则以a、b为边长的等腰三角形的周长为.

查看试题解析
12. 矩形ABCD中， $A B = 8$ ， $A D = 7$ ，点E在AB边上， $A E = 5$ ．若点P是矩形ABCD边上一点，且与点A，E构成以AE为腰的等腰三角形，则等腰三角形AEP的底边长是．

查看试题解析
13. 如图，在 $△ A B C$ 中， $A B = A C$ ， $A D ⊥ B C$ 于点 $D$ ，若 $B C = 6$ ，则 $C D =$ .

查看试题解析
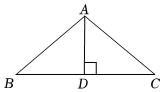14. 过等腰三角形顶角顶点的一条直线，将该等腰三角形分成的两个三角形均为等腰三角形，则原等腰三角形的底角度数为．

查看试题解析
15. 如图，在ΔABC中，∠A=36°，AB=AC，BD平分∠ABC，则图中等腰三角形的个数是

查看试题解析
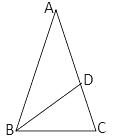16. 俊俊和霞霞共同合作将一张长为 $\sqrt{2}$ ，宽为1的矩形纸片进行裁剪（共裁剪三次），裁剪出来的图形刚好是4个等腰三角形（无纸张剩余）．霞霞说：“有一个等腰三角形的腰长是1”；俊俊说：“有一个等腰三角形的腰长是 $\sqrt{2} - 1$ ”；那么另外两个等腰三角形的腰长可能是．

查看试题解析

三、解答题（共8题，共66分）

17. 如图，在长、宽分别为4和2的长方形的边上取8个标记点，它们连同4个顶点将长方形的周长等分，请在三条边上各取一个标记点，按要求画出所需三角形.

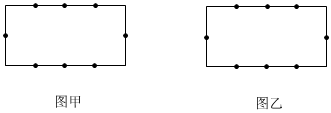(1)、在图甲中，画出等腰三角形，但不是直角三角形.

(2)、在图乙中，画出直角三角形，但不是等腰三角形.

查看试题解析
18. 如图，已知锐角三角形 $A B C$ 的两条高 $B E ， C D$ 相交于点O，且 $O B = O C$ ．请你判断 $△ A B C$ 的形状，并说明理由．

查看试题解析
19. 如图，在三角形ABC中，AB＝AC，∠C＝25°，点D在线段CA的延长线上，且DA＝AC，求∠ABD的度数.

查看试题解析
20. 如图，在 $△ A B C$ 中， $A B = A C$ ，以 $A B$ 为直径的⊙ $O$ 交 $B C$ 于点 $D$ ，交线段 $C A$ 的延长线于点 $E$ ，连接 $B E$ ．

(1)、求证： $B D = C D$ ；

(2)、若 $t a n C = \frac{1}{2}$ ， $B D = 4$ ，求 $A E$ ．

查看试题解析
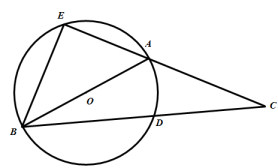21. 性质探究

(1)、如图①，在等腰三角形 $A B C$ 中， $∠ A C B = 120^{0}$ ，则底边 $A B$ 与腰 $A C$ 的长度之比为．

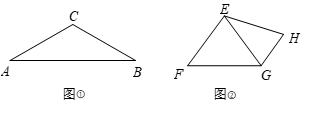(2)、理解运用
若顶角为120°的等腰三角形的周长为 $8 + 4 \sqrt{3}$ ，则它的面积为；

(3)、如图②，在四边形 $E F G H$ 中， $E F = E G = E H$ ．
①求证： $∠ E F G + ∠ E H G = ∠ F G H$ ；

②在边 $F G ， G H$ 上分别取中点 $M ， N$ ，连接 $M N$ ．若 $∠ F G H = 120^{0}$ ， $E F = 10$ ，直接写出线段 $M N$ 的长．

(4)、类比拓展
顶角为 $2 σ$ 的等腰三角形的底边与一腰的长度之比为（用含 $σ$ 的式子表示）．

查看试题解析
22. 如图，在平面直角坐标系中，平行四边形ABCD的边AB在x轴上，顶点D在y轴的正半轴上，M为BC的中点，OA、OB的长分别是一元二次方程 $x^{2} - 7 x + 12 = 0$ 的两个根 $(O A < O B)$ ， $t a n ∠ D A B = \frac{4}{3}$ ，动点P从点D出发以每秒1个单位长度的速度沿折线 $D C - C B$ 向点B运动，到达B点停止．设运动时间为t秒， $△ A P C$ 的面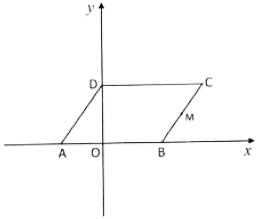积为S．

(1)、求点C的坐标；

(2)、求S关于t的函数关系式，并写出自变量t的取值范围；

(3)、在点P的运动过程中，是否存在点P，使 $△ C M P$ 是等腰三角形？若存在，请直接写出点P的坐标；若不存在，请说明理由．

查看试题解析
23. 概念学习
规定：如果一个三角形的三个角分别等于另一个三角形的三个角，那么称这两个三角形互为“等角三角形”.

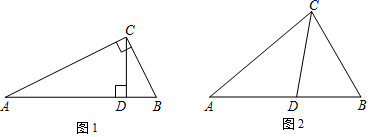
从三角形 $($ 不是等腰三角形 $)$ 一个顶点引出一条射线与对边相交，顶点与交点之间的线段把这个三角形分割成两个小三角形，如果分得的两个小三角形中一个为等腰三角形，另一个与原来三角形是“等角三角形”，我们把这条线段叫做这个三角形的“等角分割线”.

(1)、理解概念
如图1，在 $R t △ A B C$ 中， $∠ A C B = 90 °$ ， $C D ⊥ A B$ ，请写出图中两对“等角三角形”

(2)、概念应用
如图2，在 $△ A B C$ 中， $C D$ 为角平分线， $∠ A = 40 °$ ， $∠ B = 60 °$ .
求证： $C D$ 为 $△ A B C$ 的等角分割线.

(3)、在 $△ A B C$ 中， $∠ A = 42 °$ ， $C D$ 是 $△ A B C$ 的等角分割线，直接写出 $∠ A C B$ 的度数.

查看试题解析
24. 如图，已知 $△ A B C$ 中， $∠ B = 90 ° ， A B = 8 c m ， B C = 6 c m$ ， P、Q是 $△ A B C$ 边上的两个动点，其中点P从点A开始沿 $A \to B$ 方向运动，且速度为每秒1cm，点Q从点B开始沿 $B \to C \to A$ 方向运动，且速度为每秒2cm，它们同时出发，设出发的时间为t秒.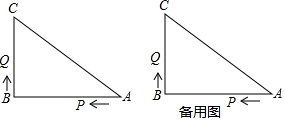

(1)、出发2秒后，求PQ的长；

(2)、当点Q在边BC上运动时，出发几秒钟， $△ P Q B$ 能形成等腰三角形？

(3)、当点Q在边CA上运动时，求能使 $△ B C Q$ 成为等腰三角形的运动时间（只要直接写出答案）.

查看试题解析