浙教版备考2023年中考数学一轮复习51.全等三角形的性质与判定
试卷更新日期:2022-12-31 类型:一轮复习
一、单选题(每题3分,共30分)
-
1. 下列各组图形中,属全等图形的是( )A、周长相等的两个等腰三角形 B、面积相等的两个长方形 C、面积相等的两个直角三角形 D、周长相等的两个圆2. 如图, , 点D在BC上,下列结论中不一定成立的是( )
 A、 B、 C、 D、3. 工人师傅常常利用角尺构造全等三角形的方法来平分一个角.如图,在 的两边 、 上分别在取 ,移动角尺,使角尺两边相同的刻度分别与点 、 重合,这时过角尺顶点 的射线 就是 的平分线.这里构造全等三角形的依据是( )
A、 B、 C、 D、3. 工人师傅常常利用角尺构造全等三角形的方法来平分一个角.如图,在 的两边 、 上分别在取 ,移动角尺,使角尺两边相同的刻度分别与点 、 重合,这时过角尺顶点 的射线 就是 的平分线.这里构造全等三角形的依据是( )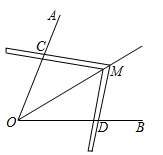 A、 B、 C、 D、4. 如图,E、F、G、H分别是矩形的边AB、BC、CD、AD上的点,AH=CF,AE=CG,∠EHF=60°,∠GHF=45°.若AH=2,AD=5+ . 则四边形EFGH的周长为( )
A、 B、 C、 D、4. 如图,E、F、G、H分别是矩形的边AB、BC、CD、AD上的点,AH=CF,AE=CG,∠EHF=60°,∠GHF=45°.若AH=2,AD=5+ . 则四边形EFGH的周长为( )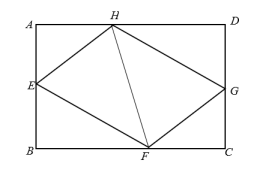 A、 B、 C、 D、5. 如图,在Rt△ABC中,∠A=90°,M为BC的中点,H为AB上一点,过点C作CG∥AB,交HM的延长线于点G,若AC=8,AB=6,则四边形ACGH周长的最小值是( )
A、 B、 C、 D、5. 如图,在Rt△ABC中,∠A=90°,M为BC的中点,H为AB上一点,过点C作CG∥AB,交HM的延长线于点G,若AC=8,AB=6,则四边形ACGH周长的最小值是( )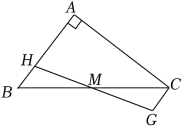 A、24 B、22 C、20 D、186. 如图,线段在平面直角坐标系内,A点坐标为 , 线段绕原点O逆时针旋转90°,得到线段 , 则点的坐标为( )
A、24 B、22 C、20 D、186. 如图,线段在平面直角坐标系内,A点坐标为 , 线段绕原点O逆时针旋转90°,得到线段 , 则点的坐标为( )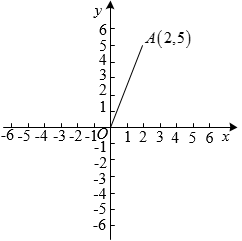 A、 B、 C、 D、7. 如图,△OAB的顶点O(0,0),顶点A,B分别在第一、四象限,且AB⊥x轴,若AB=6,OA=OB=5,则点A的坐标是( )
A、 B、 C、 D、7. 如图,△OAB的顶点O(0,0),顶点A,B分别在第一、四象限,且AB⊥x轴,若AB=6,OA=OB=5,则点A的坐标是( ) A、 B、 C、 D、8. 如图,在边长为3的正方形中,点是边上的点,且 , 过点作的垂线交正方形外角的平分线于点 , 交边于点 , 连接交边于点 , 则的长为( )
A、 B、 C、 D、8. 如图,在边长为3的正方形中,点是边上的点,且 , 过点作的垂线交正方形外角的平分线于点 , 交边于点 , 连接交边于点 , 则的长为( )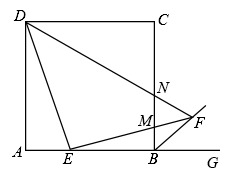 A、 B、 C、 D、19. 如图,在平行四边形 中, , 是锐角, 于点E,F是 的中点,连接 ;若 ,则 的长为( )
A、 B、 C、 D、19. 如图,在平行四边形 中, , 是锐角, 于点E,F是 的中点,连接 ;若 ,则 的长为( )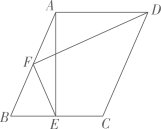 A、2 B、 C、 D、10. 题目:“如图,∠B=45°,BC=2,在射线BM上取一点A , 设AC=d , 若对于d的一个数值,只能作出唯一 一个△ABC , 求d的取值范围.”对于其答案,甲答: ,乙答:d=1.6,丙答: ,则正确的是( )
A、2 B、 C、 D、10. 题目:“如图,∠B=45°,BC=2,在射线BM上取一点A , 设AC=d , 若对于d的一个数值,只能作出唯一 一个△ABC , 求d的取值范围.”对于其答案,甲答: ,乙答:d=1.6,丙答: ,则正确的是( ) A、只有甲答的对 B、甲、丙答案合在一起才完整 C、甲、乙答案合在一起才完整 D、三人答案合在一起才完整
A、只有甲答的对 B、甲、丙答案合在一起才完整 C、甲、乙答案合在一起才完整 D、三人答案合在一起才完整二、填空题(每题4分,共24分)
-
11. 如图, , 相交于点 , , 要使≌ , 添加一个条件是 . (只写一个)
 12. 如图,AB⊥BC于点B,AB⊥AD于点A,点E是CD中点,若BC=5,AD=10,BE= , 则AB的长是 .
12. 如图,AB⊥BC于点B,AB⊥AD于点A,点E是CD中点,若BC=5,AD=10,BE= , 则AB的长是 . 13. 等边三角形ABC中,D是边BC上的一点,BD=2CD,以AD为边作等边三角形ADE,连接CE.若CE=2,则等边三角形ABC的边长为 .14. 如图,在边长为6的等边 中,点 , 分别是边 , 上的动点,且 ,连接 , 交于点 ,连接 ,则 的最小值为.
13. 等边三角形ABC中,D是边BC上的一点,BD=2CD,以AD为边作等边三角形ADE,连接CE.若CE=2,则等边三角形ABC的边长为 .14. 如图,在边长为6的等边 中,点 , 分别是边 , 上的动点,且 ,连接 , 交于点 ,连接 ,则 的最小值为. 15. 如图,是等腰直角三角形,直角顶点与坐标原点重合,若点B在反比例函数的图象上,则经过点A的反比例函数表达式为 .
15. 如图,是等腰直角三角形,直角顶点与坐标原点重合,若点B在反比例函数的图象上,则经过点A的反比例函数表达式为 .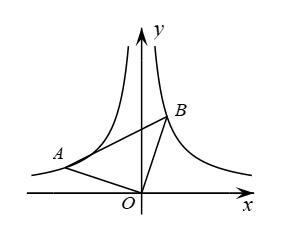 16. 如图,与都是等边三角形,和相交于点 , 连接下面结论中,;;不是的平分线;所有正确结论的序号是 .
16. 如图,与都是等边三角形,和相交于点 , 连接下面结论中,;;不是的平分线;所有正确结论的序号是 .
三、解答题(共8题,共66分)
-
17. 如图,在10×10的正方形网格中,小正方形的顶点称为格点,顶点均在格点上的图形称为格点图形,图中△ABC为格点三角形.请按要求作图,不需证明.
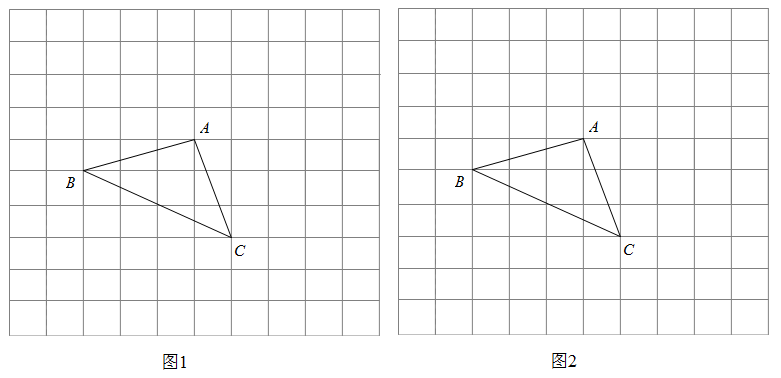 (1)、在图1中,作出与△ABC全等的所有格点三角形,要求所作格点三角形与△ABC有一条公共边,且不与△ABC重叠;(2)、在图2中,作出以BC为对角线的所有格点菱形.18. 已知:如图,在菱形ABCD中,E,F是对角线AC上两点,连接DE,DF,∠ADF=∠CDE.求证:AE=CF.
(1)、在图1中,作出与△ABC全等的所有格点三角形,要求所作格点三角形与△ABC有一条公共边,且不与△ABC重叠;(2)、在图2中,作出以BC为对角线的所有格点菱形.18. 已知:如图,在菱形ABCD中,E,F是对角线AC上两点,连接DE,DF,∠ADF=∠CDE.求证:AE=CF.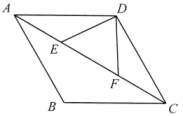 19. 已知:如图,点、、、在一条直线上,且 , , .求证:.
19. 已知:如图,点、、、在一条直线上,且 , , .求证:.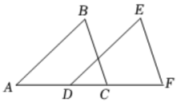 20. 如图,▱ABCD中,E为BC边的中点,连接AE并延长交DC的延长线于点F,延长EC至点G,使CG=CE,连接DG、DE、FG.
20. 如图,▱ABCD中,E为BC边的中点,连接AE并延长交DC的延长线于点F,延长EC至点G,使CG=CE,连接DG、DE、FG.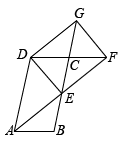 (1)、求证:△ABE≌△FCE;(2)、若AD=2AB,求证:四边形DEFG是矩形.21. 如图,点 , , , 在同一条直线上, , 有下列三个条件: , , .
(1)、求证:△ABE≌△FCE;(2)、若AD=2AB,求证:四边形DEFG是矩形.21. 如图,点 , , , 在同一条直线上, , 有下列三个条件: , , .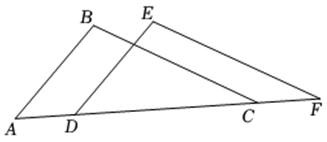 (1)、请在上述三个条件中选取一个条件,使得 ≌ .
(1)、请在上述三个条件中选取一个条件,使得 ≌ .你选取的条件为 ( 填写序号 ) ( 只需选一个条件,多选不得分 ),你判定 ≌ 的依据是 (填“ ”或“ ”或“ ”或“ ”);
(2)、利用 的结论 ≌ 求证: .22.(1)、启迪中学计划为七年级学生暑期军训配备如图1所示的折叠凳,这样设计的折叠凳坐着舒适、稳定.这种设计所运用的数学原理是;(2)、图2是折叠凳撑开后的侧面示意图(木条等材料宽度忽略不计),其中凳腿AB和CD的长相等,O是它们的中点,为了使折叠凳坐着舒适,厂家将撑开后的折叠凳宽度AD设计为40cm,则由以上信息可推得CB的长度是多少?请说明理由.
 23. 【思维探究】如图1,在四边形ABCD中,∠BAD=60°,∠BCD=120°,AB=AD,连接AC.求证:BC+CD=AC.
23. 【思维探究】如图1,在四边形ABCD中,∠BAD=60°,∠BCD=120°,AB=AD,连接AC.求证:BC+CD=AC.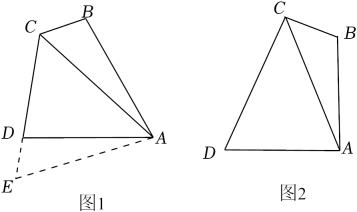 (1)、小明的思路是:延长CD到点E,使DE=BC,连接AE.根据∠BAD+∠BCD=180°,推得∠B+∠ADC=180°,从而得到∠B=∠ADE,然后证明ADE≌ABC,从而可证BC+CD=AC,请你帮助小明写出完整的证明过程.(2)、【思维延伸】如图2,四边形ABCD中,∠BAD=∠BCD=90°,AB=AD,连接AC,猜想BC,CD,AC之间的数量关系,并说明理由.(3)、【思维拓展】在四边形ABCD中,∠BAD=∠BCD=90°,AB=AD= , AC与BD相交于点O.若四边形ABCD中有一个内角是75°,请直接写出线段OD的长.24. 为提高耕地灌溉效率,小明的爸妈准备在耕地、、、四个位置安装四个自动喷酒装置(如图1所示),、、、四点恰好在边长为50米的正方形的四个顶点上,为了用水管将四个自动喷洒装置相互连通,爸妈设计了如下两个水管铺设方案(各图中实线为铺设的水管).
(1)、小明的思路是:延长CD到点E,使DE=BC,连接AE.根据∠BAD+∠BCD=180°,推得∠B+∠ADC=180°,从而得到∠B=∠ADE,然后证明ADE≌ABC,从而可证BC+CD=AC,请你帮助小明写出完整的证明过程.(2)、【思维延伸】如图2,四边形ABCD中,∠BAD=∠BCD=90°,AB=AD,连接AC,猜想BC,CD,AC之间的数量关系,并说明理由.(3)、【思维拓展】在四边形ABCD中,∠BAD=∠BCD=90°,AB=AD= , AC与BD相交于点O.若四边形ABCD中有一个内角是75°,请直接写出线段OD的长.24. 为提高耕地灌溉效率,小明的爸妈准备在耕地、、、四个位置安装四个自动喷酒装置(如图1所示),、、、四点恰好在边长为50米的正方形的四个顶点上,为了用水管将四个自动喷洒装置相互连通,爸妈设计了如下两个水管铺设方案(各图中实线为铺设的水管).方案一:如图2所示,沿正方形的三边铺设水管;
方案二:如图3所示,沿正方形的两条对角线铺设水管.
 (1)、请通过计算说明上述两方案中哪个方案铺设水管的总长度更短:(2)、小明看了爸妈的方案后,根据“蜂集原理”重新设计了一个方案(如图4所示),
(1)、请通过计算说明上述两方案中哪个方案铺设水管的总长度更短:(2)、小明看了爸妈的方案后,根据“蜂集原理”重新设计了一个方案(如图4所示),满足 , , 、请将小明的方案与爸妈的方案比较,判断谁的方案中铺设水管的总长度更短,并说明理由.(参考数据: , )