浙教版备考2023年中考数学一轮复习50.角平分线与线段垂直平分线
试卷更新日期:2022-12-31 类型:一轮复习
一、单选题(每题3分,共30分)
-
1. 下列说法正确的是( )A、相等的角是对顶角 B、对角线相等的四边形是矩形 C、三角形的外心是它的三条角平分线的交点 D、线段垂直平分线上的点到线段两端的距离相等2. 如图所示,在中,按下列步骤作图:
第一步:在上分别截取 , 使;
第二步:分别以点D和点E为圆心、适当长(大于的一半)为半径作圆弧,两弧交于点F;
第三步:作射线交于点M;
第四步:过点M作于点N.
下列结论一定成立的是( )
 A、 B、 C、 D、3. 如图,是求作线段AB中点的作图痕迹,则下列结论不一定成立的是( )
A、 B、 C、 D、3. 如图,是求作线段AB中点的作图痕迹,则下列结论不一定成立的是( ) A、∠B=45° B、AE=EB C、AC=BC D、AB⊥CD4. 如图,在△ABC中,BD平分∠ABC,以点A为圆心,以任意长为半径画弧交射线AB,AC于两点,分别以这两点为圆心,以适当的定长为半径画弧,两弧交于点E,作射线AE,交BD于点I,连接CI,以下说法错误的是( )
A、∠B=45° B、AE=EB C、AC=BC D、AB⊥CD4. 如图,在△ABC中,BD平分∠ABC,以点A为圆心,以任意长为半径画弧交射线AB,AC于两点,分别以这两点为圆心,以适当的定长为半径画弧,两弧交于点E,作射线AE,交BD于点I,连接CI,以下说法错误的是( )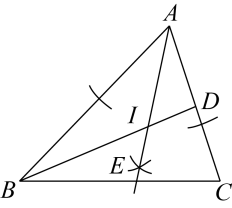 A、I到AB,AC边的距离相等 B、CI平分∠ACB C、I是△ABC的内心 D、I到A,B,C三点的距离相等5. 如图,∠MON=60°,以点O为圆心,适当长为半径画弧,交OM于点A,交ON于点B;分别以点A,B为圆心,大于AB的长为半径画弧,两弧在∠MON的内部相交于点P,画射线OP;连接AB,AP,BP,过点P作PE⊥OM于点E,PF⊥ON于点F.则以下结论错误的是( )
A、I到AB,AC边的距离相等 B、CI平分∠ACB C、I是△ABC的内心 D、I到A,B,C三点的距离相等5. 如图,∠MON=60°,以点O为圆心,适当长为半径画弧,交OM于点A,交ON于点B;分别以点A,B为圆心,大于AB的长为半径画弧,两弧在∠MON的内部相交于点P,画射线OP;连接AB,AP,BP,过点P作PE⊥OM于点E,PF⊥ON于点F.则以下结论错误的是( ) A、△AOB是等边三角形 B、PE=PF C、△PAE≌△PBF D、四边形OAPB是菱形6. 如图,在中, , 分别以点A和点C为圆心,大于的长为半径作弧,两弧相交于M,N两点,作直线 , 直线与相交于点D,连接 , 若 , 则的长是( )
A、△AOB是等边三角形 B、PE=PF C、△PAE≌△PBF D、四边形OAPB是菱形6. 如图,在中, , 分别以点A和点C为圆心,大于的长为半径作弧,两弧相交于M,N两点,作直线 , 直线与相交于点D,连接 , 若 , 则的长是( )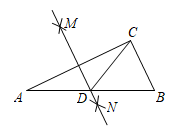 A、6 B、3 C、1.5 D、17. 如图,中,若 , , 根据图中尺规作图的痕迹推断,以下结论错误的是( )
A、6 B、3 C、1.5 D、17. 如图,中,若 , , 根据图中尺规作图的痕迹推断,以下结论错误的是( ) A、 B、 C、 D、8. 如图,在中,根据尺规作图痕迹,下列说法不一定正确的是( )
A、 B、 C、 D、8. 如图,在中,根据尺规作图痕迹,下列说法不一定正确的是( ) A、 B、 C、 D、9. 如图,在 中, 是 的角平分线,过点D分别作 ,垂足分别是点E,F,则下列结论错误的是( )
A、 B、 C、 D、9. 如图,在 中, 是 的角平分线,过点D分别作 ,垂足分别是点E,F,则下列结论错误的是( )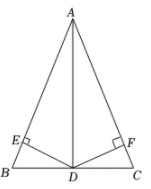 A、 B、 C、 D、10. 如图,线段是半圆O的直径。分别以点A和点O为圆心,大于的长为半径作弧,两弧交于M,N两点,作直线 , 交半圆O于点C,交于点E,连接 , , 若 , 则的长是( )
A、 B、 C、 D、10. 如图,线段是半圆O的直径。分别以点A和点O为圆心,大于的长为半径作弧,两弧交于M,N两点,作直线 , 交半圆O于点C,交于点E,连接 , , 若 , 则的长是( ) A、 B、4 C、6 D、
A、 B、4 C、6 D、二、填空题(每题4分,共24分)
-
11. 如图,依下列步骤尺规作图,并保留作图痕迹:
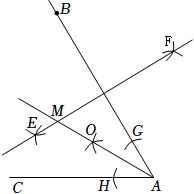
(1)分别以点A,B为圆心,大于AB的长为半径作弧,两弧相交于E,F两点,作直线EF;
(2)以点A为圆心,适当长为半径画弧,分别交AB,AC于点G,H,再分别以点G,H为圆心,大于GH的长为半径画弧,两弧在∠BAC的内部相交于点O,画射线AO,交直线EF于点M.
已知线段AB=6,∠BAC=60°,则点M到射线AC的距离为.12. 如图,在RtABC中,∠ACB=90°,AB=13,BC=12,分别以点B和点C为圆心、大于BC的长为半径作弧,两弧相交于E,F两点,作直线EF交AB于点D,连接CD,则ACD的周长是 .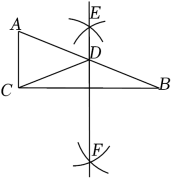 13. 如图,在Rt△ABC中,∠B=90°,AB=4,BC=8,分别以A,C为圆心,以大于AC的长为半径作弧,两弧相交于点P和点Q,直线PQ与AC交于点D,则AD的长为 .
13. 如图,在Rt△ABC中,∠B=90°,AB=4,BC=8,分别以A,C为圆心,以大于AC的长为半径作弧,两弧相交于点P和点Q,直线PQ与AC交于点D,则AD的长为 .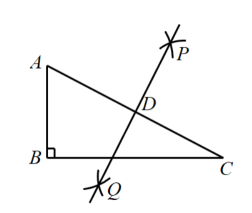 14. 如图.在 中, , .以点A为圆心,以任意长为半径作弧交AB,AC于D,E两点;分别以点D,E为圆心,以大于 长为半径作弧,在 内两弧相交于点P;作射线AP交BC于点F,过点F作 ,垂足用G.若 ,则 的周长等于cm.
14. 如图.在 中, , .以点A为圆心,以任意长为半径作弧交AB,AC于D,E两点;分别以点D,E为圆心,以大于 长为半径作弧,在 内两弧相交于点P;作射线AP交BC于点F,过点F作 ,垂足用G.若 ,则 的周长等于cm.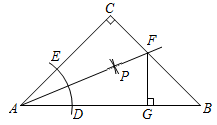 15. 如图,依据尺规作图的痕迹,求的度数°.
15. 如图,依据尺规作图的痕迹,求的度数°.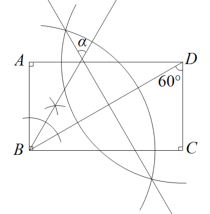 16. 如图所示,点在一块直角三角板上(其中),于点 , 于点 , 若 , 则度.
16. 如图所示,点在一块直角三角板上(其中),于点 , 于点 , 若 , 则度.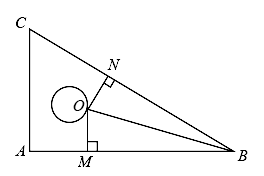
三、解答题(共8题,共66分)
-
17. 请仅用无刻度的直尺分别按下列要求画图(保留画图痕迹,不写画法).
 (1)、如图1,△ABC中,AB=AC,点D,E分别在AB,AC边上,且AD=AE,作出∠BAC的角平分线AF;(2)、如图2,四边形BCED中,BD=CE,∠B=∠C,M为BC边上一点,在BC边上作一点N,使CN=BM.18. 如图,在中,是的中点, , , 垂足分别是点、 , . 求证:平分 .
(1)、如图1,△ABC中,AB=AC,点D,E分别在AB,AC边上,且AD=AE,作出∠BAC的角平分线AF;(2)、如图2,四边形BCED中,BD=CE,∠B=∠C,M为BC边上一点,在BC边上作一点N,使CN=BM.18. 如图,在中,是的中点, , , 垂足分别是点、 , . 求证:平分 . 19. 如图,平分 , 点P是上任意一点,过点P向 , 作垂线段 , , 垂足分别为D,E,连接 . 求证:垂直平分 .
19. 如图,平分 , 点P是上任意一点,过点P向 , 作垂线段 , , 垂足分别为D,E,连接 . 求证:垂直平分 . 20. 如图,为了满足 , , 三个小区居民的体育锻炼需求,需要建立一个居民健身广场 , 要使健身广场到三个小区的距离相等,请你在图中作出健身广场的位置(要求:尺规作图,保留作图痕迹,不写作法).
20. 如图,为了满足 , , 三个小区居民的体育锻炼需求,需要建立一个居民健身广场 , 要使健身广场到三个小区的距离相等,请你在图中作出健身广场的位置(要求:尺规作图,保留作图痕迹,不写作法). 21. 教材呈现:如图是华师版八年级上册数学教材第96页的部分内容.
21. 教材呈现:如图是华师版八年级上册数学教材第96页的部分内容.
 (1)、定理证明:请根据教材中的分析,结合图①,写出“角平分线的性质定理”完整的证明过程.(2)、定理应用:
(1)、定理证明:请根据教材中的分析,结合图①,写出“角平分线的性质定理”完整的证明过程.(2)、定理应用:如图②,的周长是12,分别平分和 , 于点D,若 , 则的面积为 ▲ .
22. 如图,四边形中,ABDC, , 于点 .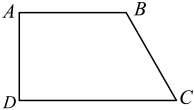 (1)、用尺规作的角平分线,交于点;(不写作法,保留作图痕迹)(2)、连接 . 求证:四边形是菱形.23. 如图,在等腰锐角三角形ABC中,AB=AC,过点B作BD⊥AC于D,延长BD交△ABC的外接圆于点E,过点A作AF⊥CE于F,AE,BC的延长线交于点G.
(1)、用尺规作的角平分线,交于点;(不写作法,保留作图痕迹)(2)、连接 . 求证:四边形是菱形.23. 如图,在等腰锐角三角形ABC中,AB=AC,过点B作BD⊥AC于D,延长BD交△ABC的外接圆于点E,过点A作AF⊥CE于F,AE,BC的延长线交于点G.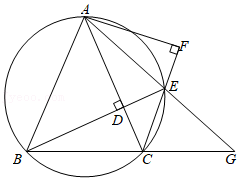 (1)、判断EA是否平分∠DEF,并说明理由;(2)、求证:①BD=CF;
(1)、判断EA是否平分∠DEF,并说明理由;(2)、求证:①BD=CF;②BD2=DE2+AE•EG.
24. 如图,在Rt△ACB中,∠C=90°, , , 点由出发沿方向向点匀速运动速度为;点由出发沿方向向点匀速运动,速度为;连接 . 若设运动的时间为 , 解答下列问题: (1)、当为何值时,点在垂直平分线上?(2)、当为何值时,△APQ为直角三角形?(3)、是否存在某一时刻 , 使线段恰好把Rt△ACB的面积平分?若存在,求出此时的值;若不存在,说明理由.
(1)、当为何值时,点在垂直平分线上?(2)、当为何值时,△APQ为直角三角形?(3)、是否存在某一时刻 , 使线段恰好把Rt△ACB的面积平分?若存在,求出此时的值;若不存在,说明理由.