浙教版备考2023年中考数学一轮复习48.作图——四边形与圆
试卷更新日期:2022-12-31 类型:一轮复习
一、作图-四边形
-
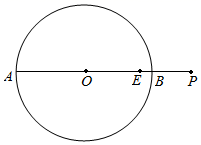
1. 如图,在中,用直尺和圆规作图,作图痕迹如图所示,AG交BC于点E.若AB=4,∠BAD=60°,则AE的长为( )
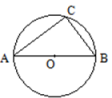
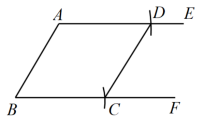
 A、6 B、2 C、4 D、82. 如图,已知▱的一组邻边 , , 用尺规作图作▱ , 下列4个作图中,作法与理论依据都正确的有几个( )
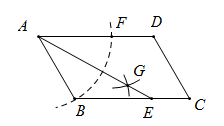
A、6 B、2 C、4 D、82. 如图,已知▱的一组邻边 , , 用尺规作图作▱ , 下列4个作图中,作法与理论依据都正确的有几个( )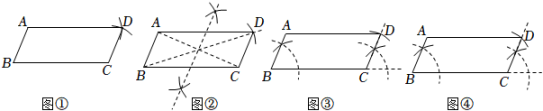 A、1个 B、2个 C、3个 D、4个3. 如图,矩形ABCD,作图痕迹,则下列结果说法错误的是( )
A、1个 B、2个 C、3个 D、4个3. 如图,矩形ABCD,作图痕迹,则下列结果说法错误的是( )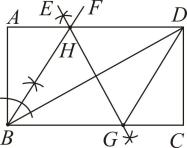 A、四边形BHDG是菱形 B、 C、若 , 则 D、DG平分4. 如图,四边形ABCD为矩形,依据尺规作图的痕迹,∠α与∠β的度数之间的关系为( )
A、四边形BHDG是菱形 B、 C、若 , 则 D、DG平分4. 如图,四边形ABCD为矩形,依据尺规作图的痕迹,∠α与∠β的度数之间的关系为( )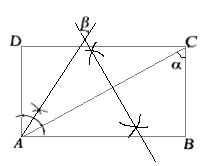 A、∠β= 180-∠α B、∠β=180°- C、∠β=90°-∠α D、∠β=90°-5. 如图,在中, . 作出点D,使四边形是矩形.(要求:尺规作图,不写作法,保留作图痕迹)
A、∠β= 180-∠α B、∠β=180°- C、∠β=90°-∠α D、∠β=90°-5. 如图,在中, . 作出点D,使四边形是矩形.(要求:尺规作图,不写作法,保留作图痕迹)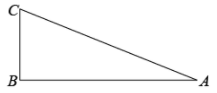 6. 如图为方格,每个小正方形的边长都为1.
6. 如图为方格,每个小正方形的边长都为1.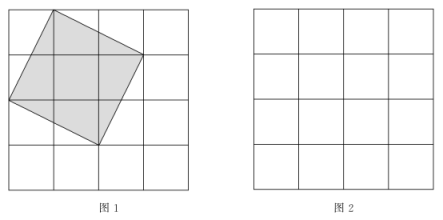 (1)、图1中阴影正方形的面积为 , 边长为;(2)、请在图2中画出一个与图1中阴影部分面积不相等的正方形,并求出所画正方形的边长.要求所画正方形满足以下条件:①正方形的边长为无理数 ②正方形的四个顶点均在网格格点处.7. 图①、图②均是的正方形网格,每个小正方形的边长均为1个单位长度,每个小正方形的顶点称为格点,点A、B、C均在格点上.在图①、图②给定网格中按要求作图,只用无刻度的直尺,保留适当的作图痕迹.
(1)、图1中阴影正方形的面积为 , 边长为;(2)、请在图2中画出一个与图1中阴影部分面积不相等的正方形,并求出所画正方形的边长.要求所画正方形满足以下条件:①正方形的边长为无理数 ②正方形的四个顶点均在网格格点处.7. 图①、图②均是的正方形网格,每个小正方形的边长均为1个单位长度,每个小正方形的顶点称为格点,点A、B、C均在格点上.在图①、图②给定网格中按要求作图,只用无刻度的直尺,保留适当的作图痕迹.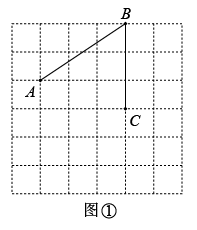
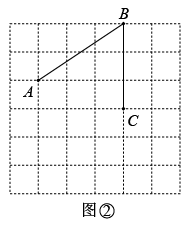 (1)、在图①中确定一个格点D,连接、 , 使四边形是平行四边形.(2)、先在图②中的线段上确定一点E,使最短,再在图②中确定一点F,连接、 , 使四边形为平行四边形.8. 已知四边形为矩形.点E是边的中点.请仅用无刻度的直尺完成下列作图,不写作法,保留作图痕迹.
(1)、在图①中确定一个格点D,连接、 , 使四边形是平行四边形.(2)、先在图②中的线段上确定一点E,使最短,再在图②中确定一点F,连接、 , 使四边形为平行四边形.8. 已知四边形为矩形.点E是边的中点.请仅用无刻度的直尺完成下列作图,不写作法,保留作图痕迹.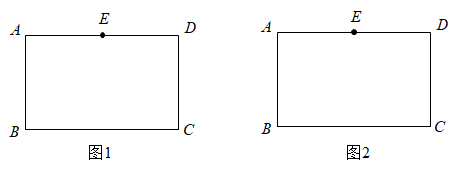 (1)、在图1中作出矩形的对称轴m,使;(2)、在图2中作出矩形的对称轴n:使.9. 【阅读材料】
(1)、在图1中作出矩形的对称轴m,使;(2)、在图2中作出矩形的对称轴n:使.9. 【阅读材料】老师的问题:
已知:如图, .
求作:菱形 , 使点C,D分别在上.
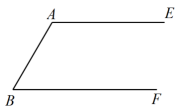
小明的作法:
(1)以A为圆心,长为半径画弧,交于点D;
(2)以B为圆心,长为半经画弧,交于点C;
(3)连接 .
四边形就是所求作的菱形,
【解答问题】
请根据材料中的信息,证明四边形是菱形.
10. 定义:在边长为1的小正方形方格纸中,把顶点落在方格交点上的线段、三角形、四边形分别称为格点线段、格点三角形、格点四边形,在的正方形网格中,若每一个小正方形的边长均为1,请仅用无刻度直尺按要求画图. (1)、在图①中画一个以为边画一个格点正方形 .(2)、在图②中画一个格点平行四边形 , 使平行四边形面积为6.(3)、在图③中画一个格点菱形 , 不是正方形(温馨提示:请画在答题卷相对应的图上)11. 如图,方格纸中每个小正方形的边长均为1,的顶点和线段的端点均在小正方形的顶点上.
(1)、在图①中画一个以为边画一个格点正方形 .(2)、在图②中画一个格点平行四边形 , 使平行四边形面积为6.(3)、在图③中画一个格点菱形 , 不是正方形(温馨提示:请画在答题卷相对应的图上)11. 如图,方格纸中每个小正方形的边长均为1,的顶点和线段的端点均在小正方形的顶点上.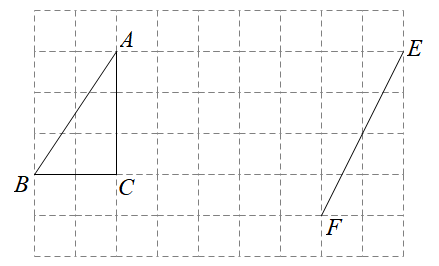
⑴在方格纸中面出 , 使与关于直线对称(点D在小正方形的顶点上);
⑵在方格纸中画出以线段为一边的平行四边形(点G,点H均在小正方形的顶点上),且平行四边形的面积为4.连接 , 请直接写出线段的长.
12. 下图是由边长为1的小等边三角形构成的网格,每个小等边三角形的顶点为格点,线段 的端点都在格点上.要求以 为边画一个平行四边形,且另外两个顶点在格点上.请在下面的网格图中画出4种不同的设计图形.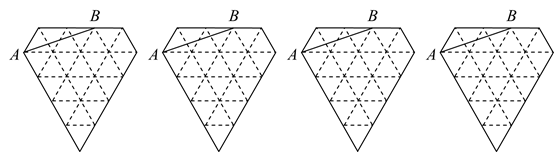 13. 如图是由小正方形组成的9×6网格,每个小正方形的顶点叫做格点.△ABC的三个顶点都是格点.仅用无刻度的直尺在给定网格中完成画图,画图过程用虚线表示.
13. 如图是由小正方形组成的9×6网格,每个小正方形的顶点叫做格点.△ABC的三个顶点都是格点.仅用无刻度的直尺在给定网格中完成画图,画图过程用虚线表示.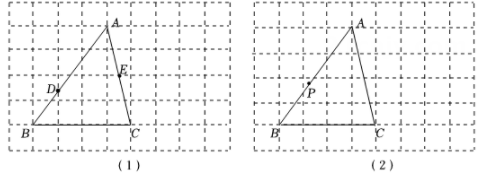 (1)、在图(1)中, , 分别是边 , 与网格线的交点.先将点绕点旋转得到点 , 画出点 , 再在上画点 , 使;(2)、在图(2)中,是边上一点,.先将绕点逆时针旋转 , 得到线段 , 画出线段 , 再画点 , 使 , 两点关于直线对称.14. Rt△ABC中,∠C=90°,AB=17,BC=8,矩形CDEF的另三个顶点D , E , F均在Rt△ABC的边上,且邻边之比为1:2,画出正确的图形,并直接写出矩形周长的值.
(1)、在图(1)中, , 分别是边 , 与网格线的交点.先将点绕点旋转得到点 , 画出点 , 再在上画点 , 使;(2)、在图(2)中,是边上一点,.先将绕点逆时针旋转 , 得到线段 , 画出线段 , 再画点 , 使 , 两点关于直线对称.14. Rt△ABC中,∠C=90°,AB=17,BC=8,矩形CDEF的另三个顶点D , E , F均在Rt△ABC的边上,且邻边之比为1:2,画出正确的图形,并直接写出矩形周长的值.二、作图-圆
-
15. 用尺规作图作三角形的外接圆时,用到了哪些基本作图( )A、作一条线段等于已知线段 B、作一个角等于已知角 C、作一个角的平分线 D、作一条线段的垂直平分线16. 根据下列圆规作图的痕迹,可以用直尺成功找到三角形外心的是 ( )A、
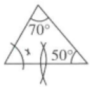 B、
B、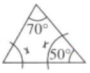 C、
C、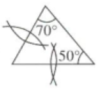 D、
D、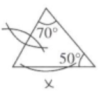 17. 在⊙O中按如下步骤作图:
17. 在⊙O中按如下步骤作图:⑴作⊙O的直径AD;
⑵以点D为圆心,DO长为半径画弧,交⊙O于B , C两点;
⑶连接DB , DC , AB , AC , BC .
根据以上作图过程及所作图形,下列四个结论中错误的是( )
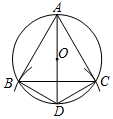 A、∠ABD=90° B、∠BAD=∠CBD C、AD⊥BC D、AC=2CD18. 如图,在6×6的正方形网格中,圆上A,B,C三点都在格点上,请按要求作出图中圆的圆心:①仅用无刻度直尺,且不能用直尺中的直角;②保留作图痕迹.
A、∠ABD=90° B、∠BAD=∠CBD C、AD⊥BC D、AC=2CD18. 如图,在6×6的正方形网格中,圆上A,B,C三点都在格点上,请按要求作出图中圆的圆心:①仅用无刻度直尺,且不能用直尺中的直角;②保留作图痕迹.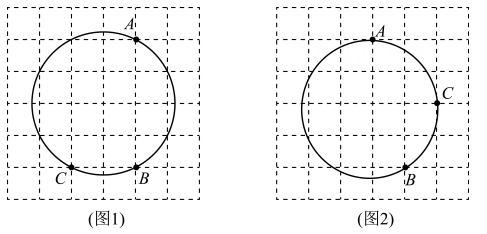 19. 如图,在中, .
19. 如图,在中, . (1)、实践与操作:利用尺规作的外接圆,圆心为点O(要求:尺规作图并保留作图痕迹,不写作法,标明字母).(2)、猜想与证明:若 , 试猜想线段 与半径r的数量关系,并加以证明.20. 如图,有一块破碎的圆形残片,请你用直尺和圆规找出它的圆心O.(保留作图痕迹).
(1)、实践与操作:利用尺规作的外接圆,圆心为点O(要求:尺规作图并保留作图痕迹,不写作法,标明字母).(2)、猜想与证明:若 , 试猜想线段 与半径r的数量关系,并加以证明.20. 如图,有一块破碎的圆形残片,请你用直尺和圆规找出它的圆心O.(保留作图痕迹). 21. 如图,在 中, ,AD为底边BC上的高,请用尺规作图法,作 的内切圆⊙O.(保留作图痕迹,不写作法)
21. 如图,在 中, ,AD为底边BC上的高,请用尺规作图法,作 的内切圆⊙O.(保留作图痕迹,不写作法)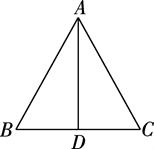 22. 如图,由小正方形构成的网格,经过 , , 三点,仅用无刻度的直尺按要求画图.保留作图痕迹
22. 如图,由小正方形构成的网格,经过 , , 三点,仅用无刻度的直尺按要求画图.保留作图痕迹 (1)、在图(1)中画弦的弦心距;(2)、在图(2)中的圆上找一点 , 使点是的中点.23. 如图,在中,已知.
(1)、在图(1)中画弦的弦心距;(2)、在图(2)中的圆上找一点 , 使点是的中点.23. 如图,在中,已知. (1)、尺规作图;画的外接圆(保留作图痕迹,不写画法),(2)、连接若 , 求扇形的面积.24. 如图,在每个小正方形的边长为1的网格中,圆上的点A,B,C及的一边上的点E,F均在格点上.
(1)、尺规作图;画的外接圆(保留作图痕迹,不写画法),(2)、连接若 , 求扇形的面积.24. 如图,在每个小正方形的边长为1的网格中,圆上的点A,B,C及的一边上的点E,F均在格点上.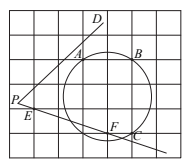 (1)、线段的长等于;(2)、若点M,N分别在射线上,满足且 . 请用无刻度的直尺,在如图所示的网格中,画出点M,N,并简要说明点M,N的位置是如何找到的(不要求证明) .25. 请仅用无刻度直尺完成以下作图.(保留画图痕迹,不写作法)
(1)、线段的长等于;(2)、若点M,N分别在射线上,满足且 . 请用无刻度的直尺,在如图所示的网格中,画出点M,N,并简要说明点M,N的位置是如何找到的(不要求证明) .25. 请仅用无刻度直尺完成以下作图.(保留画图痕迹,不写作法)已知四边形ABCD内接于 , 且已知 .
 (1)、在图1中已知 , 在上求作一个度数为30°的圆周角;(2)、在图2中,已知 , 在上求作一个度数为30°的圆周角.26. 如图,四边形ABCD是平行四边形,AD与圆相切,请在下图中,仅用无刻度的直尺按要求画图.
(1)、在图1中已知 , 在上求作一个度数为30°的圆周角;(2)、在图2中,已知 , 在上求作一个度数为30°的圆周角.26. 如图,四边形ABCD是平行四边形,AD与圆相切,请在下图中,仅用无刻度的直尺按要求画图.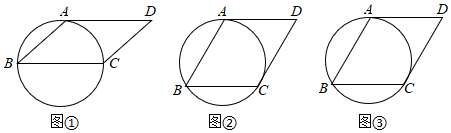
⑴如图①,若BC是圆的直径,画出平行四边形ABCD的边CD上的高;
⑵如图②,若CD与圆相切,画出平行四边形ABCD的边AD上的高CE;
⑶如图③,若CD与圆相切,画出平行四边形ABCD的边BC上的高AF .