浙教版备考2023年中考数学一轮复习48.作图——三角形
试卷更新日期:2022-12-31 类型:一轮复习
一、作图-三角形
-
1. 下列尺规作图,能判断AD是△ABC边上的中线的是( )A、
 B、
B、 C、
C、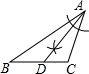 D、
D、 2. 根据下列已知条件,能唯一画出△ABC的是( )A、AB=3,BC=4,AC=8 B、∠C=90°,AB=6 C、AB=3,BC=3,∠C=30° D、∠A=60°,∠B=45°,AB=43. 用尺规作图作∠APB的平分线PQ,痕迹如图所示,则此作图的依据是( )
2. 根据下列已知条件,能唯一画出△ABC的是( )A、AB=3,BC=4,AC=8 B、∠C=90°,AB=6 C、AB=3,BC=3,∠C=30° D、∠A=60°,∠B=45°,AB=43. 用尺规作图作∠APB的平分线PQ,痕迹如图所示,则此作图的依据是( ) A、(ASA) B、(SSS) C、(SAS) D、(AAS)4. 如图,对三角形中的尺规作图描述正确的是( )
A、(ASA) B、(SSS) C、(SAS) D、(AAS)4. 如图,对三角形中的尺规作图描述正确的是( )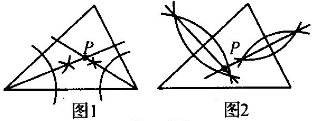 A、图1所求作的点P是三角形的内心,图2所求作的点P是三角形的重心 B、图1所求作的点P是三角形的内心,图2所求作的点P是三角形的外心 C、图1所求作的点P是三角形的外心,图2所求作的点P是三角形的内心 D、图1所求作的点P是三角形的外心,图2所求作的点P是三角形的重心5. 某地兴建的幸福小区的三个出口A、B、C的位置如图所示,物业公司计划在不妨碍小区规划的建设下,想在小区内修建一个电动车充电桩,以方便业主,要求到三个出口的距离都相等,则充电桩应该在 ( )
A、图1所求作的点P是三角形的内心,图2所求作的点P是三角形的重心 B、图1所求作的点P是三角形的内心,图2所求作的点P是三角形的外心 C、图1所求作的点P是三角形的外心,图2所求作的点P是三角形的内心 D、图1所求作的点P是三角形的外心,图2所求作的点P是三角形的重心5. 某地兴建的幸福小区的三个出口A、B、C的位置如图所示,物业公司计划在不妨碍小区规划的建设下,想在小区内修建一个电动车充电桩,以方便业主,要求到三个出口的距离都相等,则充电桩应该在 ( )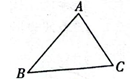 A、三条高线的交点处 B、三条中线的交点处 C、三个角的平分线的交点处 D、三条边的垂直平分线的交点处6. 如图是作△ABC的作图痕迹,则此作图的已知条件是( )
A、三条高线的交点处 B、三条中线的交点处 C、三个角的平分线的交点处 D、三条边的垂直平分线的交点处6. 如图是作△ABC的作图痕迹,则此作图的已知条件是( ) A、已知两边及夹角 B、已知三边 C、已知两角及夹边 D、已知两边及一边对角7. 如图,用三角尺可按下面方法画角平分线:在已知的∠AOB 的两边上分别取点M、N,使OM=ON,再分别过点M、N作OA、OB的垂线,交点为P,画射线OP.可证得△POM≌△PON,OP平分∠AOB.以上依画法证明△POM≌△PON根据的是( )
A、已知两边及夹角 B、已知三边 C、已知两角及夹边 D、已知两边及一边对角7. 如图,用三角尺可按下面方法画角平分线:在已知的∠AOB 的两边上分别取点M、N,使OM=ON,再分别过点M、N作OA、OB的垂线,交点为P,画射线OP.可证得△POM≌△PON,OP平分∠AOB.以上依画法证明△POM≌△PON根据的是( ) A、SSS B、SAS C、AAS D、HL8. 如图,A,B两点在正方形网格的格点上,每个方格都是边长为1的正方形,点C也在格点上,且△ABC为等腰三角形,满足条件的点C有( )
A、SSS B、SAS C、AAS D、HL8. 如图,A,B两点在正方形网格的格点上,每个方格都是边长为1的正方形,点C也在格点上,且△ABC为等腰三角形,满足条件的点C有( ) A、6个 B、7个 C、8个 D、9个9. 如图,在△ABC中,∠BAC=90°,AB≠AC.用无刻度的直尺和圆规在BC边上找一点D,使△ACD为等腰三角形.下列作法错误的是( )A、
A、6个 B、7个 C、8个 D、9个9. 如图,在△ABC中,∠BAC=90°,AB≠AC.用无刻度的直尺和圆规在BC边上找一点D,使△ACD为等腰三角形.下列作法错误的是( )A、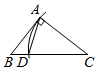 B、
B、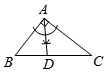 C、
C、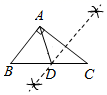 D、
D、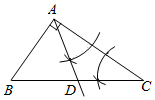 10. 如图,在 的正方形网格中,以 为边画直角 ,使点 在格点上,满足这样条件的点 共( )个.
10. 如图,在 的正方形网格中,以 为边画直角 ,使点 在格点上,满足这样条件的点 共( )个. A、2 B、4 C、6 D、811. 已知线段 , , ,求作: ,使 , , .下面的作图顺序正确的是( )
A、2 B、4 C、6 D、811. 已知线段 , , ,求作: ,使 , , .下面的作图顺序正确的是( )①以点 为圆心,以 为半径画弧,以点 为圆心,以 为半径画弧,两弧交于 点;②作线段 等于 ;③连接 , ,则 就是所求作图形.
A、①②③ B、③②① C、②①③ D、②③①12. 如图,在正方形方格中,各正方形的顶点叫做格点,三个顶点都在格点上的三角形称为格点三角形。图中 是格点三角形,请你找出方格中所有与 全等,且以A为顶点的格点三角形.这样的三角形共有个( 除外). 13. 尺规作图(保留作图痕迹,不要求写出作法):
13. 尺规作图(保留作图痕迹,不要求写出作法):如图,已知线段m,n.求作 , 使.
 14. 如图,已知.
14. 如图,已知. (1)、尺规作出角平分线;(2)、尺规作中线;(3)、作边的高线.15. 如图,在 的网格中, 的三个顶点都在格点上.
(1)、尺规作出角平分线;(2)、尺规作中线;(3)、作边的高线.15. 如图,在 的网格中, 的三个顶点都在格点上.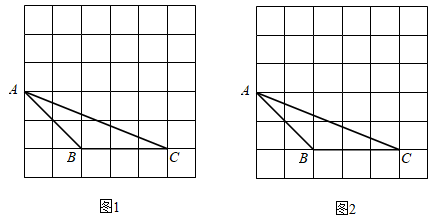 (1)、在图1中画出 ,使 与 全等,顶点D在格点上.(2)、在图2中过点B画出平分 面积的直线l.16. 人教版初中数学教科书八年级上册第35-36页告诉我们作一个三角形与已知三角形全等的方法:
(1)、在图1中画出 ,使 与 全等,顶点D在格点上.(2)、在图2中过点B画出平分 面积的直线l.16. 人教版初中数学教科书八年级上册第35-36页告诉我们作一个三角形与已知三角形全等的方法:已知: .
求作: ,使得 ≌ .
作法:如图.
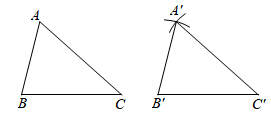
( 1 )画 ;
( 2 )分别以点 , 为圆心,线段 , 长为半径画弧,两弧相交于点 ;
( 3 )连接线段 , ,则 即为所求作的三角形.
请你根据以上材料完成下列问题:
(1)、完成下面证明过程(将正确答案填在相应的横线上):证明:由作图可知,在 和 中,
∴ ≌_▲_.
(2)、这种作一个三角形与已知三角形全等的方法的依据是.(填序号)①AAS;②ASA;③SAS;④SSS
17. 在如图所示的6×6的网格中,每个小正方形的边长均为1个单位.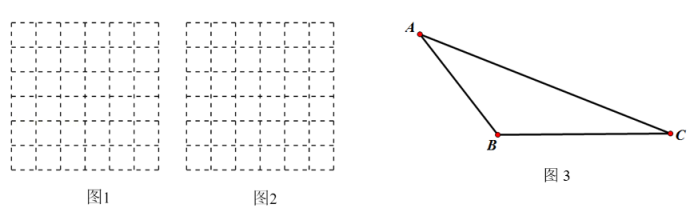 (1)、请你在图1中画一个以格点为顶点,面积为6个平方单位的等腰三角形:(2)、请你在图2中画一个以格点为顶点,一条直角边边长为的直角三角形.(3)、请你在图3中画出△ABC的边BC上的高AD,∠ACB的角平线CE18. 如图,在边长为1的小正方形所组成的网格上,每个小正方形的顶点都称为“格点”, 的顶点都在格点上.
(1)、请你在图1中画一个以格点为顶点,面积为6个平方单位的等腰三角形:(2)、请你在图2中画一个以格点为顶点,一条直角边边长为的直角三角形.(3)、请你在图3中画出△ABC的边BC上的高AD,∠ACB的角平线CE18. 如图,在边长为1的小正方形所组成的网格上,每个小正方形的顶点都称为“格点”, 的顶点都在格点上.
⑴直接判断的形状.
⑵画出关于直线的对称图形△ .
⑶在直线上作一点 , 使得最小,
二、作图-角平分线
-
19. 如图,∠AOB=40°,以点O为圆心,适当长为半径画弧,交OA,OB于C,D两点,分别以C,D为圆心,大于CD的长为半径画弧,两弧在∠AOB的内部相交于点E,画射线OE,过点E作OB的平行线交OA于点F,则∠OEF的度数为( )
 A、20° B、30° C、40° D、140°20. 下列尺规作图分别表示:①作一个角的平分线,②作一条线段的垂直平分线.其中作法正确的是( )
A、20° B、30° C、40° D、140°20. 下列尺规作图分别表示:①作一个角的平分线,②作一条线段的垂直平分线.其中作法正确的是( )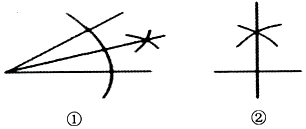 A、① B、② C、①② D、无21. 如图,在△ABC中,∠C=90°,AC>BC.用直尺和圆规在边AC上确定一点P,使点P到AB、BC的距离相等,则符合要求的作图痕迹( )A、
A、① B、② C、①② D、无21. 如图,在△ABC中,∠C=90°,AC>BC.用直尺和圆规在边AC上确定一点P,使点P到AB、BC的距离相等,则符合要求的作图痕迹( )A、 B、
B、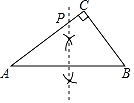 C、
C、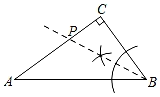 D、
D、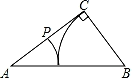 22. 用尺规作一个角的角平分线,下列作法中错误的是( )A、
22. 用尺规作一个角的角平分线,下列作法中错误的是( )A、 B、
B、 C、
C、 D、
D、 23. 如图,在中, , 以点B为圆心,适当长为半径画弧,交于点M,交于点N,分别以点M、N为圆心,大于的长为半径画弧,两弧在的内部相交于点P,画射线 , 交于点D,若 , 则的度数是( )
23. 如图,在中, , 以点B为圆心,适当长为半径画弧,交于点M,交于点N,分别以点M、N为圆心,大于的长为半径画弧,两弧在的内部相交于点P,画射线 , 交于点D,若 , 则的度数是( )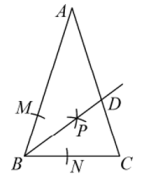 A、 B、 C、 D、24. 如图,是平行四边形的对角线,平分 , 交于点.
A、 B、 C、 D、24. 如图,是平行四边形的对角线,平分 , 交于点. (1)、请用尺规作的角平分线 , 交于点(要求保留作图痕迹,不写作法,在确认答案后,请用黑色笔将作图痕迹再填涂一次):(2)、根据图形猜想四边形为平行四边形,请将下面的证明过程补充完整.
(1)、请用尺规作的角平分线 , 交于点(要求保留作图痕迹,不写作法,在确认答案后,请用黑色笔将作图痕迹再填涂一次):(2)、根据图形猜想四边形为平行四边形,请将下面的证明过程补充完整.证明:∵四边形是平行四边形,
∴
∵ ▲ .(两线平行,内错角相等).
又∵平分 , 平分 ,
∴ ,
∴.
∴ ▲ ( )(填推理的依据)
又∵四边形是平行四边形.
∴.
∴四边形为平行四边形( )(填推理的依据),
25. 如图,在△ABC中,AB=AC,BD是△ABC的角平分线.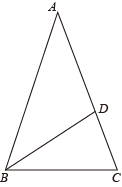 (1)、作∠ACB的角平分线,交AB于点E(尺规作图,不写作法,保留作图痕迹);(2)、求证:AD=AE.26. 如图是的正方形网格,请仅用无刻度的直尺按要求完成以下作图(保留作图痕迹).
(1)、作∠ACB的角平分线,交AB于点E(尺规作图,不写作法,保留作图痕迹);(2)、求证:AD=AE.26. 如图是的正方形网格,请仅用无刻度的直尺按要求完成以下作图(保留作图痕迹).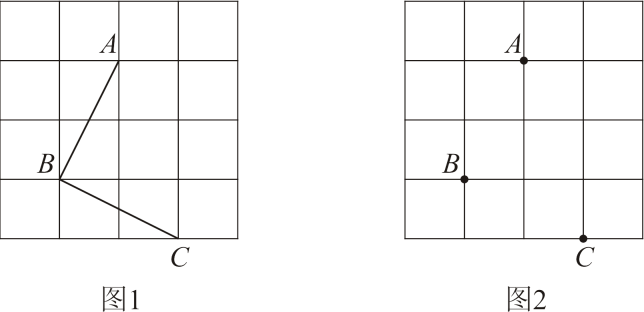 (1)、在图1中作的角平分线;(2)、在图2中过点C作一条直线l,使点A,B到直线l的距离相等.27. 【问题提出】如何用圆规和无刻度的直尺作一条直线或圆弧平分已知扇形的面积?
(1)、在图1中作的角平分线;(2)、在图2中过点C作一条直线l,使点A,B到直线l的距离相等.27. 【问题提出】如何用圆规和无刻度的直尺作一条直线或圆弧平分已知扇形的面积?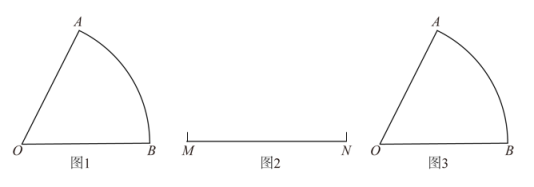
【初步尝试】如图1,已知扇形 , 请你用圆规和无刻度的直尺过圆心作一条直线,使扇形的面积被这条直线平分;
【问题联想】如图2,已知线段 , 请你用圆规和无刻度的直尺作一个以为斜边的等腰直角三角形;
【问题再解】如图3,已知扇形 , 请你用圆规和无刻度的直尺作一条以点为圆心的圆弧,使扇形的面积被这条圆弧平分.
(友情提醒:以上作图均不写作法,但需保留作图痕迹)
28. 两个村庄M,N与两条公路AC,AB的位置如图所示,现打算在O处建一个垃圾回收站,要求回收站到两个村庄M,N的距离必须相等,到两条公路AC,AB的距离也必须相等,那么点O应选在何处?请在图中用尺规作图中找出点O.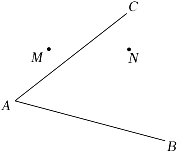 29. 如图,已知△ABC,请利用尺规作图法在AC上求作一点P,使得BP平分∠ABC.(保留作图痕迹,不写作法)
29. 如图,已知△ABC,请利用尺规作图法在AC上求作一点P,使得BP平分∠ABC.(保留作图痕迹,不写作法)
三、作图-垂直平分线
-
30. 如图,小明在学了尺规作图后,作了一个图形,其作图步骤是:①作线段AB=2,分别以点A、B为圆心,以AB长为半径画弧,两弧相交于点C、D;②连接AC、BC,作直线CD,且CD与AB相交于点H.则下列说法正确的是( )
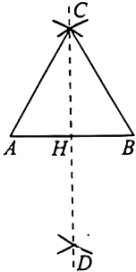 A、△ABC是等边三角形 B、AB⊥CD C、AH=BH D、∠ACD=45°31. 如图,在Rt△ABC中,观察作图痕迹,若BF=2,则CF的长为( )
A、△ABC是等边三角形 B、AB⊥CD C、AH=BH D、∠ACD=45°31. 如图,在Rt△ABC中,观察作图痕迹,若BF=2,则CF的长为( ) A、 B、3 C、2 D、32. 已知△ABC(AB<AC<BC),用尺规作图的方法在BC上取一点P,使PA+PC=BC,下列选项正确的是( )A、
A、 B、3 C、2 D、32. 已知△ABC(AB<AC<BC),用尺规作图的方法在BC上取一点P,使PA+PC=BC,下列选项正确的是( )A、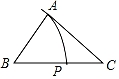 B、
B、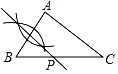 C、
C、 D、
D、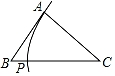 33. 如图,已知线段AB=4,利用尺规作AB的垂直平分线,步骤如下:①分别以点A和点B为圆心,以一定长度m为半径作弧,两弧相交于点C和点D;②作直线CD,直线CD就是线段AB的垂直平分线.下列各数中,m的值可能是( )
33. 如图,已知线段AB=4,利用尺规作AB的垂直平分线,步骤如下:①分别以点A和点B为圆心,以一定长度m为半径作弧,两弧相交于点C和点D;②作直线CD,直线CD就是线段AB的垂直平分线.下列各数中,m的值可能是( ) A、1 B、1.5 C、2 D、2.534. 如图,在中, , , 是边上的中线.按下列步骤作图:①分别以点和点为圆心,大于的长为半径作弧,两弧相交于点 , ;②作直线 , 分别交 , 于点 , ;③连接 , . 则下列结论错误的是( )
A、1 B、1.5 C、2 D、2.534. 如图,在中, , , 是边上的中线.按下列步骤作图:①分别以点和点为圆心,大于的长为半径作弧,两弧相交于点 , ;②作直线 , 分别交 , 于点 , ;③连接 , . 则下列结论错误的是( ) A、 B、 C、 D、35. 如图,已知中, , , .
A、 B、 C、 D、35. 如图,已知中, , , .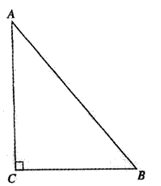 (1)、作的垂直平分线,分别交、于点、;(要求:尺规作图,不写作法,保留作图痕迹)(2)、在(1)的条件下,连接CD,求的周长.36. 如图,已知线段和线段.
(1)、作的垂直平分线,分别交、于点、;(要求:尺规作图,不写作法,保留作图痕迹)(2)、在(1)的条件下,连接CD,求的周长.36. 如图,已知线段和线段. (1)、用直尺和圆规按下列要求作图.(请保留作图痕迹,并标明相应的字母,不写作法)
(1)、用直尺和圆规按下列要求作图.(请保留作图痕迹,并标明相应的字母,不写作法)①作线段的垂直平分线 , 交线段于点;
②以线段为对角线,作矩形 , 使得 , 并且点在线段的上方.
(2)、当 , 时,求(1)中所作矩形的面积.37. 如图①、图②是6X6的正方形网格,每个小正方形的边长均为1,每个小正方形的顶点称为格点,△ABC的顶点均在格点上.只用无刻度的直尺,在给定的网格中,分别按下列要求画图,保留适当的作图痕迹. (1)、在图①中的线段AB上找一点D,连结CD,使∠BCD=∠BDC.(2)、在图②中的线段AC上找一点E,连结BE,使∠ABE=∠BAE.38. 图①、图②均是6×6的正方形网格,每个小正方形的边长均为1,每个小正方形的顶点称为格点,点A、B、C均在格点上,只用无刻度的直尺,分别在给定的网格中找一格点P,按下列要求作图.
(1)、在图①中的线段AB上找一点D,连结CD,使∠BCD=∠BDC.(2)、在图②中的线段AC上找一点E,连结BE,使∠ABE=∠BAE.38. 图①、图②均是6×6的正方形网格,每个小正方形的边长均为1,每个小正方形的顶点称为格点,点A、B、C均在格点上,只用无刻度的直尺,分别在给定的网格中找一格点P,按下列要求作图. (1)、在图①中,连结PA、PB,使PA=PB.(2)、在图2中,连结PA、PB、PC,使PA=PB=PC.39. 如图,在矩形ABCD中,AC是对角线.
(1)、在图①中,连结PA、PB,使PA=PB.(2)、在图2中,连结PA、PB、PC,使PA=PB=PC.39. 如图,在矩形ABCD中,AC是对角线.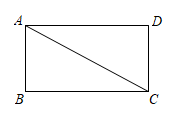 (1)、实践与操作:利用尺规作线段AC的垂直平分线,垂足为点O,交边AD于点E,交边BC于点F(要求:尺规作图并保留作图痕迹,不写作法,标明字母),(2)、猜想与证明:试猜想线段AE与CF的数量关系,并加以证明.40. 如图
(1)、实践与操作:利用尺规作线段AC的垂直平分线,垂足为点O,交边AD于点E,交边BC于点F(要求:尺规作图并保留作图痕迹,不写作法,标明字母),(2)、猜想与证明:试猜想线段AE与CF的数量关系,并加以证明.40. 如图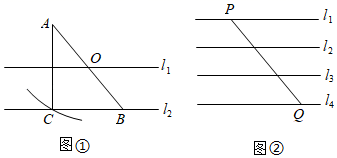 (1)、如图①,O为AB的中点,直线l1、l2分别经过点O、B,且l1∥l2 , 以点O为圆心,OA长为半径画弧交直线l2于点C,连接AC.求证:直线l1垂直平分AC;(2)、如图②,平面内直线l1∥l2∥l3∥l4 , 且相邻两直线间距离相等,点P、Q分别在直线l1、l4上,连接PQ.用圆规和无刻度的直尺在直线l4上求作一点D,使线段PD最短.(两种工具分别只限使用一次,并保留作图痕迹)41. 综合与实践
(1)、如图①,O为AB的中点,直线l1、l2分别经过点O、B,且l1∥l2 , 以点O为圆心,OA长为半径画弧交直线l2于点C,连接AC.求证:直线l1垂直平分AC;(2)、如图②,平面内直线l1∥l2∥l3∥l4 , 且相邻两直线间距离相等,点P、Q分别在直线l1、l4上,连接PQ.用圆规和无刻度的直尺在直线l4上求作一点D,使线段PD最短.(两种工具分别只限使用一次,并保留作图痕迹)41. 综合与实践问题情境:我国东周到汉代一些出土实物上反映出一些几何作图方法,如侯马铸铜遗址出土车軎范、芯组成的(如图1),它的端面是圆形,如图2是用“矩”(带直角的角尺)确定端面圆心的方法:将“矩”的直角尖端A沿圆周移动,直到 ,在圆上标记A,B,C三点;将“矩”向右旋转,使它左侧边落在A,B点上,“矩”的另一条边与圆的交点标记为D点,这样就用“矩”确定了圆上等距离的A,B,C,D四点,连接AD,BC相交于点O,即O为圆心.
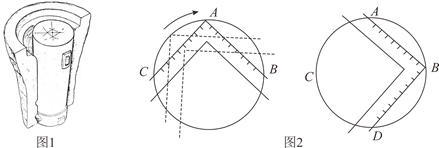
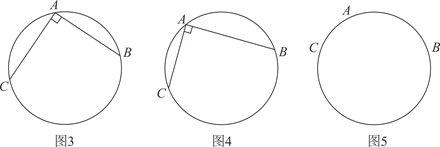 (1)、问题解决:请你根据“问题情境”中提供的方法,用三角板还原我国古代几何作图确定圆心O.如图3,点A,B,C在 上, ,且 ,请作出圆心O.(保留作图痕迹,不写作法)(2)、类比迁移:小梅受此问题的启发,在研究了用“矩”(带直角的角尺)确定端面圆心的方法后发现,如果AB和AC不相等,用三角板也可以确定圆心O.如图4,点A,B,C在 上, ,请作出圆心O.(保留作图痕迹,不写作法)(3)、拓展探究:小梅进一步研究,发现古代由“矩”度量确定圆上等距离点时存在误差,用平时学的尺规作图的方法确定圆心可以减少误差.如图5,点A,B,C是 上任意三点,请用不带刻度的直尺和圆规作出圆心O.(保留作图痕迹,不写作法)请写出你确定圆心的理由: ▲ .
(1)、问题解决:请你根据“问题情境”中提供的方法,用三角板还原我国古代几何作图确定圆心O.如图3,点A,B,C在 上, ,且 ,请作出圆心O.(保留作图痕迹,不写作法)(2)、类比迁移:小梅受此问题的启发,在研究了用“矩”(带直角的角尺)确定端面圆心的方法后发现,如果AB和AC不相等,用三角板也可以确定圆心O.如图4,点A,B,C在 上, ,请作出圆心O.(保留作图痕迹,不写作法)(3)、拓展探究:小梅进一步研究,发现古代由“矩”度量确定圆上等距离点时存在误差,用平时学的尺规作图的方法确定圆心可以减少误差.如图5,点A,B,C是 上任意三点,请用不带刻度的直尺和圆规作出圆心O.(保留作图痕迹,不写作法)请写出你确定圆心的理由: ▲ .