浙教版备考2023年中考数学一轮复习46.线段、射线、直线、角

试卷更新日期：2022-12-31 类型：一轮复习

进入出卷网下载

一、单选题（每题3分，共30分）

1. 如图，工人砌墙时，先在两个墙脚的位置分别插一根木桩，再拉一条直的参照线，就能使砌的砖在一条直线上.这样做应用的数学知识是（）

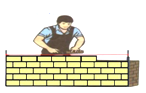A、两点之间，线段最短 B、两点确定一条直线 C、垂线段最短 D、三角形两边之和大于第三边

查看试题解析
2. 如图，从学校A到书店B有①、②、③、④四条路线，其中最短的路线是（）

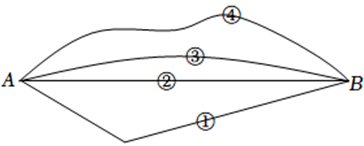A、① B、② C、③ D、④

查看试题解析
3. 如图，利用工具测量角，则 $∠ 1$ 的大小为（）

A、30° B、60° C、120° D、150°

查看试题解析
4. 如图，某海域中有A，B，C三个小岛，其中A在B的南偏西40°方向，C在B的南偏东35°方向，且B，C到A的距离相等，则小岛C相对于小岛A的方向是（）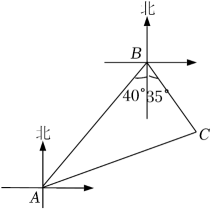

A、北偏东70° B、北偏东75° C、南偏西70° D、南偏西20°

查看试题解析
5. 互不重合的A、B、C三点在同一直线上，已知AC＝2a+1，BC＝a+4，AB＝3a，这三点的位置关系是（）

A、点A在B、C两点之间 B、点B在A、C两点之间 C、点C在A、B两点之间 D、无法确定

查看试题解析
6. 棋盘上有黑、白两色棋子若干，如果两颗棋子连成的直线上只有颜色相同的棋子，我们就称“同棋共线”．右图中“同棋共线”的直线共有（）

A、8条 B、10条 C、12条 D、16条

查看试题解析
7. 数轴上到表示数3的点距离5个单位的点所表示的数为（）

A、2 B、2或8 C、8 D、-2或8

查看试题解析
8. 如图，已知A，B（B在A的左侧）是数轴上的两点，点A对应的数为4，且 $A B = 6$ ，动点P从点A出发，以每秒2个单位长度的速度沿数轴向左运动，在点P的运动过程中，M，N始终为AP，BP的中点，设运动时间为 $t (t > 0)$ 秒，则下列结论中正确的有（）
①B对应的数是2；②点P到达点B时， $t = 3$ ；③ $B P = 2$ 时， $t = 2$ ；④在点P的运动过程中，线段MN的长度不变．

A、①③④ B、②③④ C、②③ D、②④

查看试题解析
9. 如图1，当光线从空气斜入射到某种透明的液体时发生了折射，满足入射角∠1与折射角∠2的度数比为3∶2．如图2，在同一平面上，两条光线同时从空气斜射入这种液体中，两条入射光线与水平液面夹角分别为α，β，在液体中两条折射光线的夹角为γ，则α，β，γ三者之间的数量关系为（）

A、 $\frac{2}{3}$ （α＋β）＝γ B、 $\frac{2}{3}$ （α＋β）＝120°－γ C、α＋β＝γ D、α＋β＋γ＝180°

查看试题解析
10. 如图，C、D是线段AB上两点，M、N分别是线段AD，BC的中点，下列结论：
①若AD＝BM，则AB＝3BD；②AC＝BD，则AM＝BN；③AC﹣BD＝2（MC﹣DN）；④2MN＝AB﹣CD．

其中正确的结论是（）

A、①②③ B、③④ C、①②④ D、①②③④

查看试题解析

二、填空题（每题4分，共24分）

11. 度分秒转换：32.6°=°′；

查看试题解析
12. 如图，以点О为端点的射线有条.

查看试题解析
13. 如图摆放一副三角板，直角顶点重合，直角边所在直线分别重合，那么∠BAC的大小为

查看试题解析
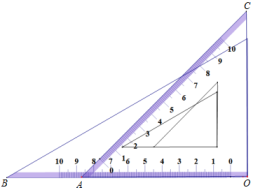14. 如图，PA，PB表示以P为起点的两条公路，其中公路PA的走向是南偏西34 $°$ ，公路PB的走向是南偏东56 $°$ ，则这两条公路的夹角∠APB＝°．

查看试题解析
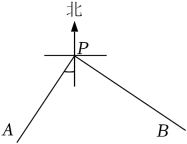15. 已知∠α=60°，则∠α的余角等于度．

查看试题解析
16. 七巧板是我们祖先的一项卓越创造，被西方人誉为“东方魔板” $.$ 小林将图1的一副七巧板拼成图2的“衣服” $($ 阴影部分 $)$ ，并将它放入方格图中，方格图中的小正方形边长为1，则这件“衣服”的周长为 $(\sqrt{2}$ 取1.4）.

查看试题解析

三、作图题（共4题，共30分）

17. 如图，平面上有A，B，C，D四个点，根据下列语句作图：

⑴画直线AC.

⑵线段AD与线段BC相交于点O.

⑶射线AB与射线CD相交于点P.

查看试题解析
18. 已知： $∠ α$ 和线段a．求作： $△ A B C$ ，使 $A B = 2 a$ ， $B C = 3 a$ ， $∠ A B C = ∠ α$ ．（不要求写作法）

查看试题解析
19. 已知点直线BC及直线外一点A（如图），按要求完成下列问题：

(1)、画出射线CA，线段AB．过C点画CD⊥AB，垂足为点D；

(2)、比较线段CD和线段CA的大小，并说明理由；

(3)、在以上的图中，互余的角为，互补的角为．（各写出一对即可）

查看试题解析
20. 如图所示，一艘客轮沿东北方向 $OC$ 行驶，在海上 $O$ 处发现灯塔 $A$ 在北偏西 $30^{\circ}$ 方向上，灯塔 $B$ 在南偏东 $60^{\circ}$ 方向上.

(1)、在图中画出射线 $OA$ ， $OB$ ， $OC$ .

(2)、求 $∠ AOC$ 与 $∠ BOC$ 的度数，你发现了什么?

查看试题解析

四、解答题（共4题，共36分）

21. 如图，∠AOE＝80°，OB平分∠AOC，OD平分∠COE，∠AOB＝15°.

(1)、求∠COD度数；

(2)、若OA表示时钟时针，OD表示分针，且OA指在3点过一点，求此时的时刻是多少？

查看试题解析
22. 如图，已知线段AB上有两点C、D，且AC：CD：DB＝2：3：4，E，F分别为AC、DB的中点，EF＝12cm.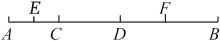

(1)、线段BC的长；

(2)、线段AB的长；

(3)、若点G在直线AB上，且GB＝3cm，求线段DG的长.

查看试题解析
23. 已知在数轴上点M、N表示的数分别为a，b，点M、N两点之间的距离表示为 $| a - b |$ 或 $| b - a |$ ，记为 $| M N | = | a - b | = | b - a |$ ．如图，已知数轴上点A表示的数为6，B是数轴上在A左侧的一点，且A，B两点间的距离为10．点P是数轴上任意一点，

(1)、数轴上点B表示的数是；

(2)、如果点P到点A、点B的距离相等，那么点P表示的数是；

(3)、若点P到点A、点B的距离之和等于14，则点P表示的数为；

(4)、若点P从点A出发，以每秒6个单位长度的速度沿数轴向左匀速运动．动点Q从点B出发，以每秒4个单位长度的速度沿数轴向左匀速运动，若点P、Q同时出发，运动时间为t．求：
①当 $t = 1$ 秒时P，Q两点间的距离为 ▲ ；

②当点P运动多少秒时，点P与点Q相遇？

③当点P与点Q间的距离为8个单位长度时t的值为 ▲ ．

查看试题解析
24. 【方法感悟】阅读下面材料：
点A，B在数轴上分别表示实数a，b，A，B两点之间的距离表示为 $| A B |$ .如图1，从数轴上看，若点A，B表示的分别是1，4则 $| A B | = | 4 - 1 | = 3$ 或 $| A B | = | 1 - 4 | = 3$ ；

若点A，B表示的数分别是 $- 1$ ， 4则 $| A B | = | 4 - (- 1) | = 4 + 1 = 5$ 或 $| A B | = | - 1 - 4 | = | - 5 | = 5$ ；

若点A，B表示的数分别是 $- 1$ ， $- 4$ ，则 $| A B | = | (- 1) - (- 4) | = | - 1 + 4 | = 3$ 或 $| A B | = | - 4 - (- 1) | = | - 4 + 1 | = 3$ ．

【归纳】若点A，B表示的数分别是 $x_{1}$ ， $x_{2}$ 则 $| A B | = | x_{1} - x_{2} |$ 或 $| A B | = | x_{2} - x_{1} |$ ．

【知识迁移】

(1)、如图1，点A，B表示的数分别是 $- 4.5$ ， b且 $| A B | = 3$ ，则 $b =$ ；

(2)、如图2，点A，B表示的数分别是 $x_{1}$ ， $x_{2}$ ，若把 $A B$ 向左平移 $| A B |$ 个单位，则点A与 $- 50$ 重合，若把 $A B$ 向右平移 $| A B |$ 个单位，则点B与70重合，那么 $x_{1} =$ ， $x_{2} =$ ；

(3)、【拓展应用】
一天，美羊羊去问村长爷爷的年龄，村长爷爷说：“我若是你现在这么大，你还要40年才出生呢，你若是我现在这么大，我已经是老寿星了，116岁了，哈哈！”美羊羊纳闷，请问村长爷爷现在到底是多少岁？美羊羊现在又是几岁？请写出解题思路.

(4)、结合几何意义，求 $| x - 1 | + | x - 2 | + | x - 3 | + | x - 4 | + | x - 5 |$ 最小值.

查看试题解析

浙教版备考2023年中考数学一轮复习46.线段、 射线、 直线、角

一、单选题（每题3分，共30分）

二、填空题（每题4分，共24分）

三、作图题（共4题，共30分）

四、解答题（共4题，共36分）

浙教版备考2023年中考数学一轮复习46.线段、射线、直线、角