2022-2023学年苏科版九年级上学期数学期末模拟试卷2

试卷更新日期：2022-12-31 类型：期末考试

进入出卷网下载

一、单选题（每题2分，共12分）

1. 一元二次方程 $x (x - 3) = 3 - x$ 的根是（）

A、-1 B、1和3 C、-1和3 D、3

查看试题解析
2. 若关于 $x$ 的二次函数 $y = x^{2} - 3 x + m$ 的图象与 $x$ 轴有两个交点，且 $m \geq - 3$ ，则从满足条件的所有整数 $m$ 中随机选取一个，恰好是负数的概率是（）

A、 $\frac{1}{3}$ B、 $\frac{1}{2}$ C、 $\frac{2}{3}$ D、 $\frac{5}{6}$

查看试题解析
3. 为了从甲、乙两名同学中选出一名同学代表班级参加学校的投篮比赛，对甲、乙两人进行了5次投篮试投比赛，试投每人每次投球10个，两人5次试投的成绩统计图如图所示．以下说法错误的是（）

A、甲同学5次试投进球个数的众数是8 B、甲、乙两名同学投篮成绩甲较稳定 C、甲、乙同学5次试投进球个数的平均数相同 D、乙同学5次试投进球个数的中位数是8

查看试题解析
4. 如图，△ABC中，E是AB的中点，过点E作ED∥BC，交AC于点D，则△AED与四边形BCDE的面积比是（）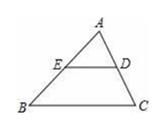

A、1：1 B、1：2 C、1：3 D、1：4

查看试题解析
5. 如图，在Rt△ABC中，∠ACB＝90°，CB＝7，AC＝9，以C为圆心、3为半径作⊙C，P为⊙C上一动点，连接AP、BP，则 $\frac{1}{3}$ AP+BP的最小值为（）

A、3 $\sqrt{2}$ . B、4 $\sqrt{3}$ C、3 $\sqrt{5}$ D、5 $\sqrt{2}$

查看试题解析
6. 已知二次函数 $y = a x^{2} + b x + c$ （ $a \neq 0$ ）图象的对称轴为直线 $x = - 1$ ，部分图象如图所示，下列结论中：① $a b c > 0$ ；② $b^{2} - 4 a c > 0$ ；③ $4 a + c > 0$ ；④若 $t$ 为任意实数，则有 $a - b t \leq a t^{2} + b$ ；⑤当图象经过点 $(\frac{1}{2} ， 2)$ 时，方程 $a x^{2} + b x + c - 2 = 0$ 的两根为 $x_{1}$ ， $x_{2}$ $(x_{1} < x_{2})$ ，则 $x_{1} + 2 x_{2} = - \frac{3}{2}$ ，其中正确的结论有（）

A、①②③ B、②③⑤ C、②③④⑤ D、②③④

查看试题解析

二、填空题（每题2分，共20分）

7. 若 $\frac{a}{3} = \frac{b}{2}$ ≠0，则 $\frac{3 a - 2 b}{a + b}$ =.

查看试题解析
8. 平移抛物线y=2x² ，使其顶点为（2，3），平移后的抛物线是

查看试题解析
9. 若一元二次方程 $x^{2} - (2 m + 3) x + m^{2} = 0$ 有两个不相等的实数根 $x_{1}$ ， $x_{2}$ ，且 $x_{1} + x_{2} = x_{1} x_{2}$ ，则 $m$ 的值是．

查看试题解析
10. 如图，点D是△ABC边BC上的一点，且 $\frac{B D}{D C} = \frac{3}{4}$ ，点E是AD的中点，连接BE并延长交AC于点F，则 $\frac{A F}{F C}$ 的值为.

查看试题解析
11. 如图， $△ A B C$ 内接于 $⊙ O$ ， $∠ B A C = 60 °$ ， D是 $B C$ 的中点，且 $∠ A O D = 166 °$ ， $A E ， C F$ 分别是 $B C ， A B$ 边上的高，则 $∠ B C F$ 的大小 $=$ 度.

查看试题解析
12. 如图，如果AB、AC分别是圆O的内接正三角形和内接正方形的一条边，BC一定是圆O的内接正n边形的一条边，那么n= ．

查看试题解析
13. 如图，身高1.8米的轩轩从一盏路灯下的B处向前走了4米到达点C处时，发现自己在地面上的影子CE长与他的身高一样，则路灯的高AB为米.

查看试题解析
14. 如图，在平行四边形 $A B C D$ 中，点E是边BC上的黄金分割点，且 $B E > C E$ ， AE与BD相交于点 $F$ .那么 $F D ： B F$ 的值为.

查看试题解析
15. 如图所示，在矩形 $ABCD$ 中， $AD = 6$ ， $AB = 12$ ， $N$ 是边 $AB$ 上的一个动点，将 $△ AND$ 沿 $DN$ 折叠得 $△ DMN .$ 分别连接 $BM$ 、 $CM$ ，若 $△ BMC$ 为等腰三角形，则 $AN$ 的长为．

查看试题解析
16. 将抛物线y＝﹣x²﹣4x（﹣4≤x≤0）沿y轴折叠后得另一条抛物线，若直线y＝x+b与这两条抛物线共有3个公共点，则b的取值范围为.

查看试题解析

三、解答题（共11题，共88分）

17. 解方程： $2 x^{2} - x = 6$

查看试题解析
18. 体育课上，王老师安排李明、王强、张三、田武四个同学练习传球，每个同学拿到球后随机传给下一个同学．

(1)、若李明第一个拿到球，他将球传给王强的概率为．

(2)、若从李明开始传球，则经过两次传球后，球回到李明手上的概率为多少？

查看试题解析
19. 某超市销售一种成本为每台20元的台灯，规定销售单价不低于成本价，又不高于每台32元．销售中平均每月销售量y（台）与销售单价x（元）的关系可以近似地看做一次函数，如下表所示：
x
22
24
26
28
y
90
80
70
60

(1)、请求出y与x之间的函数关系式；

(2)、设超市每月台灯销售利润为 $ω$ （元），求 $ω$ 与x之间的函数关系式，当x取何值时， $ω$ 的值最大？最大值是多少？

查看试题解析
20. 某中学八年级甲、乙两班分别选5名同学参加“防疫宣传”演讲比赛，其预赛成绩 $($ 单位：分 $)$ 如图所示：
根据以上信息，解答下列问题：

(1)、求出表中的 $a$ 、 $b$ 、 $c$ 、 $d$ ；

平均数
中位数
众数
方差
甲班
8.5
$b$
8.5
$d$
乙班
$a$
8
$c$
1.6

(2)、请你任选一组统计量描述两个班的成绩水平？

(3)、乙班小明说：“我的成绩在我们班是中等水平”，你知道他是几号选手吗？

查看试题解析
21. 如图，在△ABC中，AC＝4.

(1)、在AC上求作一点D，连接BD，使得△ABD∽△ACB；（要求：尺规作图，不写作法，保留作图痕迹）

(2)、点M，N分别是BD、BC中点，若AD＝1，求 $\frac{A M}{A N}$ 的值.

查看试题解析
22. 如图，AB是⊙O的直径，点C在AB的延长线上，AD平分∠CAE交⊙O于点D，且AE⊥CD，垂足为点E．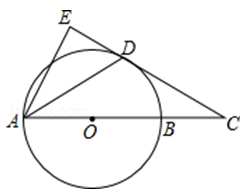

(1)、求证：直线CE是⊙O的切线．

(2)、若BC=3，CD=3 $\sqrt{2}$ ，求半径OB与线段AE的长．

查看试题解析
23. 如图，四边形ABCD是矩形，对角线相交于点O，点E为线段AO上一点（不含端点），点F是点E关于AD的对称点，连接CF与BD相交于点G.

(1)、证明：AF $/ /$ BD；

(2)、若 $O G = 1$ ， $O E = 2$ .求BD的长.

查看试题解析
24. 如图，AB是⊙O的直径，D、E为⊙O上位于AB异侧的两点，连接BD并延长至点C，使得CD＝BD，连接AC交00于点F，连接AE、DE、DF.

(1)、证明：∠E＝∠C；

(2)、若∠E＝55°，求∠BDF的度数；

(3)、设DE交AB于点G，若AB＝10，E是 $\overset{⌢}{AEB}$ 的中点，求EG●ED的值

查看试题解析
25. 如图，已知二次函数y=ax²+2x+c的图象经过点C（0，3），与x轴分别交于点A，点B（3，0）。点P是直线BC上方的抛物线上一动点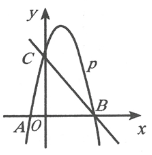

(1)、求二次函数y=ax²+2x+c的表达式；

(2)、连接PO，PC，并把△POC沿y轴翻折，得到四边形POPC.若四边形POP'C为菱形，请求出此时点P的坐标；

(3)、当点P运动到什么位置时，四边形ACPB的面积最大？求出此时P点的坐标和四边形ACPB的最大面积.

查看试题解析
26. 新定义：如果函数G的图象与直线l相交于点A（x₁ ， y₁）和点B（x₂ ， y₂），那么我们把|x₁−x₂|叫做函数G在直线l上的“截距”.

(1)、求双曲线G： $y = \frac{4}{x}$ 与直线l： $y = - 2 x + 6$ 上的“截距”；

(2)、若抛物线 $y = 2 x^{2} + (2 - b) x$ 与直线 $y = - x + b$ 相交于点A（x₁ ， y₁）和点B（x₂ ， y₂），若“截距”为 $\sqrt{6}$ ，且x₁＜x₂＜0，求b的值；

(3)、设m，n为正整数，且 $m \neq 2$ ，抛物线 $y = x^{2} + (3 - m t) x - 3 m t$ 在x轴上的“截距”为d₁ ，抛物线 $y = - x^{2} + (2 t - n) x + 2 n t$ 在x轴上的“截距”为d₂.如果 $d_{1} \geq d_{2}$ 对一切实数t恒成立，求m，n的值.

查看试题解析
27. 如图1， $C$ ， $D$ 是半圆 $A C B$ 上的两点，若直径 $A B$ 上存在一点 $P$ ，满足 $∠ A P C = ∠ B P D$ ，则称 $∠ C P D$ 是 $\overset{⌢}{C D}$ 的“幸运角”.

(1)、如图2， $A B$ 是 $⊙ O$ 的直径，弦 $C E ⊥ A B$ ， $D$ 是 $B C$ 上一点，连结 $E D$ 交 $A B$ 于点 $P$ ，连结 $C P$ ， $∠ C P D$ 是 $\overset{⌢}{C D}$ 的“幸运角”吗？请说明理由；

(2)、设 $\overset{⌢}{C D}$ 的度数为 $n$ ，请用含 $n$ 的式子表示 $\overset{⌢}{C D}$ 的“幸运角”度数；

(3)、在（1）的条件下，直径 $A B = 10$ ， $\overset{⌢}{C D}$ 的“幸运角”为 $90 °$ .
①如图3，连结 $C D$ ，求弦 $C D$ 的长；
②当 $D E = 7 \sqrt{2}$ 时，求 $C E$ 的长.

查看试题解析

	平均数	中位数	众数	方差
甲班	8.5	$b$	8.5	$d$
乙班	$a$	8	$c$	1.6