浙教版备考2023年中考数学一轮复习45.立体图形
试卷更新日期:2022-12-31 类型:一轮复习
一、单选题
-
1. 如图,将矩形绕着它的一边所在的直线1旋转一周,可以得到的立体图形是( )
 A、
A、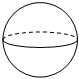 B、
B、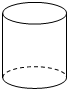 C、
C、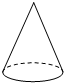 D、
D、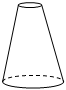 2. ①~④是由相同的小正方体粘在一起的几何体,若组合其中的两个,恰是由6个小正方体构成的长方体,则应选择()
2. ①~④是由相同的小正方体粘在一起的几何体,若组合其中的两个,恰是由6个小正方体构成的长方体,则应选择() A、①③ B、②③ C、③④ D、①④3. 在Rt△ABC中,∠C=90°,AC=3,BC=4,以AC所在直线为轴,把△ABC旋转1周,得到圆锥,则该圆锥的侧面积为( )A、12π B、15π C、20π D、24π4. 如图是一个几何体的三视图,则该几何体的体积为( )
A、①③ B、②③ C、③④ D、①④3. 在Rt△ABC中,∠C=90°,AC=3,BC=4,以AC所在直线为轴,把△ABC旋转1周,得到圆锥,则该圆锥的侧面积为( )A、12π B、15π C、20π D、24π4. 如图是一个几何体的三视图,则该几何体的体积为( ) A、1 B、2 C、 D、45. 如图,锚标浮筒是打捞作业中用来标记锚或沉船位置的,它的上下两部分是圆锥,中间是圆柱(单位:mm).电镀时,如果每平方米用锌0.1千克,电镀1000个这样的锚标浮筒,需要多少千克锌?(π的值取3.14)( )
A、1 B、2 C、 D、45. 如图,锚标浮筒是打捞作业中用来标记锚或沉船位置的,它的上下两部分是圆锥,中间是圆柱(单位:mm).电镀时,如果每平方米用锌0.1千克,电镀1000个这样的锚标浮筒,需要多少千克锌?(π的值取3.14)( )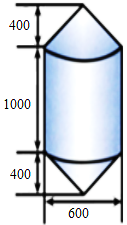 A、282.6 B、282600000 C、357.96 D、3579600006. 由4个棱长均为1的小正方形组成如图所示的几何体,这个几何体的表面积为( )
A、282.6 B、282600000 C、357.96 D、3579600006. 由4个棱长均为1的小正方形组成如图所示的几何体,这个几何体的表面积为( ) A、18 B、15 C、12 D、67. 正方体的每个面上都有一个汉字,如图是它的一种平面展开图,那么在原正方体中,与“盐”字所在面相对的面上的汉字是( )
A、18 B、15 C、12 D、67. 正方体的每个面上都有一个汉字,如图是它的一种平面展开图,那么在原正方体中,与“盐”字所在面相对的面上的汉字是( ) A、强 B、富 C、美 D、高8. 如图,已知骰子相对两面的点数之和为7,下列图形为该骰子表面展开图的是( )
A、强 B、富 C、美 D、高8. 如图,已知骰子相对两面的点数之和为7,下列图形为该骰子表面展开图的是( ) A、
A、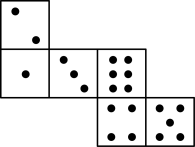 B、
B、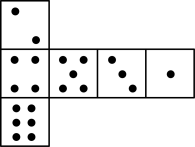 C、
C、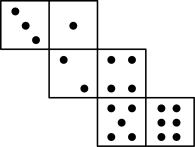 D、
D、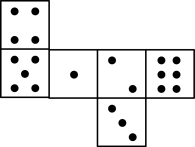 9. 如图,裁掉一个正方形后能折叠成正方体,但不能裁掉的是( )
9. 如图,裁掉一个正方形后能折叠成正方体,但不能裁掉的是( )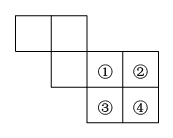 A、① B、② C、③ D、④10. 如图1所示,将长为6的矩形纸片沿虚线折成3个矩形,其中左右两侧矩形的宽相等,若要将其围成如图2所示的三棱柱形物体,则图中a的值可以是( )
A、① B、② C、③ D、④10. 如图1所示,将长为6的矩形纸片沿虚线折成3个矩形,其中左右两侧矩形的宽相等,若要将其围成如图2所示的三棱柱形物体,则图中a的值可以是( )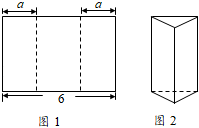 A、1 B、2 C、3 D、411. 下列图形中,为圆柱的侧面展开图的是( )A、
A、1 B、2 C、3 D、411. 下列图形中,为圆柱的侧面展开图的是( )A、 B、
B、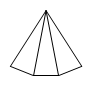 C、
C、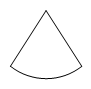 D、
D、 12. 如图为一个几何体的表面展开图,则该几何体是( )
12. 如图为一个几何体的表面展开图,则该几何体是( )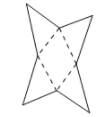 A、三棱锥 B、四棱锥 C、四棱柱 D、圆锥13. 某个立体图形的侧面展开图如图所示,它的底面是正三角形,那么这个立体图形是( )
A、三棱锥 B、四棱锥 C、四棱柱 D、圆锥13. 某个立体图形的侧面展开图如图所示,它的底面是正三角形,那么这个立体图形是( ) A、圆柱 B、圆锥 C、三棱柱 D、四棱柱14. 下列图形中,正方体展开图错误的是( )
A、圆柱 B、圆锥 C、三棱柱 D、四棱柱14. 下列图形中,正方体展开图错误的是( ) A、
A、 B、
B、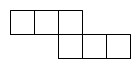 C、
C、 D、
D、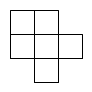 15. 如图为一个长方体的展开图,且长方体的底面为正方形.根据图中标示的长度,求此长方体的体积为何?( )
15. 如图为一个长方体的展开图,且长方体的底面为正方形.根据图中标示的长度,求此长方体的体积为何?( )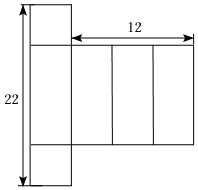 A、144 B、224 C、264 D、30016. 如图是某几何体的展开图,该几何体是( )
A、144 B、224 C、264 D、30016. 如图是某几何体的展开图,该几何体是( )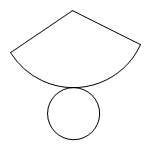 A、长方体 B、正方体 C、圆锥 D、圆柱17. 如图,用一个平行于圆锥底面的平面截圆锥,截面的形状是( )
A、长方体 B、正方体 C、圆锥 D、圆柱17. 如图,用一个平行于圆锥底面的平面截圆锥,截面的形状是( )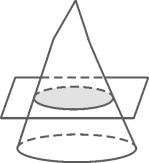 A、
A、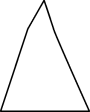 B、
B、 C、
C、 D、
D、
二、填空题(每题4分,共20分)
-
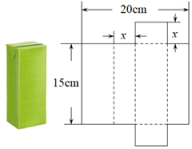
18. 已知Rt△ABC的两直角边AC=8,BC=6,将Rt△ABC绕AC所在的直线旋转一周形成的立体图形的侧面积为 (结果保留π).19. 将一个容积为360cm3的包装盒剪开铺平,纸样如图所示.利用容积列出图中x(cm)满足的一元二次方程:(不必化简).
 20. 如图是一个正方体的展开图,将它拼成正方体后,“神”字对面的字是.
20. 如图是一个正方体的展开图,将它拼成正方体后,“神”字对面的字是.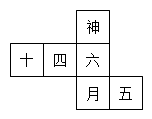 21. 在“抛掷正六面体”的试验中,正六面体的六个面分别标有数字“1”“2”“3”“4”“5”“6”,在试验次数很大时,数字“6”朝上的频率的变化趋势接近的值是.22. 如图,一个正方体由 27 个大小相同的小立方块搭成,现从中取走若干个小立方块,得到一个新的几何体.若新几何体与原正方体的表面积相等,则最多可以取走个小立方块.
21. 在“抛掷正六面体”的试验中,正六面体的六个面分别标有数字“1”“2”“3”“4”“5”“6”,在试验次数很大时,数字“6”朝上的频率的变化趋势接近的值是.22. 如图,一个正方体由 27 个大小相同的小立方块搭成,现从中取走若干个小立方块,得到一个新的几何体.若新几何体与原正方体的表面积相等,则最多可以取走个小立方块.
三、作图题(共2题,共20分)
-
23. 一个等腰 如图所示,将它绕直线AC旋转一周,形成一个几何体.
 (1)、写出这个几何体的名称,并画出这个几何体的三视图.(2)、依据图中的测量数据,计算这个几何体的表面积(结果保留π).24. 将立方体纸盒沿某些棱剪开,且使六个面连在一起,然后铺平,可以得到其表面展开图的平面图形.(1)、以下两个方格图中的阴影部分能表示立方体表面展开图的是(填A或B).
(1)、写出这个几何体的名称,并画出这个几何体的三视图.(2)、依据图中的测量数据,计算这个几何体的表面积(结果保留π).24. 将立方体纸盒沿某些棱剪开,且使六个面连在一起,然后铺平,可以得到其表面展开图的平面图形.(1)、以下两个方格图中的阴影部分能表示立方体表面展开图的是(填A或B).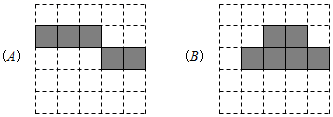 (2)、在以下方格图中,画一个与(1)中呈现的阴影部分不相似(包括不全等)的立方体表面展开图.(用阴影表示)
(2)、在以下方格图中,画一个与(1)中呈现的阴影部分不相似(包括不全等)的立方体表面展开图.(用阴影表示) (3)、如图中的实线是立方体纸盒的剪裁线,请将其表面展开图画在右图的方格图中.(用阴影表示)
(3)、如图中的实线是立方体纸盒的剪裁线,请将其表面展开图画在右图的方格图中.(用阴影表示)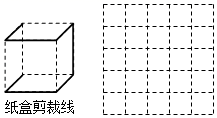
四、解答题(共3题,共26分)
-
25. 如图,用一个平面去截正方体ABCDEFGH,得到了三棱锥S﹣DPQ.若∠SPD=45°,∠SQD=37°,PQ=1,求SD的长.(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75.)
 26. 某工厂要加工一批上下底密封纸盒,设计者给出了密封纸盒的三视图,如图1.
26. 某工厂要加工一批上下底密封纸盒,设计者给出了密封纸盒的三视图,如图1. (1)、由三视图可知,密封纸盒的形状是;(2)、根据该几何体的三视图,在图2中补全它的表面展开图;(3)、请你根据图1中数据,计算这个密封纸盒的表面积.(结果保留根号)27. 数学学习小组的同学共同探究体积为330mL圆柱形有盖容器(如图所示)的设计方案.,他们想探究容器表面积与底面半径的关系.
(1)、由三视图可知,密封纸盒的形状是;(2)、根据该几何体的三视图,在图2中补全它的表面展开图;(3)、请你根据图1中数据,计算这个密封纸盒的表面积.(结果保留根号)27. 数学学习小组的同学共同探究体积为330mL圆柱形有盖容器(如图所示)的设计方案.,他们想探究容器表面积与底面半径的关系.
具体研究过程如下,请补充完整:
⑴建立模型:设该容器的表面积为S , 底面半径为cm,高为cm,则
, ①
, ②
由①式得 , 代入②式得
. ③
可知,S是x的函数,自变量x的取值范围是 .
⑵探究函数:
根据函数解析式③,按照下表中自变量x的值计算(精确到个位),得到了S与x的几组对应值:
…
1
1.5
2
2.5
3
3.5
4
4.5
5
5.5
6
…
…
666
454
355
303
277
266
266
274
289
310
336
…
在下面平面直角坐标系中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;

⑶解决问题:根据图表回答,
①半径为2.4cm的圆柱形容器比半径为4.4cm的圆柱形容器表面积 . (填“大”或“小”);
②若容器的表面积为300 , 容器底面半径约为cm(精确到0.1).