浙教版备考2023年中考数学一轮复习41.二次函数与不等式(组)
试卷更新日期:2022-12-31 类型:一轮复习
一、单选题(每题3分,共30分)
-
1. 一次函数y1=mx+n(m≠0)与二次函数y2=ax2+bx+c(a≠0)的图象如图所示,则不等式ax2+bx+c>mx+n的解集为( )
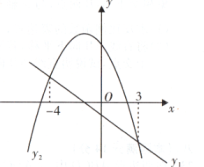 A、-4<x<3 B、x<-4 C、3-<<x<-4 D、x>3或x<-42. 如图,已知抛物线 与直线 交于 , 两点,则关于 的不等式 的解集是( )
A、-4<x<3 B、x<-4 C、3-<<x<-4 D、x>3或x<-42. 如图,已知抛物线 与直线 交于 , 两点,则关于 的不等式 的解集是( )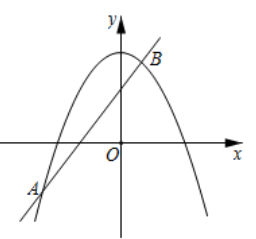 A、 或 B、 或 C、 D、3. 在研究函数图形的性质时,若将自变量x变为 , 则函数图象变化为:保留y轴右侧的图象,y轴左侧的图像变为右侧图象关于y轴的对称图形.已知抛物线y=-x2+2x+3的图象,则对于 , 当y>0时,x的取值范围是( )A、 B、 C、 D、4. 如图,抛物线关于直线对称,点在抛物线上,那么使得的x的取值范围是( )
A、 或 B、 或 C、 D、3. 在研究函数图形的性质时,若将自变量x变为 , 则函数图象变化为:保留y轴右侧的图象,y轴左侧的图像变为右侧图象关于y轴的对称图形.已知抛物线y=-x2+2x+3的图象,则对于 , 当y>0时,x的取值范围是( )A、 B、 C、 D、4. 如图,抛物线关于直线对称,点在抛物线上,那么使得的x的取值范围是( ) A、或 B、 C、 D、5. 如图,二次函数的图象的对称轴为x= , 且经过点(﹣2,0),(),(),下列说法正确的是( )
A、或 B、 C、 D、5. 如图,二次函数的图象的对称轴为x= , 且经过点(﹣2,0),(),(),下列说法正确的是( ) A、bc>0 B、当≥﹣时, C、a=2b D、不等式的解集是﹣2<x<6. 已知抛物线()与直线交于 , 两点,则关于的不等式的解集是( )A、或 B、或 C、 D、7. 如图,二次函数y=ax2+bx+c与反比例函数y=的图象相交于点A(﹣1,y1)、B(1,y2)、C(3,y3)三个点,则不等式ax2+bx+c>的解集是( )
A、bc>0 B、当≥﹣时, C、a=2b D、不等式的解集是﹣2<x<6. 已知抛物线()与直线交于 , 两点,则关于的不等式的解集是( )A、或 B、或 C、 D、7. 如图,二次函数y=ax2+bx+c与反比例函数y=的图象相交于点A(﹣1,y1)、B(1,y2)、C(3,y3)三个点,则不等式ax2+bx+c>的解集是( ) A、﹣1<x<0或1<x<3 B、x<﹣1或1<x<3 C、﹣1<x<0或x>3 D、﹣1<x<0或0<x<18. 在平面直角坐标系中,点 , 的坐标分别为 , ,若抛物线 与线段 有且只有一个交点,则 的值可以是( )A、 B、 C、1 D、9. 如图,抛物线y=ax2+bx+c与x轴交于两点(x1 , 0)、(2,0),其中0<x1<1.下列四个结论:①abc<0;②a+b+c>0;③2a﹣c>0;④不等式ax2+bx+c>﹣x+c的解集为0<x<x1.其中正确结论的个数是( )
A、﹣1<x<0或1<x<3 B、x<﹣1或1<x<3 C、﹣1<x<0或x>3 D、﹣1<x<0或0<x<18. 在平面直角坐标系中,点 , 的坐标分别为 , ,若抛物线 与线段 有且只有一个交点,则 的值可以是( )A、 B、 C、1 D、9. 如图,抛物线y=ax2+bx+c与x轴交于两点(x1 , 0)、(2,0),其中0<x1<1.下列四个结论:①abc<0;②a+b+c>0;③2a﹣c>0;④不等式ax2+bx+c>﹣x+c的解集为0<x<x1.其中正确结论的个数是( )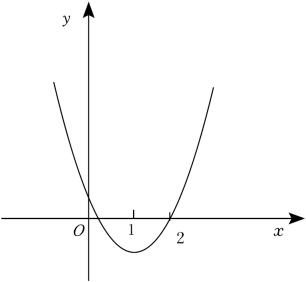 A、4 B、3 C、2 D、110. 已知 , 为抛物线 图象上的两点,且 ,则下列说法正确的是( )A、若 ,则 B、若 ,则 C、若 ,则 D、若 ,则
A、4 B、3 C、2 D、110. 已知 , 为抛物线 图象上的两点,且 ,则下列说法正确的是( )A、若 ,则 B、若 ,则 C、若 ,则 D、若 ,则二、填空题(每题4分,共24分)
-
11. 如图,直线y=kx+b与抛物线y=-x2+2x+3交于点A,B,且点A在y轴上,点B在x轴上,则不等式-x2+2x+3>kx+b的解集为 .
 12. 如图抛物线y=ax2与反比例函数交于点C(1,2),不等式的解集是 .
12. 如图抛物线y=ax2与反比例函数交于点C(1,2),不等式的解集是 .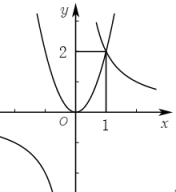 13. 如图,已知抛物线 与直线 交于 两点,则关于 的不等式 的解集是.
13. 如图,已知抛物线 与直线 交于 两点,则关于 的不等式 的解集是. 14. 抛物线 经过点 , 两点,则不等式 的解集是.15. 抛物线y=ax2+bx+c的部分图象如图所示,则不等式ax2+bx+c>0的解集为.
14. 抛物线 经过点 , 两点,则不等式 的解集是.15. 抛物线y=ax2+bx+c的部分图象如图所示,则不等式ax2+bx+c>0的解集为. 16. 已知抛物线 与 轴分别交于点 和 ,则不等式 的解集为 .
16. 已知抛物线 与 轴分别交于点 和 ,则不等式 的解集为 .三、解答题(共7题,共66分)
-
17. 自主学习,请阅读下列解题过程.
解一元二次不等式:x2﹣5x>0
解:设x2﹣5x=0,解得x1=0,x2=5,则抛物线y=x2﹣5x与x轴的交点坐标为(0,0)和(5,0).画出二次函数y=x2﹣5x的大致图象(如图所示),由图象可知:当x<0,或x>5时函数图象位于x轴上方,此时y>0,即x2﹣5x>0,所以,一元二次不等式x2﹣5x>0的解集为:x<0或x>5.

通过对上述解题过程的学习,按其解题的思路和方法解答下列问题:
(1)、一元二次不等式x2﹣5x<0的解集为.(2)、用类似的方法解一元二次不等式:x2﹣2x﹣3>0.18. 在平面直角坐标系xOy中,二次函数图象顶点为A,与x轴正半轴交于点B. (1)、求点B的坐标,并画出这个二次函数的图象;(2)、一次函数的图象过A,B两点,结合图象,直接写出关于x的不等式的解集.19. 抛物线的图象如图所示,根据图象回答问题.
(1)、求点B的坐标,并画出这个二次函数的图象;(2)、一次函数的图象过A,B两点,结合图象,直接写出关于x的不等式的解集.19. 抛物线的图象如图所示,根据图象回答问题. (1)、直接写出时,随的增大而;(2)、直接写出方程的根;(3)、直接写出不等式的解集;(4)、若方程没有实数根,直接写出的取值范围.20. 如图,二次函数 的图象与 轴交于点 ,点 在抛物线上,且与点 关于抛物线的对称轴对称,已知一次函数 的图象经过该二次函数图象上的点 及点 .
(1)、直接写出时,随的增大而;(2)、直接写出方程的根;(3)、直接写出不等式的解集;(4)、若方程没有实数根,直接写出的取值范围.20. 如图,二次函数 的图象与 轴交于点 ,点 在抛物线上,且与点 关于抛物线的对称轴对称,已知一次函数 的图象经过该二次函数图象上的点 及点 . (1)、求二次函数和点 的坐标;(2)、根据图象,写出满足 的 的取值范围.21. 在平面直角坐标系内,设二次函数y1=(x-a)2+a-1(a为常数).(1)、若函数y1的图象经过点(1,2),求函数y1的表达式.(2)、若函数y1的图象与一次函数y2=x+b(b为常数)的图象有且仅有一个交点,求b 的值.(3)、已知(m,n)( m>0)在函数y1的图象上,当m>2a时,求证:n>
(1)、求二次函数和点 的坐标;(2)、根据图象,写出满足 的 的取值范围.21. 在平面直角坐标系内,设二次函数y1=(x-a)2+a-1(a为常数).(1)、若函数y1的图象经过点(1,2),求函数y1的表达式.(2)、若函数y1的图象与一次函数y2=x+b(b为常数)的图象有且仅有一个交点,求b 的值.(3)、已知(m,n)( m>0)在函数y1的图象上,当m>2a时,求证:n>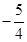 . 22. 某商场经营某种品牌的玩具,购进时的单价是30元,根据市场调查:在一段时间内,销售单价是40元时,销售量是600件,而销售单价每涨1元,就会少售出10件玩具。(1)、不妨设该种品牌玩具的销售单价为在40元的基础上上涨x(x>0),请你分别用x的代数式来表示销售量y件和销售该品牌玩具获得利润W(元),并把结果填写在表格中:
. 22. 某商场经营某种品牌的玩具,购进时的单价是30元,根据市场调查:在一段时间内,销售单价是40元时,销售量是600件,而销售单价每涨1元,就会少售出10件玩具。(1)、不妨设该种品牌玩具的销售单价为在40元的基础上上涨x(x>0),请你分别用x的代数式来表示销售量y件和销售该品牌玩具获得利润W(元),并把结果填写在表格中:销售单价(元)
40+x
销售量y(件)
销售玩具获得利润W(元)
(2)、在(1)问条件下,若商场获得10000元销售利润,则该玩具销售单价应定为多少元?(3)、在(1)问条件下,若玩具厂规定该品牌玩具销售单价不低于44元,且商场要完成不少于540件的销售任务,求商场销售该品牌玩具获得的最大利润是多少?23. 已知关于的函数.(1)、若 , 函数的图象经过点和点 , 求该函数的表达式和最小值;(2)、若 , , 时,函数的图象与轴有交点,求的取值范围.(3)、阅读下面材料:设 , 函数图象与轴有两个不同的交点 , , 若 , 两点均在原点左侧,探究系数 , , 应满足的条件,根据函数图象,思考以下三个方面:
①因为函数的图象与轴有两个不同的交点,所以;
②因为 , 两点在原点左侧,所以对应图象上的点在轴上方,即;
③上述两个条件还不能确保 , 两点均在原点左侧,我们可以通过抛物线的对称轴位置来进一步限制抛物线的位置:即需.
综上所述,系数 , , 应满足的条件可归纳为:
请根据上面阅读材料,类比解决下面问题:
若函数的图象在直线的右侧与轴有且只有一个交点,求的取值范围.