浙教版备考2023年中考数学一轮复习24.不等式及其性质

试卷更新日期：2022-12-31 类型：一轮复习

进入出卷网下载

一、单选题（每题3分，共30分）

1. 下列式子：①-2≤0；②3x+2y＞0；③b=2；④m≠3；⑤x+y；⑥x+5≤6是不等式的有（）

A、3个 B、4个 C、5个 D、6个

查看试题解析
2. 若 $x > y$ ，则下列式子中，不正确的是（）

A、 $x - 3 > y - 3$ B、 $x + 3 > y + 3$ C、 $- 3 x > - 3 y$ D、 $3 x > 3 y$

查看试题解析
3. 某不等式的解在数轴上表示如图，则该不等式的解是（）

A、 $x \leq 3$ B、 $x < 3$ C、 $x \geq 3$ D、 $x > 3$

查看试题解析
4. 如图，数轴上的点A和点B分别在原点的左侧和右侧，点A、B对应的实数分别是a、b，下列结论一定成立的是（）

A、 $a + b < 0$ B、 $b - a < 0$ C、 $2 a > 2 b$ D、 $a + 2 < b + 2$

查看试题解析
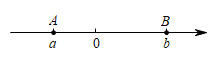5. 下列结论中，正确的是（）

A、若 $a > b$ ， $c \neq 0$ ，则 $a c > b c$ B、若 $a b < 0$ ，则 $a > 0$ ， $b < 0$ C、若 $a > 0$ ， $b < 0$ ，则 $a b < 0$ D、若 $\frac{a}{b} > 1$ ，则 $a > b$

查看试题解析
6. 如图，是关于x的不等式2x-m< -1的解集，则整数m的值为（）

A、 $m \leq - 2$ B、 $m \leq - 1$ C、 $m = - 2$ D、 $m = - 1$

查看试题解析
7. 已知a，b，c，d是实数，若a>b，c=d，则（）

A、a+c>b+d B、a+b>c+d C、a+c>b-d D、a+b>c-d

查看试题解析
8. 若 $x = 3.5$ 是某不等式的解，则该不等式可以是（）

A、 $x > 5$ B、 $x > 4$ C、 $x < 4$ D、 $x < 3$

查看试题解析
9. 若a，b，c，d为整数，且a＜2b，b＜3c，c＜4d，d＜100，则a可能取的最大值是（）

A、2367 B、2375 C、2391 D、2399

查看试题解析
10. 设m，n是实数，a，b是正整数，若 $(m + n) a ⩾ (m + n) b$ ，则（）

A、 $m + n + a ⩾ m + n + b$ B、 $m + n - a ⩽ m + n - b$ C、 $\frac{a}{m + n} ⩾ \frac{b}{m + n}$ D、 $\frac{m + n}{a} ⩽ \frac{m + n}{b}$

查看试题解析

二、填空题（每题4分，共24分）

11. 用不等式表示：x与y的和大于3 ．

查看试题解析
12. 武汉市某一天的最低气温为-6℃，最高气温是5℃，如果设这天气温为t℃，那么t应满足条件 .

查看试题解析
13. 若a＞b，且（6-x）a＜（6-x）b，则x的取值范围是.

查看试题解析
14. 已知 $a$ ， $b$ 是两个连续整数， $a < 2 - \sqrt{3} < b$ ，则 $a =$ ， $b =$ .

查看试题解析
15. 温故知新：若满足不等式 $\frac{8}{15} < \frac{n}{n + k} < \frac{7}{13}$ 的整数k只有一个，则正整数n的最大值．
阅读理解：任意正整数 $a$ ， $b$ ， ∵ ${(\sqrt{a} - \sqrt{b})}^{2} \geq 0$ ， ∴ $a - 2 \sqrt{a b} + b \geq 0$ ， ∴ $a + b ≥ 2 \sqrt{a b}$ ，只有当 $a = b$ 时，等号成立；结论：在 $a + b ≥ 2 \sqrt{a b}$ （ $a$ 、 $b$ 均为正实数）中，只有当 $a = b$ 时， $a + b$ 有最小值 $2 \sqrt{a b}$ ．若 $m > 1$ ， $\sqrt{m} + \frac{1}{\sqrt{m} - 1}$ 有最小值为．

查看试题解析
16. 在数学著作《算术研究》一书中，对于任意实数，通常用[x]表示不超过x的最大整数，如：[π]＝3，[2]＝2，[﹣2.1]＝﹣3．当﹣1＜x＜1时，[1+x]+[1﹣x]的值为．

查看试题解析

三、解答题（共8题，共66分）

17. 在公路上，同学们常能看到如图所示的几种不同交通标志图形，它们有着不同的意义，如果设汽车载重为x，速度为y，宽度为l，高度为h，请你用不等式表示图中各种标志的意义.

查看试题解析
18. 在不同的数轴上表示下列不等式，并分别写出满足不等式的所有负整数。

(1)、x＞ $-$ 2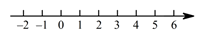

(2)、-2≤x＜1

查看试题解析
19. 现有不等式的两个性质：①在不等式的两边都加上(或减去)同一个数(或整式)，不等号的方向不变.②在不等式的两边都乘同一个数(或整式)，乘的数(或整式)为正时不等号的方向不变，乘的数(或整式)为负时不等号的方向改变.
请解决以下两个问题：

(1)、利用性质①比较2a 与a 的大小(a≠0).

(2)、利用性质②比较2a 与a 的大小(a≠0).

查看试题解析
20. 根据等式和不等式的基本性质，我们可以得到比较两数大小的方法：

(1)、若a-b＞0，则ab；

(2)、若a-b＝0，则ab；

(3)、若a-b＜0，则ab．

(4)、这种比较大小的方法称为“求差法比较大小”．
请运用这种方法尝试解决下面的问题：

比较4+3a²-2b+b²与3a²-2b+1的大小．

查看试题解析
21.

(1)、若a＜0，则a2a；（用“＞”“＜”“＝”填空）

(2)、若a＜c＜b＜0，则abc0；（用“＞”“＜”“＝”填空）

(3)、若a＜c＜0＜b，化简：4（c﹣a）﹣2（2c﹣b），并判断化简结果的正负．

查看试题解析
22.

(1)、若x＞y，比较﹣3x+5与﹣3y+5的大小，并说明理由；

(2)、若x＞y，且（a﹣3）x＜（a﹣3）y，求a的取值范围．

查看试题解析
23. 规定：用符号 $[x]$ 表示一个不大于实数x的最大整数，例如： $[3.69] = 3$ ， $[\sqrt{3} + 1] = 2$ ， $[- 2.56] = - 3$ ， $[- \sqrt{3}] = - 2$ ．按这个规定，求 $[- \sqrt{13} - 1]$ ．

查看试题解析